This document outlines trigonometric leveling and deriving equations to determine elevation differences between two stations using a single observation. It introduces determining elevation differences using angles of elevation or depression. Derivations show how horizontal distance, observed angle, and corrections for curvature, refraction and signal axis result in equations relating elevation difference to distance and corrected angle. Approximate expressions are also provided assuming a plane right angle at the observed point.

1. Advance Surveying
Trigonometric Leveling
Prof. Rajguru R.S.
Civil Engineering Department
(rajgururajeshcivil@sanjivani.org.in)
Sanjivani College of Engineering,
Kopargaon,MH,India

2. Lecture Outline
Determination of Difference in elevation by
single observation
 Introduction
 Equation to determine the difference in
Elevation

3.  Determination of Difference in elevation by single
observation:
• Introduction:
• Under many circumstances, it is not possible to occupy both the stations,
one of them being inaccessible, this method of determining the difference
in elevation between the two station is used.
• The vertical angle is corrected for curvature , refraction and axis signal
• Since the coefficient of refraction varies with temperature, this method does
not yield accurate results.

4.  Derivation of an Equation to determine the difference in Elevation
: (Angle of elevation)
• ∝ = Observed angle of elevation
• D = Horizontal distance = AA’
• ∝1 = Corrected vertical angle for axis
signal
• ∠B AA’ =α +(C - 𝛾) = α +
ᆈ
2
- m ᆈ
• ∠ AA’ B = ( 90° -
ᆈ
2
) + ᆈ = 90° +
ᆈ
2
• ∠ABA’ =180°-(α+
ᆈ
2
- m ᆈ )-(90° +
ᆈ
2
)
• = 90° - (α +ᆈ- m ᆈ )
Fig.3.1

5.  (Angle of elevation):
• Applying sine rule,
•
BA’
𝑠𝑖𝑛∠BAA’
=
AA’
𝑠𝑖𝑛∠ABA’
•
H
𝑠𝑖𝑛(α+ᆈ
2
− m ᆈ)
=
D
𝑠𝑖𝑛(90° −(α + ᆈ −m ᆈ))
• H = D
𝑠𝑖𝑛(α + ᆈ
2
− m ᆈ)
𝐶𝑂𝑆(α + ᆈ − m ᆈ)
• But, D = R ᆈ, ᆈ =
D
𝑅
=
D
𝑅𝑆𝑖𝑛1"
• H =D
𝑠𝑖𝑛(α + D
2𝑅𝑆𝑖𝑛1"
− 𝑚D
𝑅𝑆𝑖𝑛1"
)
𝐶𝑂𝑆(α + D
𝑅𝑆𝑖𝑛1"
− 𝑚D
𝑅𝑆𝑖𝑛1"
)
• H =D
𝑠𝑖𝑛(α + D
2𝑅𝑆𝑖𝑛1"
− 𝑚D
𝑅𝑆𝑖𝑛1"
)
𝐶𝑂𝑆(α + D
𝑅𝑆𝑖𝑛1"
− 𝑚D
𝑅𝑆𝑖𝑛1"
)
• H =D
𝑠𝑖𝑛 (α+(1 − 2m) D
2𝑅𝑆𝑖𝑛1"
)
𝐶𝑂𝑆 (α+(1−m) D
𝑅𝑆𝑖𝑛1"
)
• Eq. can be modified by butting α = α1
• Fig.3.1

6.  Derivation of an Equation to determine the difference in
Elevation : (Angle of depression):
• 𝛃 = Angle of depression at B
• 𝛃1 = Corrected vertical angle for axis
signal
• H= Difference in elevation
• ∠ABB’ = 𝛃 - C + 𝛾 = 𝛃 -
ᆈ
2
+ m ᆈ
• ∠ BB’A = ( 90° - ᆈ ) +
ᆈ
2
= 90° -
ᆈ
2
• ∠B’AB =180°-(90°-
ᆈ
2
)-(𝛃 -
ᆈ
2
+ m ᆈ)
• = 90° - (𝛃 - ᆈ + m ᆈ )
Fig:3.2

7.  (Angle of depression)::
• Applying sine rule, ΔBAB’
•
𝐴B’
𝑠𝑖𝑛∠ ABB’
=
𝐵𝐵’
𝑠𝑖𝑛∠B′AB
•
H
𝑠𝑖𝑛(𝛃−ᆈ
2
+ m ᆈ)
=
D
𝑠𝑖𝑛(90° −( 𝛃 − ᆈ + m ᆈ))
• H = D
𝑠𝑖𝑛( 𝛃 − ᆈ
2
+ m ᆈ)
𝐶𝑂𝑆( 𝛃 − ᆈ + m ᆈ)
• But, D = R ᆈ, ᆈ =
D
𝑅
=
D
𝑅𝑆𝑖𝑛1"
• H =D
𝑠𝑖𝑛(𝛃 − D
2𝑅𝑆𝑖𝑛1"
+ 𝑚D
𝑅𝑆𝑖𝑛1"
)
𝐶𝑂𝑆(𝛃 − D
𝑅𝑆𝑖𝑛1"
+
𝑚D
𝑅𝑆𝑖𝑛1"
)
• H =D
𝑠𝑖𝑛(𝛃 − D
2𝑅𝑆𝑖𝑛1"
+ 𝑚D
𝑅𝑆𝑖𝑛1"
)
𝐶𝑂𝑆(𝛃 − D
𝑅𝑆𝑖𝑛1"
+ 𝑚D
𝑅𝑆𝑖𝑛1"
)
• H =D
𝑠𝑖𝑛 (𝛃 −(1 − 2m) D
2𝑅𝑆𝑖𝑛1"
)
𝐶𝑂𝑆 (𝛃 −(1 − m) D
𝑅𝑆𝑖𝑛1"
)
• Eq. can be modified by butting 𝛃 = 𝛃1
Fig:3.2

8.  Approximate Expression: Assuming AA’B as a plane right angle
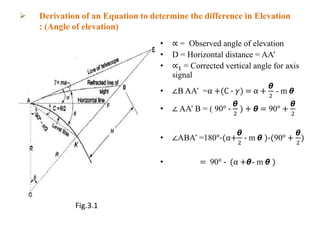
• α = Angle of elevation
• 𝛾 = Angle of refraction
• C = Angle of Curvature
• A’B = H = D tan Φ
• Φ = α +(C - 𝛾)
• H = D tan [α +(C - 𝛾) ]
• H = D tan [α +(
ᆈ
2
- m ᆈ)]
• H = D tan [α +( 1-2m)
𝐷
2𝑅𝑆𝑖𝑛1"
]
Expression for height difference
• 𝛃 = Angle of depression
• 𝛾 = Angle of refraction
• C = Angle of Curvature
• B’A = H = D tan Φ
• Φ = 𝛃 - C + 𝛾 = 𝛃 - (C - 𝛾)
• H = D tan [𝛃 - (C - 𝛾)]
• H = D tan [𝛃 - (
ᆈ
2
- m ᆈ)]
• H = D tan [𝛃 - ( 1-2m)
𝐷
2𝑅𝑆𝑖𝑛1"
]
• Expression for height difference

9. Thank you