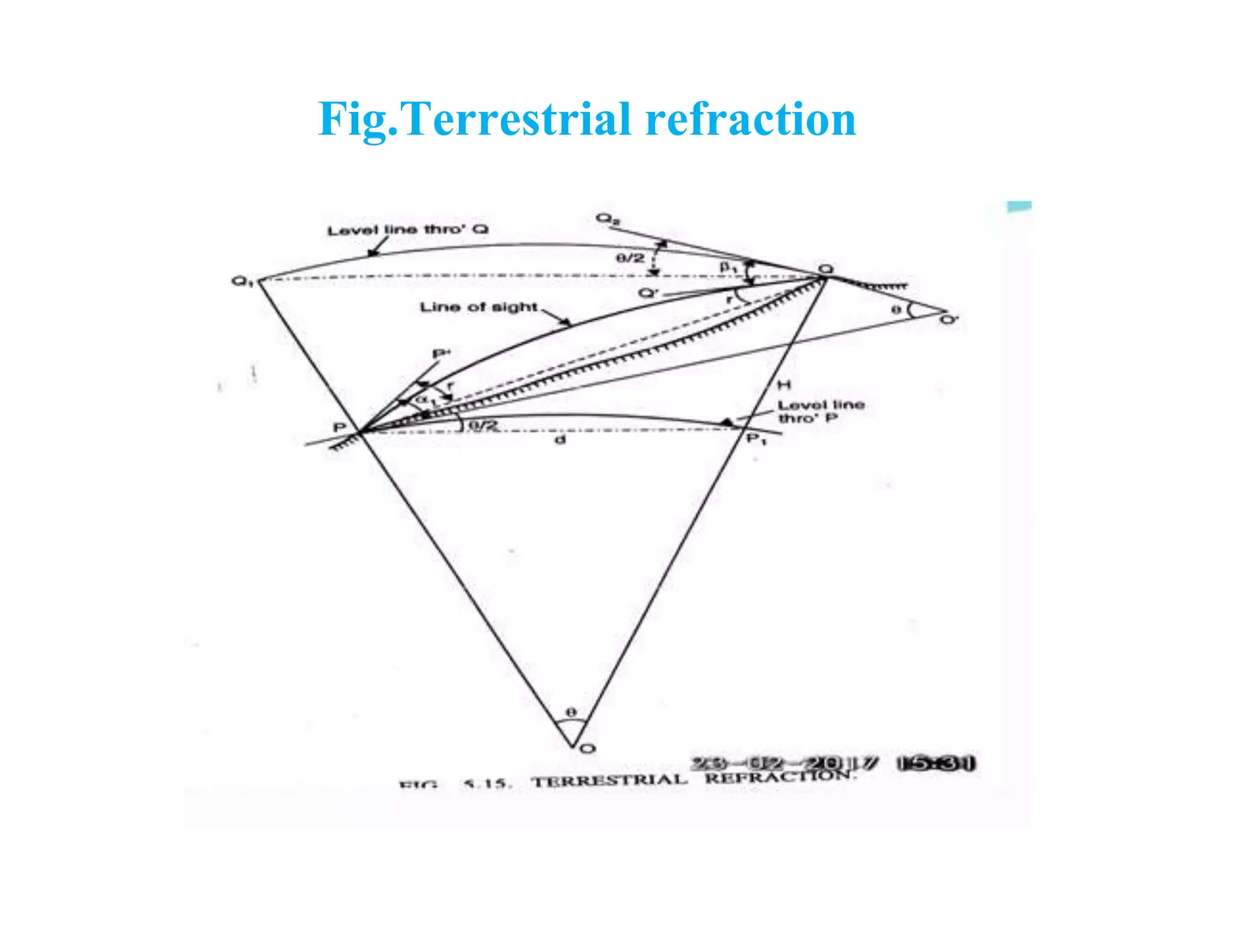
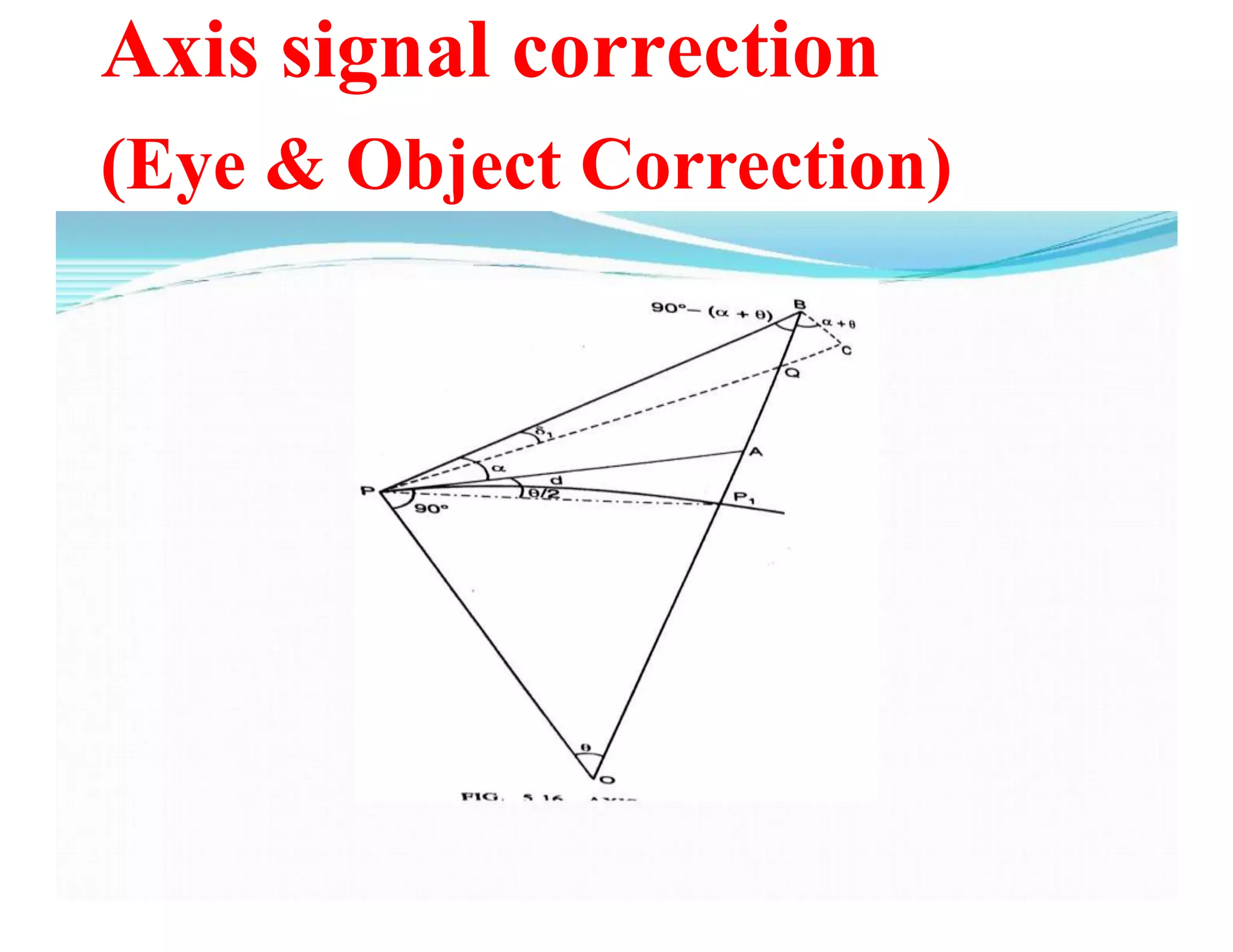
This document discusses methods of trigonometric leveling to determine elevation differences between points. It defines trigonometric leveling and describes corrections that must be applied for terrestrial refraction, curvature of the earth, and axis signal differences. The key methods discussed are determining elevation differences from a single observation using corrected angles of elevation or depression, and using reciprocal observations to eliminate refraction effects. Corrections are additive for depression angles and subtractive for elevation angles.

1. Advanced Surveying
Unit-6
Trignometric Levelling
Content
1. Trignometric Levelling
2. Terrestrial refraction,
3. Angular corrections for curvature and refraction,
4. Axis signal correction, Determination of difference in
elevation by single observation and reciprocal
observations.
Prepared by –Prof.S.M.Gunjal

2. Definition-Trignometric Levelling
 A method in which the relative elevation of different station are
found out from the measured vertical angle and known plane
horizontal distance or geodetic distance, is called as the
trigonometric levelling.

3. Terrestrial refraction
1. The effect of refraction is to make the object appear
higher than they really are in plan surveying where a
graduated staff isobserved either horizontal line of sight
or inclined line of sight ,the effect of refraction is to
decrease the staff reading and the correction is applied
linearly to the observed staff reading.
2. In trignometric levelling employed the elevation of
widely distributed points ,the correction is applied to the
observed angles.

4. Fig.Terrestrial refraction

5. P and Q are the two points the difference in elevation between
these being required .
Let,
O = centre of the earth
PO’ = tangent to the level line through P = horizontal line at P
QO’ = horizontal line at Q
<P’PO’ = α1 = observed angle of elevation from P to Q.
<Q’QQ2 = β1 = observed angle of depression from Q to P.
r = angle of refraction or angular correction for refraction
= <P’PQ
PP’ = tangent at P to the curve line of sight
PQ=apparent sight .
QQ’ = tangent at Q to the curved line of sight QP
=parent sight

6. d = horizontal distance between P and Q
R = mean radius of the earth = 6370 km
m = Co-efficient of refraction
Ɵ = angle subtended at the centre by distance PP1 over
which the observation are made.
The actual line of sight between P and Q should
have been along the straight line PQ but due to the
effect of the terrestrial refraction ,the actual line of
sight curved concave towards the ground surface .PP’
is,therefore the apparent sight from Q to P and QQ’
is the apparent from Q to P.since the angle are
measured on the circle of a theodolite ,they are
measured in the horizontal plane .

7. The angle measured at P towards Q is ,therefore ,the angle between the
apparent sight P’P and the horizontal line PQ’ hence <P’PO’ = observed
angle α1 ,the true angle elevation ,in the absence of refraction is
<P’PQ.calling this as r ,the correction is evidently subtractive
Thus ,correct angle = <QPO’ = < P’PQ = α1- r Similarly,the angle measured
at Q towards P is <Q’QQ= β1 .the true angle of depression . In the absence
of refraction is <PQQ2.
Hence the correction for refraction is <PQQ’ and be added to the observed
angle to get the correct angle.
Thus the correct angle = < PQQ2 = < Q’QQ2 + <Q’QP =
β1 +r
Thus the correction for the refraction is subtractive to the angle of
elevation and additive for the angle of
depression

8. Coefficient of refraction:-
The co-efficient of refraction (m) is the ratio
of the angle of refraction and the angle
subtended at the centre of the earth by the
distance over which observation are tken
Thus, m = r/Ɵ or r = m. Ɵ
The value of ‘m’ varies roughly between 0.06
to 0.08

9. Determination of correction refraction :-
In order to determine the angle of refraction r.
Case:-I : Distance ‘d’ small and ‘H’ large :-
r = ( Ɵ/2) – {(β1 – α 1) /2}
It assumed that the refraction error ‘r’ is the same at
both station
Writing r = m.Ɵ
and rearrange ,we get
2m Ɵ = Ɵ – (β1 - α 1 )
β1 = α 1 + Ɵ( 1- 2m)
Thus the observed angle of depression
Always exceed the angle of elevation by the amount Ɵ( 1- 2m)

10. Case :- II Distance ‘d’ large and ‘H’small:-
In this case ,both α 1 and β1 are the angle of
depression
Changing the sign of α 1 in equation
r = ( Ɵ/2) – {(β1 – α 1) /2}.
We get
r = ( Ɵ/2) – {(β1 + α 1) /2}
Which is reduce to: (β1 + α 1) = Ɵ (1 – 2m)

11. Correction for curvature:-
The correction for the curvature is
+Ɵ/2 for angle of elevation and
- Ɵ/2 for angle of depression.
Combined correction:-
Now,<O’PP1 = Ɵ/2 = d/ 2R radians
=( d/ 2R sin1”) seconds
Angular correction of refraction
= mƟ
= (m.d/ R sin1”) seconds

12. Hence , Combined angular correction
=[ (d/ 2R sin1”) –(m.d/ R sin1”) ]
= ( 1 – 2m ) d Seconds
2R sin1”
The combined correction is positive for angles
of elevation and negative for angle of
depression

13. Axis signal correction
(Eye & Object Correction)

14.  In order to observe the points from the
theodolite station .signals of appropriate
heights are erected at points to be observed
.The signal may or may not be same height
as that of the instrument .
 If height of the signal is not same as that of
the height of instrument axis above the
station , a correction known as the axis
signal correction or eye and object
correction is to be applied.

15. Let ,
h1= height of instrument at P,for observation to
Q.
h2 = height of instrument at Q,for bservation to
P.
s1 = height of instrument at P ,instrument being Q.
s2 = height of instrument at Q ,instrument being P.
d=horizontal distance between P and Q
α = Observed angle of elevation uncorrected for
the axis signal

16. β=Observed angle of depression uncorrected for
the axis signal.
α1= angle of elevation corrected for axis signal
β1=angle of depression corrected for axis signal.
In figure.
PA = horizontal line at P
Q= Point observed
BQ= difference in the height of signal at Q and
the height of instrument at P

17. = (s2-s1)
<BPA= α = angle observed from P to Q
<BPQ= δ1 = axis signal correction ( angular )at
P.
At B ,draw BC perpendicular to BP , to meet PQ
produce in C,

18. For triangle PBO
<BPO = <BPA + <APO = α + 900
<POB = Ɵ
<PBO = 180 – ( 90 + α ) – Ɵ
= 90 – (α + Ɵ)
<QBC = 90 – [ 90- (α + Ɵ)]
= (α + Ɵ)
The angle δ1 is usually very small and hence <BCQ can
be approximately taken equal to 900.
BC = BQ cos (α + Ɵ) very nearly
= (s2-h1)cos (α + Ɵ)] ………………………(1)

19. For triangle PP1B,
<BPP1= α + Ɵ/2
<PBP1= 90 – (α + Ɵ)
<PP1B = 180 –[ 90 - (α + Ɵ)]-(α +
Ɵ/2)
= (90 + Ɵ/2)
Now PB = PP1
sin PP1B sin PBP1
PB = [(d.sin (90 + Ɵ/2)]/[sin(90 – (α + Ɵ)]
= d.[ (cos Ɵ/2 ) / cos (α + Ɵ)]…………………..(2)

20. For triangle PBC,
Tanδ1 = BC
PB
Substituting the value of BC
from (1) & (2)
We get , Tanδ1 = (s2-h1)cos
(α + Ɵ)
d. (cos Ɵ/2 )
cos (α + Ɵ)
Tanδ1 = (s2-h1) cos (α + Ɵ)2
d .cos Ɵ/2 ………exactly

21. Usually Ɵ is small in comparison to α and may
be ignored
Tanδ1 = (s2-h1) cos α ……(a)2
d
The correction for signal evidently substrctive
for this case.
Similarly , if the if the observation are taken
from Q towards P ,it can be proved that
Tanδ2 = (s2-h1) cos β ( additive)2
d

22. The correction of axis signal is negative for angles of
elevation and positive for angle of depression .
If , however angle α or β is very small ,we can take ,with
sufficient accuracy
Tanδ1 = δ1 =( s2-h1) / d sin 1” seconds………….(b)
Tanδ2 = δ2 =( s2-h2) / d sin 1” ………………………(c)
By considering PB= PQ= PP1=d nd taking the arc with radius
equal to d. then
δ1 = [BQ/ d ]radians
= [( s2-h1) / d ]
= [( s2-h1) / d sin 1”] seconds

23.  This expression gives the sufficiently
accurate result when the vertical angle is
small , the difference is large and the
difference in height of the signal and that of
the instrument is small .after having
calculated δ1 & δ2 , The angle corrected for
the axis signal are given by
α1 ( elevation )= α - δ1
β1 ( Depression ) = β + δ2

24. DETERMINATION OF DIFFRENCE IN
ELEVATION:
The difference in elevation between the two points
P & Q can be found out by two method
(a) By single observation
(b) By reciprocal observation.
(a) By single observation:
The following correction will have to applied:
(1) Correction for Curvature.
(2) Correction for refraction.
(3) Correction for axis signal.

25. Since the sign of these correction will depend
upon the sign of the angle observed,
We shall consider following cases:
(i) When the observed angle is the angle of
elevation.
(ii) When the observed angle is the angle of
depression .

26. For angle of Elevation

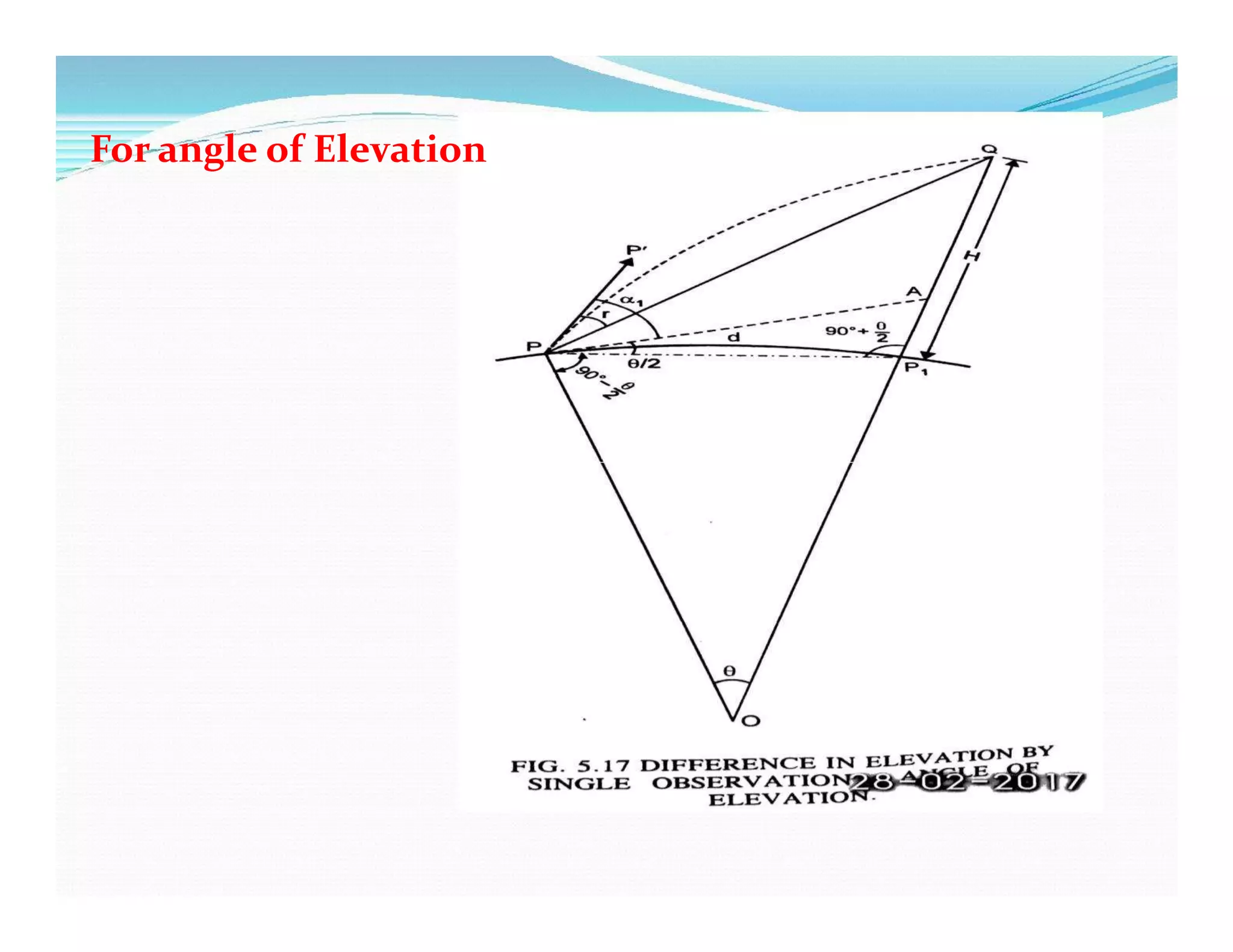
27. α = observed angle of elevation to Q
α1 = observed angle corrected for axis signal
= (α - δ1 )
= [α – (s2 –h1)/d sin 1”] seconds.
Therefore
QP1= d.sin α1+(m.d/Rsin1”) +(d/ 2R sin1”)
Cos α1+(m.d/Rsin1”) +(d/ 2R sin1”)

28. QP1= d.sin α1+(1-2m) (d/ 2R sin1”)
Cos α1+(1 – m) (d/ R sin1”)
Where the quantities (1-2m) (d/ 2R sin1”) and
(1 – m) (d/ R sin1”) are in seconds.
Approximate Expressions:
˂PP1Q= 90,Ѳ is very small
QP1 =H = PP1 tan QPP1= d tan [α1 - m Ѳ + Ѳ/2]
= d tan [α1 - (1-2m) (d/ 2R sin1”) ]

29. QP1= d.sin ᵝ1- (1-2m) (d/ 2R sin1”)
Cos ᵝ1 - (1 – m) - (d/ R sin1”)
Approximate Expression
˂ PQ1Q to be equal to 90 when Ѳ is very small
.Then
Q1P =H=QQ1 tan PQQ1=

30. For angle of depression

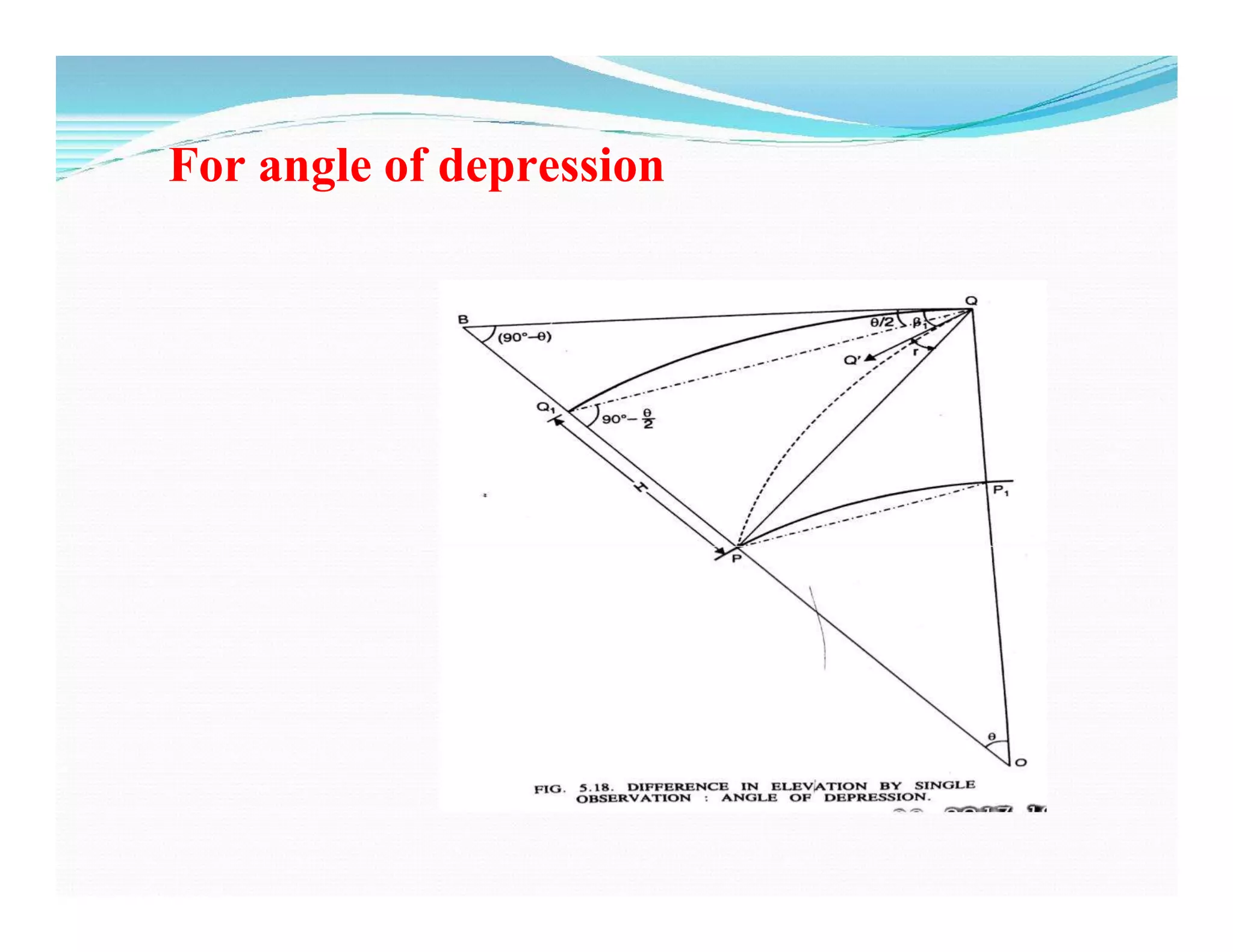
31. ᵝ = observed angle of depression to P
ᵝ1 = observed angle corrected for axis signal
= ᵝ + δ2
= [ᵝ – (s1 –h2)/d sin 1”] seconds
d = horizontal distance =
arc QQ1 = chord QQ1= QB

32. ᵝ = observed angle of depression to P
ᵝ1 = observed angle corrected for axis signal
= ᵝ + δ2
= [ᵝ – (s1 –h2)/d sin 1”] seconds
d = horizontal distance =
arc QQ1 = chord QQ1= QB
= d tan [ᵝ1 - (1-2m) (d/ 2R sin1”) ]

33. Difference in elevation by
Reciprocal :-
Reciprocal observation are generally
made to eliminate the effect of
refraction. in this method ,observation
are made simultaneously from both
station ( i.e P and Q )

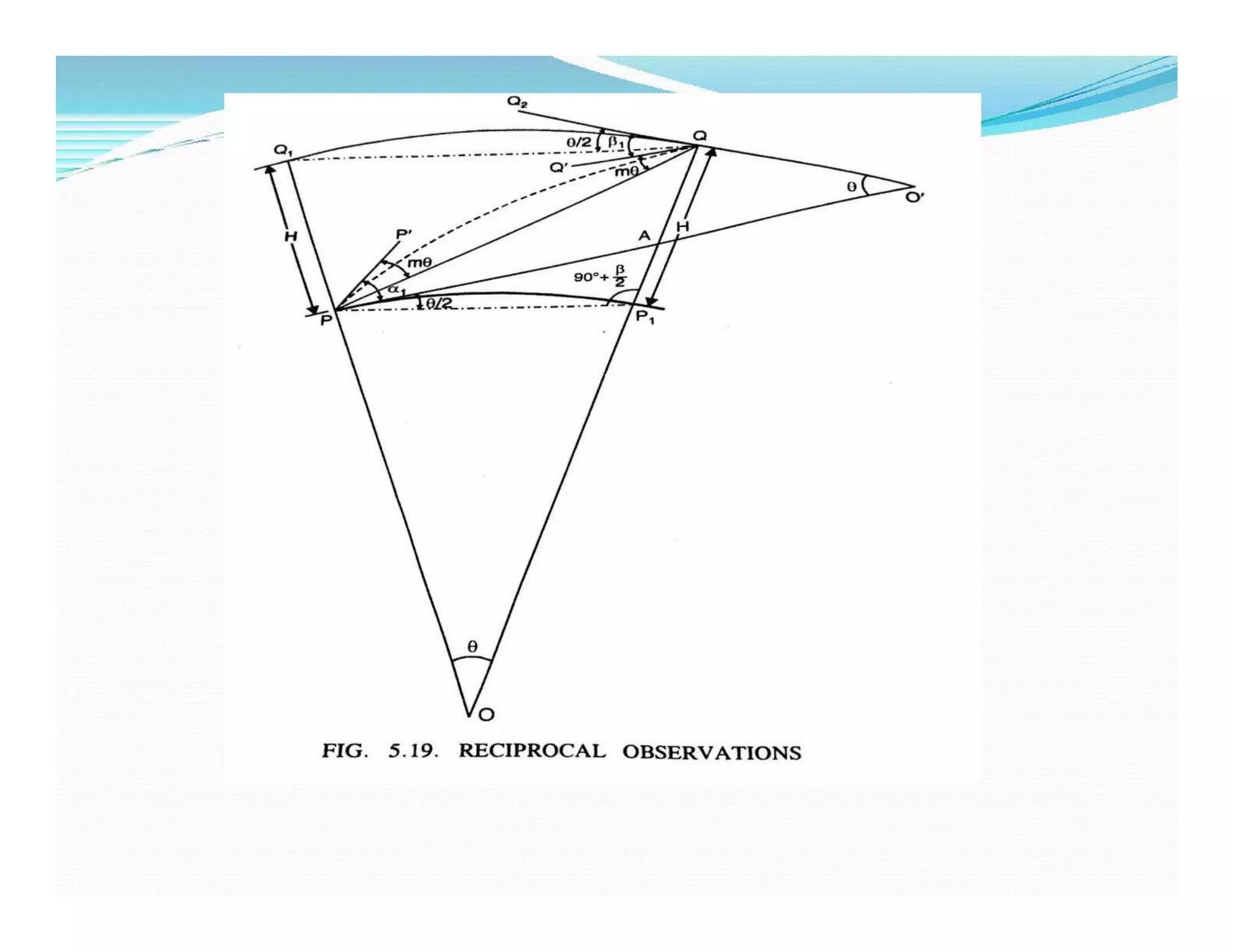
35. Both α1 and β1 are the angle of
depression ,the expression for H can
be obtained by changing the sign of
α1 .
H = d sin[ (β1 - α1 )/2]
cos [(β1 - α1 )/2 +Ɵ/2]