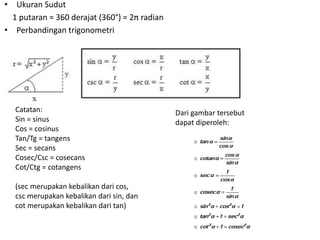
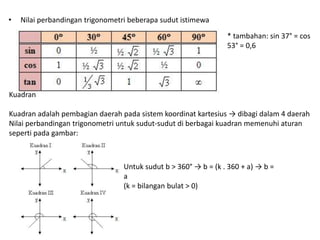
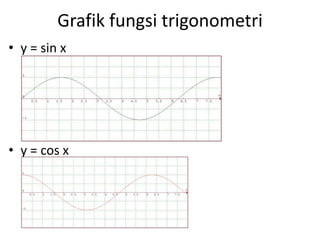
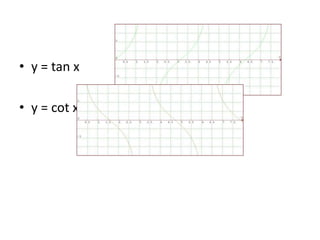
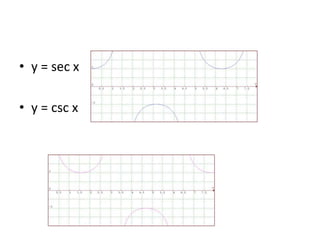
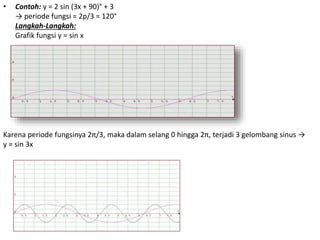
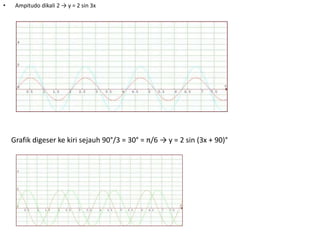
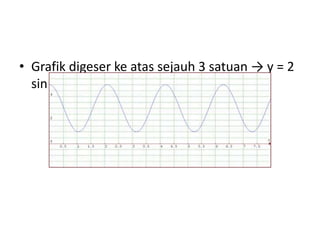
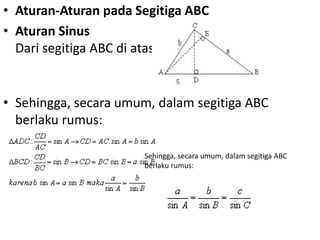
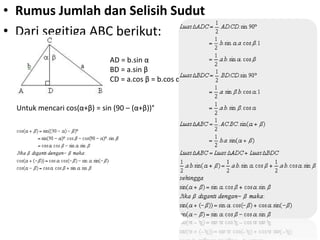
Dokumen ini membahas tentang trigonometri, termasuk ukuran sudut, perbandingan trigonometri, aturan sinus dan cosinus, serta grafik fungsi trigonometri. Selain itu, terdapat penjelasan mengenai sudut istimewa, identitas trigonometri, dan rumus-rumus terkait segitiga. Dokumen ini memberikan contoh soal dan cara menggambar grafik fungsi trigonometri.

1. Trigonometri
BAB 8

2. • Ukuran Sudut
1 putaran = 360 derajat (360°) = 2π radian
• Perbandingan trigonometri
Catatan:
Sin = sinus
Cos = cosinus
Tan/Tg = tangens
Sec = secans
Cosec/Csc = cosecans
Cot/Ctg = cotangens
(sec merupakan kebalikan dari cos,
csc merupakan kebalikan dari sin, dan
cot merupakan kebalikan dari tan)
Dari gambar tersebut
dapat diperoleh:

3. • Contoh:
• Dari segitiga berikut ini:
• Diketahui panjang AB = 12 cm, AC = 13 cm. Hitung semua nilai perbandingan
trigonometri untuk sudut A!
• Pertama, hitung dulu panjang BC dengan menggunakan rumus Phytagoras:

4. • A. Bentuk Umum B. Sudut-Sudut Istimewa
C. Hubungan Sudut Berelasi antara Sin, Cos dan
Tangen

5. D. Rumus-rumus Trigonometri
• 1. Aturan sinus
• 2. Aturan Cosinus
• 3. Luas Segitiga ABC
• 4. Jumlah dan Selish Dua Sudut

6. • 5. Sudut 2A (Sudut Kembar) 7. Jumlah Selisih Dua Fungsi Trigonometri
• 6. Hasil Kali Dua Fungsi Trigonometri 8. Persamaan Trigonometri
• 9. Bentuk a Cos x + b Sin x
• 10. Bentuk a Cos x + b Sin x = c
• 11. Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x

7. • Nilai perbandingan trigonometri beberapa sudut istimewa
* tambahan: sin 37° = cos
53° = 0,6
Kuadran
Kuadran adalah pembagian daerah pada sistem koordinat kartesius → dibagi dalam 4 daerah
Nilai perbandingan trigonometri untuk sudut-sudut di berbagai kuadran memenuhi aturan
seperti pada gambar:
Untuk sudut b > 360° → b = (k . 360 + a) → b =
a
(k = bilangan bulat > 0)

8. Mengubah fungsi trigonometri suatu sudut ke sudut lancip
Jika menggunakan 90 ± a atau 270 ± a maka fungsi berubah:
sin ↔ cos
tan ↔ cot
sec ↔ csc
Jika menggunakan 180 ± a atau 360 ± a maka fungsi tetap
Sudut dengan nilai negatif
Nilai negatif diperoleh karena sudut dibuat dari sumbu x, diputar searah jarum jam
Untuk sudut dengan nilai negatif, sama artinya dengan sudut yang berada di kuadran IV
Contoh:
Cos 120º = cos (180 – 60)º = – cos 60º = – 1/2 (120º ada di kuadran II sehingga nilai cos-nya negatif)
Cos 120º = cos (90 + 30)º = – sin 30º = – 1/2
Tan 1305º = tan (3.360 + 225)º = tan 225º = tan (180 + 45)º = tan 45º = 1 (225º ada di kuadran III
sehingga nilai tan-nya positif)
Sin –315º = – sin 315º = – sin (360 – 45)º = –(– sin 45)º = sin 45º = 1/2 √2

9. • Identitas Trigonometri
• Sehingga, secara umum, berlaku:
• sin2a + cos2a = 1
• 1 + tan2a = sec2a
• 1 + cot2a = csc2a

10. Grafik fungsi trigonometri
• y = sin x
• y = cos x

11. • y = tan x
• y = cot x

12. • y = sec x
• y = csc x

13. Menggambar Grafik fungsi y = A sin/cos/tan/cot/sec/csc (kx ± b) ± c
• Periode fungsi untuk sin/cos/sec/csc = 2π/k → artinya: grafik akan
berulang setiap kelipatan 2π/k
Periode fungsi untuk tan/cot = π/k → artinya: grafik akan berulang
setiap kelipatan π/k
• Nilai maksimum = c + |A|, nilai minimum = c – |A|
• Amplitudo = ½ (ymax – ymin)
• Cara menggambar:
Gambar grafik fungsi dasarnya seperti pada gambar di atas
Hitung periode fungsi, dan gambarkan grafik sesuai dengan periode
fungsinya
Jika A ≠ 1, kalikan semua nilai y pada grafik fungsi dasar dengan A
Untuk kx + b → grafik digeser ke kiri sejauh b/k
Untuk kx – b → grafik digeser ke kanan sejauh b/k
Untuk + c → grafik digeser ke atas sejauh c
Untuk – c → grafik digeser ke bawah sejauh c

14. • Contoh: y = 2 sin (3x + 90)° + 3
→ periode fungsi = 2p/3 = 120°
Langkah-Langkah:
Grafik fungsi y = sin x
Karena periode fungsinya 2π/3, maka dalam selang 0 hingga 2π, terjadi 3 gelombang sinus →
y = sin 3x

15. • Ampitudo dikali 2 → y = 2 sin 3x
Grafik digeser ke kiri sejauh 90°/3 = 30° = π/6 → y = 2 sin (3x + 90)°

16. • Grafik digeser ke atas sejauh 3 satuan → y = 2
sin (3x + 90)° + 3

17. • Aturan-Aturan pada Segitiga ABC
• Aturan Sinus
Dari segitiga ABC di atas:
• Sehingga, secara umum, dalam segitiga ABC
berlaku rumus:
Sehingga, secara umum, dalam segitiga ABC
berlaku rumus:

18. • Aturan Cosinus
• Dari segitiga ABC di atas:
•
• Sehingga, secara umum:
•
Luas Segitiga
Dari segitiga ABC di atas diperoleh:
Sehingga, secara umum:
• Sehingga secara umum

19. • Rumus Jumlah dan Selisih Sudut
• Dari segitiga ABC berikut:
AD = b.sin α
BD = a.sin β
CD = a.cos β = b.cos α
Untuk mencari cos(α+β) = sin (90 – (α+β))°

20. • Untuk fungsi tangens:
Sehingga, rumus-rumus yang diperoleh adalah:

21. Rumus Sudut Rangkap
Sehingga, rumus-rumus yang diperoleh adalah:
Penurunan dari rumus cos2α:

22. Rumus Perkalian Fungsi Sinus dan Kosinus
Dari rumus-rumus jumlah dan selisih dua sudut dapat diturunkan rumus-rumus
baru sebagai berikut:
Sehingga, rumus-rumus yang diperoleh:

23. • Rumus Jumlah dan Selisih Fungsi Sinus dan Kosinus
• Dari rumus perkalian fungsi sinus dan kosinus dapat diturunkan rumus
jumlah dan selisih fungsi sinus dan kosinus.
Maka akan diperoleh rumus-rumus:

24. Contoh-contoh soal:
(1) Tanpa menggunakan daftar, buktikan bahwa:

25. (2) Buktikan bahwa dalam segitiga ABC
berlaku: