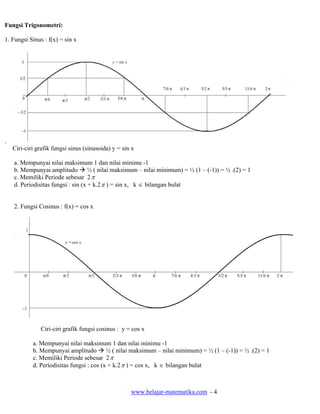
1. Dokumen tersebut membahas tentang trigonometri, termasuk pengertian sinus, cosinus, dan tangen, rumus-rumus penjumlahan dan pengurangan, rumus sudut rangkap, hubungan fungsi trigonometri, dan grafik fungsi trigonometri.
2. Dijelaskan pula hubungan koordinat cartesius dan koordinat kutub, nilai maksimum dan minimum, serta persamaan dan pertidaksamaan trigonometri.
3. Fungsi-fungsi trigonometri sepert