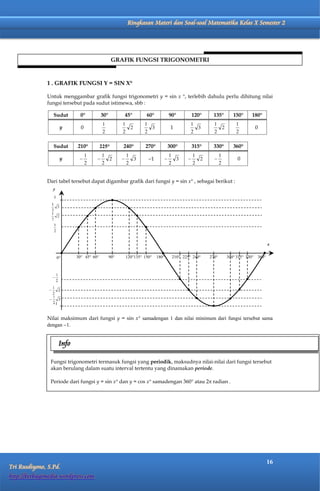
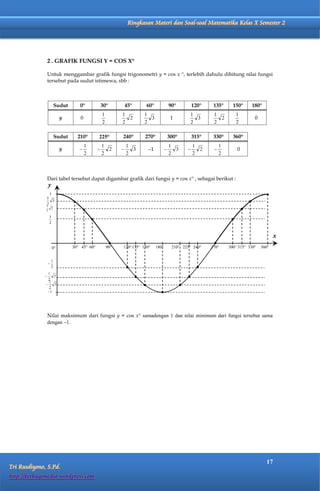
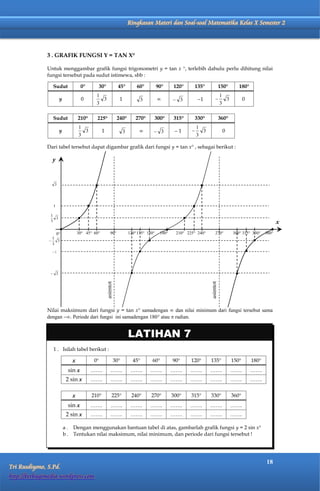
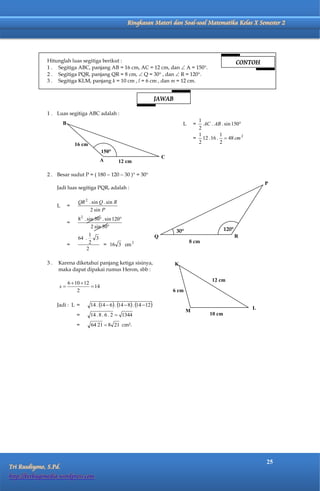
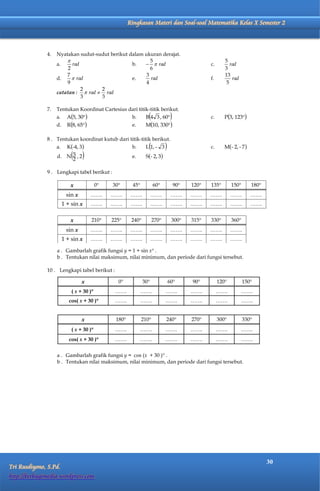
Dokumen ini membahas perbandingan trigonometri dalam segitiga siku-siku dan memberikan berbagai contoh serta latihan terkait perhitungan nilai sinus, kosinus, tangen, dan cotangen dari sudut-sudut tertentu. Selain itu, dokumen ini menjelaskan sistem koordinat kartesius dan kutub, serta bagaimana mengubah titik antara kedua sistem tersebut. Terdapat juga tabel perbandingan trigonometri untuk sudut-sudut istimewa dan informasi mengenai kuadran serta sifat perbandingan trigonometri di masing-masing kuadran.