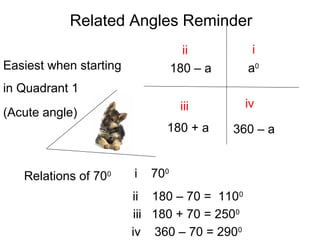
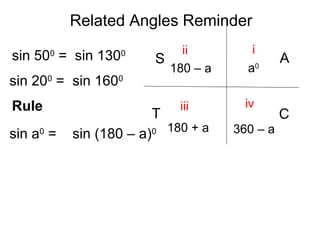
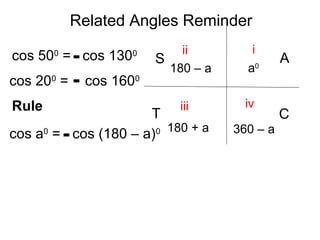
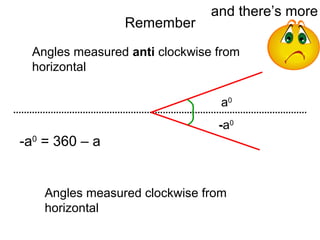
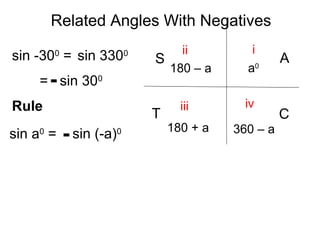
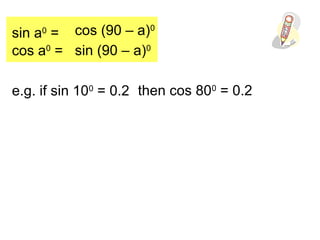
This document discusses trigonometric relationships between related angles. It contains the following rules: 1) sin(a) = sin(180 - a) and cos(a) = cos(180 - a), meaning trig functions of complementary angles are equal. 2) sin(a) = sin(-a) and cos(a) = cos(-a), meaning trig functions of coterminal angles are equal. 3) sin(a) = cos(90 - a) and cos(a) = sin(90 - a), relating trig functions that are 90 degrees out of phase.

1. Block 2
Trig Relationships

2. What is to be learned?
• How to use related angles to come up with
some pretty interesting rules (not!)

3. Related Angles Reminder
a0
180 – a
180 + a 360 – a
iii
iii iv
Easiest when starting
in Quadrant 1
(Acute angle)
Relations of 700 i 700
ii 180 – 70 = 1100
iii 180 + 70 = 2500
iv 360 – 70 = 2900

4. Related Angles Reminder
a0
180 – a
180 + a 360 – a
iii
iii iv
AS
T C
sin 500
= sin 1300
sin 200
= sin 1600
Rule
sin a0
= sin (180 – a)0

5. Related Angles Reminder
a0
180 – a
180 + a 360 – a
iii
iii iv
AS
T C
cos 500
= cos 1300
cos 200
= cos 1600
Rule
cos a0
= cos (180 – a)0
-
-
-

6. Remember
Angles measured anti clockwise from
horizontal
a0
Angles measured clockwise from
horizontal
-a0
-a0
= 360 – a
and there’s more

7. Related Angles With Negatives
a0
180 – a
180 + a 360 – a
iii
iii iv
AS
T C
sin -300
= sin 3300
= sin 300
Rule
sin a0
= sin (-a)0
-
-

8. Related Angles With Negatives
a0
180 – a
180 + a 360 – a
iii
iii iv
AS
T C
cos -400
=cos 3200
= cos 400
Rule
cos a0
= cos (-a)0

9. 0000
303000
454500
606000
909000
sin
cos
tan
0 π
/2
π
/3
π
/4
π
/6
degrees
rads
0 1½ 1
/√2
√3
/2
1 √3
/2
1
/√2 ½ 0
0 1
/√3 1 √3 ∞
Remember These?

10. 0000
303000
454500
606000
909000
sin
cos
tan
0 π
/2
π
/3
π
/4
π
/6
degrees
rads
0 1½ 1
/√2
√3
/2
1 √3
/2
1
/√2 ½ 0
0 1
/√3 1 √3 ∞
And Finally
Rule
sin a0
= cos (90 – a)0
Hang on in there…

11. Some Exciting Trig Rules
sin a0
= sin (180 – a)0
cos a0
= cos (180 – a)0-
e.g. if sin 400
= 0.6 then sin 1400
= 0.6
if cos 400
= 0.8 then cos1400
= 0.8
sin a0
= sin (- a)0
cos a0
= cos (- a)0
-
e.g. if sin 200
= 0.3 then sin (-20)0
= 0.3
e.g. if cos 200
= 0.9 then cos(-20)0
= 0.9
-
-

12. sin a0
= cos (90 – a)0
e.g. if sin 100
= 0.2 then cos 800
= 0.2
cos a0
= sin (90 – a)0

13. Key Question
Simplify cos(π
/2 – θ) + sin(-θ)
= sin θ – sin θ
= 0