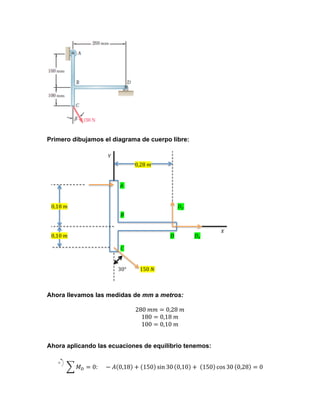
1) The document describes solving static equilibrium equations to analyze a lever system with forces applied. 2) Key values are calculated, such as the tension force TAB equals 300 N. 3) The normal and tangential force components Cx and Cy are calculated to be -380 N and -240 N, respectively.

1. Primero dibujamos el diagrama de cuerpo libre:
!
0,28!!
!!
0,18!!
!!
!
0,10!!
!
!
!
30°
150!!
Ahora llevamos las medidas de mm a metros:
ne Solutions Manual Organization System
280 𝑚𝑚 = 0,28 𝑚
180 = 0,18 𝑚
100 = 0,10 𝑚
on 19.
m:
!!
Ahora aplicando las ecuaciones de equilibrio tenemos:
(a) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝑀! = 0: − 𝐴 0,18 + 150 sin 30 0,10 + 150 cos 30 0,28 = 0
∴ TAB = 300
(b) From free-body diagram of lever BCD
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
∴ C x = −380 N
or
C x = 380 N

2. 21.
OS: Complete Online Solutions Manual Organization System
COSMOS: Complete Online Solutions Manual Organization System
pter 4, Solution 19.
𝑨 =
Chapter 4, Solution 19.
e-Body Diagram:
150 sin 30 0,10 + 150 cos 30 0,28
= 𝟐𝟒𝟑, 𝟕𝟒 𝑵
0,18
(a) From free-body diagram of lever BCD
Free-Body Diagram:
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
(a) From free-body 𝑜 𝑨lever𝟐𝟒𝟒 𝑵 →
diagram of = BCD
∴ TAB = 300
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
⎛ 2.4 in. ⎞
(b) From
−⎜
⎟ A − (0.9 in.)Fsp = 0 free-body diagram of lever BCD
Βx = 0 :
⎝ cosα ⎠
∴ T = 300
ΣFx = 0: 0: 243,74 +300 N ) = 0 30 + 𝐷 = 0 AB
𝐹! = 200 N + Cx + 0.6 ( 150 sin
!
8
(b) From free-body diagram of lever BCD
Fsp =
lb = kx = k (1.2 in.)
∴ C x = −380 N
or
C x = 380 N
cos 30°
ΣFx = 0: 200 N + C + 0.6 ( 300 N ) = 0
𝑫 𝒙 = 0: C y + − 150 xsin 30
ΣFy= −243,74 0.8 ( 300 N ) = 0 = −𝟑𝟏𝟖, 𝟕𝟒 𝑵
∴ C x = −380 N
or
k = 7.69800 lb/in.
k = 7.70 lb/in. ▹ C x = 380 N
∴ C y = −240 N
or
C y = 240 N
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
or
Then
8 lb ⎞
( 3 lb ) sin 30° + Bx + ⎛
⎜
⎟=0
⎝ cos30° ⎠
and Then
Bx = −10.7376 lb
0:
− ( 3 lb ) cos 30° + B y = 0
0:
C =
𝐹! = 0: 𝐷2 − 150 cos 30 = 0
!
2
2
2
C x + C y C = 380 ) N ( 240 ) = 449.44240 N
∴ = y ( −240 +
or
Cy = N
C
𝑫 ⎛ = ⎞ 150 cos 30 = 𝟏𝟐𝟗, 𝟗𝟎𝟒 𝑵
2
2
− 240 ⎞
2
C 1 y 2 = C y =⎛
) 32240 )
θ = tan −=𝒚⎜ C x⎟ + tan −1 ⎜ ( 380⎟ =+ ( .276° = 449.44 N
⎜C ⎟
⎝ − 380 ⎠
⎠
⎛ Cy ⎞
⎛ − 240 ⎞ C = 449 N
or = 32.276°
32.3° ▹
and
θ = tan −1 ⎜ ⎟ = tan −1 ⎜
⎟
⎜ C!⎟
!
⎝ − 380 ⎠ ! + 129,904 ! = 𝟑𝟒𝟒, 𝟐𝟎 𝑵
x ⎠
By = 2.5981 lb 𝑃𝑜𝑟 𝑙𝑜 𝑡𝑎𝑛𝑡𝑜: 𝑫 = 𝐷! + ⎝ 𝐷! = −318,74
or
or C = 449 N
32.3° ▹
2
2
= ( −10.7376 ) + ( 2.5981) = 11.0475 lb, and
𝐷
129,904
2.5981
= tan −1
= 13.6020°
10.7376
⎝
x
𝑎𝑑𝑒𝑚𝑎𝑠 𝜽 = tan!!
!
𝐷!
= tan!!
B 𝟑𝟒𝟒 𝑵
𝑜 𝑫 = = 11.05 lb
s: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
Clausen, David Mazurek, Phillip J. Cornwell
mpanies.
Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
7 The McGraw-Hill Companies.
Vector Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
Elliot R. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
© 2007 The McGraw-Hill Companies.
−318,74
13.60° 𝟐𝟐, 𝟐°
𝜽= ▹
= −𝟐𝟐, 𝟏𝟕𝟒°

3. Primero dibujamos el diagrama de cuerpo libre:
!!
!!
2!
+
!
os
!c
!!
!
!!
!
!!
!!
!!
!!
OS: Complete Online Solutions Manual Organization System
!
!
pter 4, Solution 19.
e-Body Diagram:
Ahora aplicando las ecuaciones de equilibrio tenemos:
(a) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝑀! = 0: 𝑇 2𝑎 + 𝑎 cos 𝜃 − 𝑇𝑎 + 𝑃𝑎 = 0
∴ TAB = 300
(b) From free-body diagram of lever BCD
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
∴ C x = −380 N
or
C x = 380 N
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
∴ C = −240 N
or
C = 240 N

4. Chapter 4, Solution 19.
Free-Body Diagram:
(a) From free-body diagram of lever BCD
𝑷
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝑻=
𝟏 + 𝐜𝐨𝐬 𝜽
(𝐼)
∴ TAB = 300
(b) From free-body diagram of lever BCD
ΣFx = 0: 0: 𝐶 x− 0.6 ( 300 = )0= 0
𝐹! = 200 N + C + 𝑇 sin 𝜃 N
!
∴ C x = −380 N
or
C x = 380 N
COSMOS: Complete Online Solutions Manual Organization System
𝑪 = C + 0.8 ( 300 N )
ΣFy = 𝒙0: 𝑻y 𝐬𝐢𝐧 𝜽 (𝐼𝐼) = 0
∴ C y = −240 N
C y = 240 N
or
De (I)
2
2
Chapter 4, Solution 19. en (II) se tiene que: C = Cx + C y = ( 380 )2 + ( 240 )2 = 449.44 N
Then
Free-Body Diagram:
𝑷 𝐬𝐢𝐧 𝜽
⎛C ⎞
⎛ − 240 ⎞
y
𝑪𝒙 =
θ = tan −1 ⎜ ⎟ = tan −1 (𝐼𝐼𝐼)= 32.276°
⎜ 𝟏 +⎟ 𝐜𝐨𝐬 𝜽 ⎜ − 380 ⎟
⎠
⎝
⎝ Cx ⎠
(a) From free-body diagram of lever BCD
and
or C = 449 N
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝐹! = 0: 𝐶! + 𝑇 + 𝑇 cos 𝜃 − 𝑃 = 0
32.3° ▹
∴ TAB = 300
(b) From free-body diagram of lever BCD
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
𝑪 𝒚 = 𝑷 − 𝑻 𝟏 + 𝐜𝐨𝐬 𝜽 (𝐼𝑉)
∴ C x = −380 N
C x = 380 N
or
ΣFy
De (I) en (IV) se tiene que:= 0: C y + 0.8 ( 300 N ) = 0
∴ C y = −240 N
C y = 240 N
or
Then
2
2
2
C = 𝐶C x= 𝑃y− 𝑃 ( 380 )cos (𝜃 = 0= 449.44 N
+ C 2 = 1 + + 240 )
!
and
⎛ Cy ⎞
⎛ − 240 ⎞
θ = tan ⎜ ⎟ = tan −1 ⎜
⎟
⎟
⎜ 𝑪 𝒚 = 𝟎 , 𝐶 = =!32.276°
⎝ − 380 ⎠ 𝐶
⎝ Cx ⎠
1 + cos 𝜃
−1
or C = 449 N
32.3° ▹
𝑷 𝐬𝐢𝐧 𝜽
𝑪 =
(𝑉)
𝟏 + 𝐜𝐨𝐬 𝜽
𝐶𝑜𝑚𝑜 𝜃 = 60° 𝑠𝑒𝑔𝑢𝑛 𝑒𝑛𝑢𝑛𝑐𝑖𝑎𝑑𝑜
De (I) se tiene que:
𝑻=
𝑃
𝑃
𝑃
𝟐
=
=
=
1
1 + cos 𝜃
1 + cos 60
𝟑
1 + 2
Vector Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
Elliot R. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell
© 2007 The McGraw-Hill Companies.
𝑷

5. Ahora De (V) se tiene que:
𝑪 =
𝑃 sin 𝜃
𝑃 sin 60
𝑃 0,87
=
=
= 𝟎, 𝟓𝟖 𝑷
1
1 + cos 𝜃
1 + cos 60
1 + 2