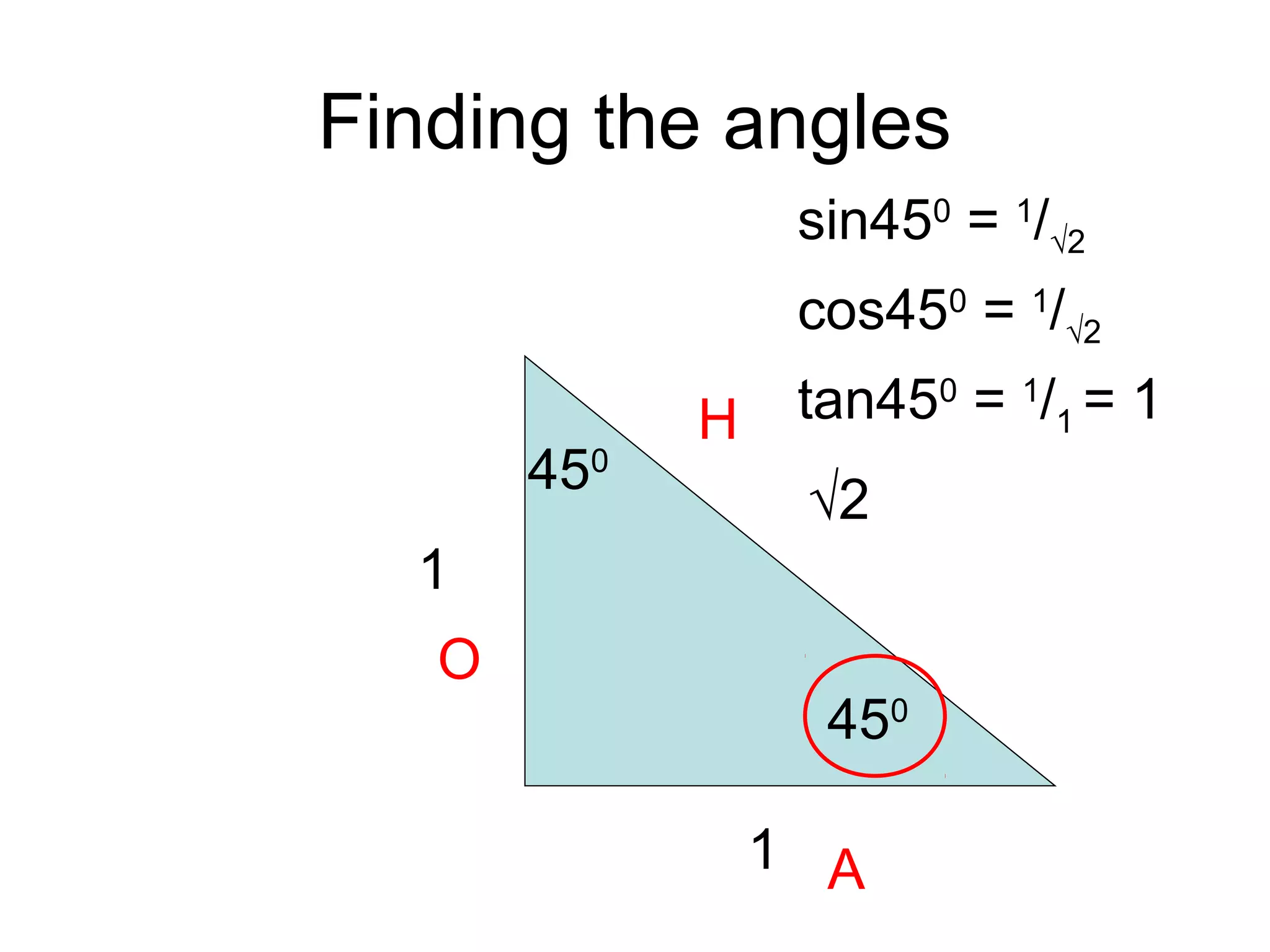
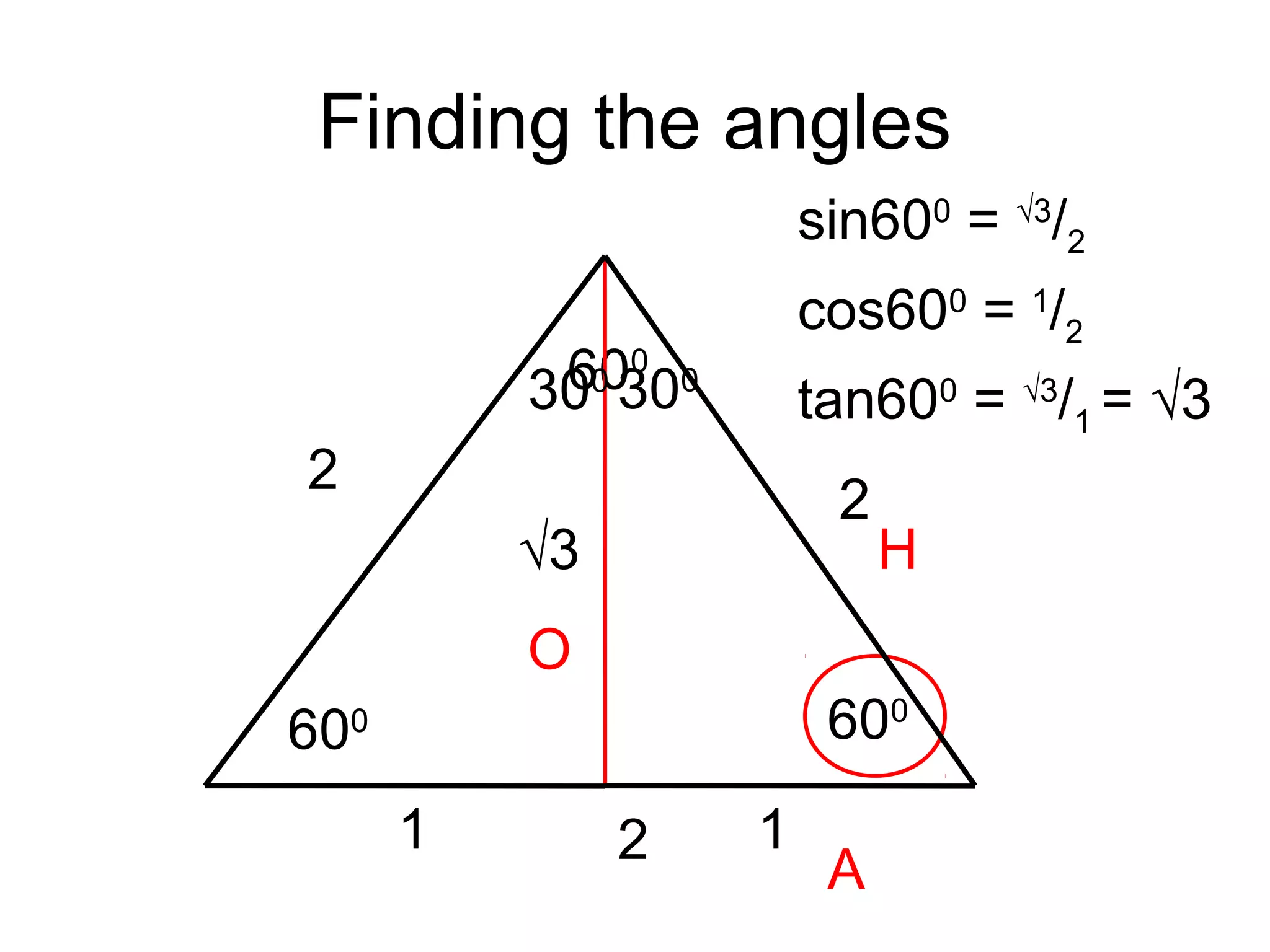
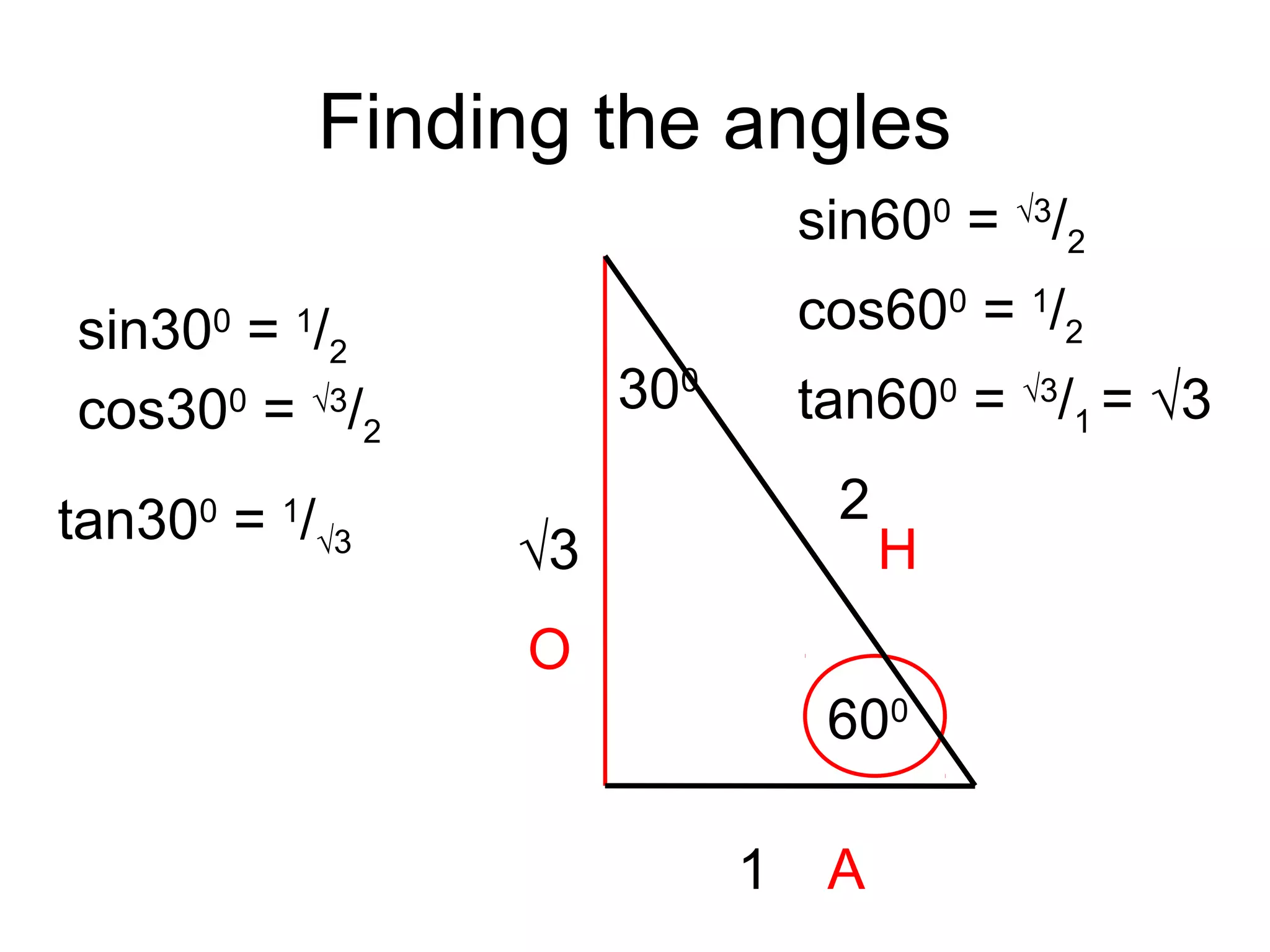
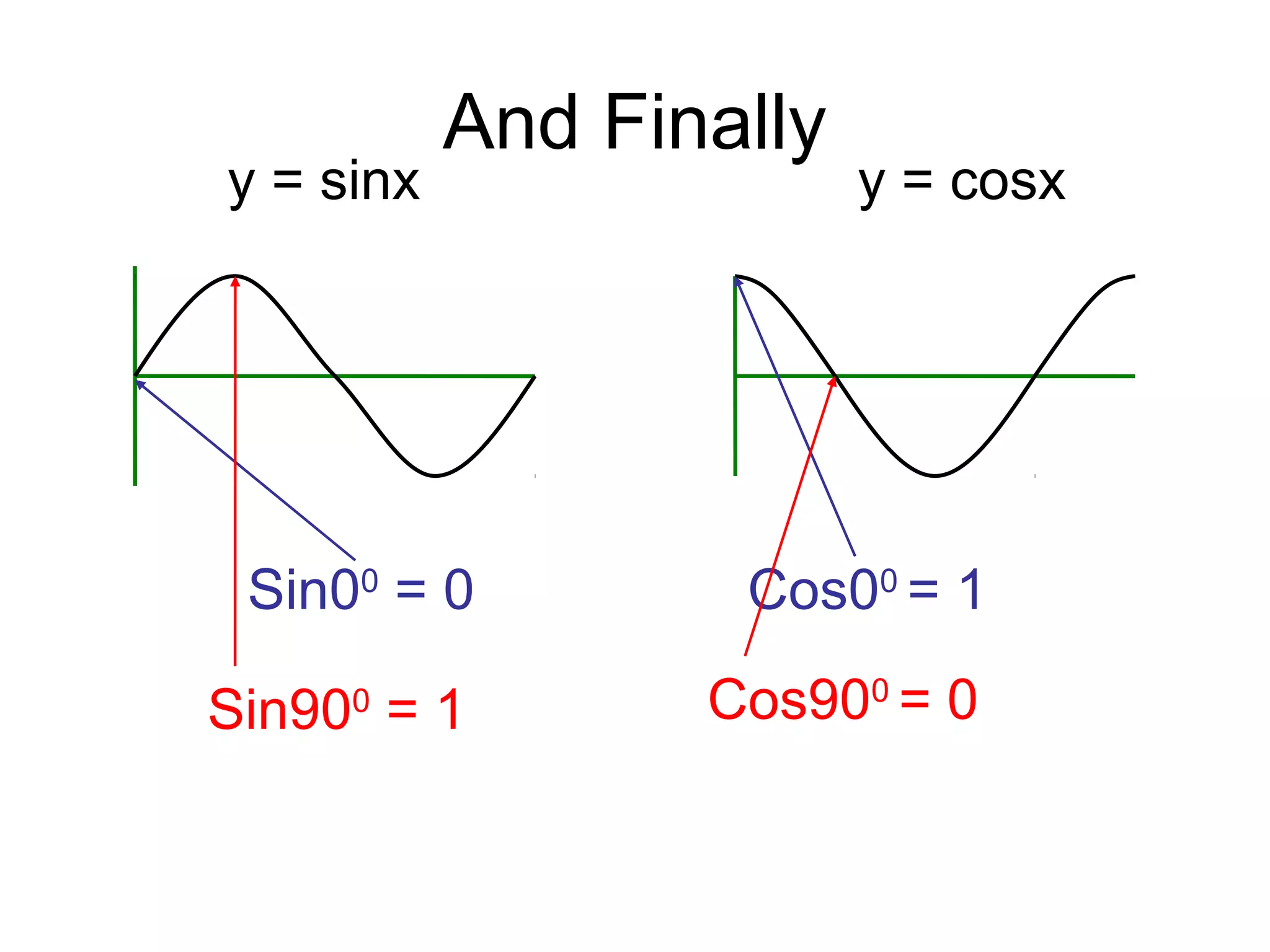
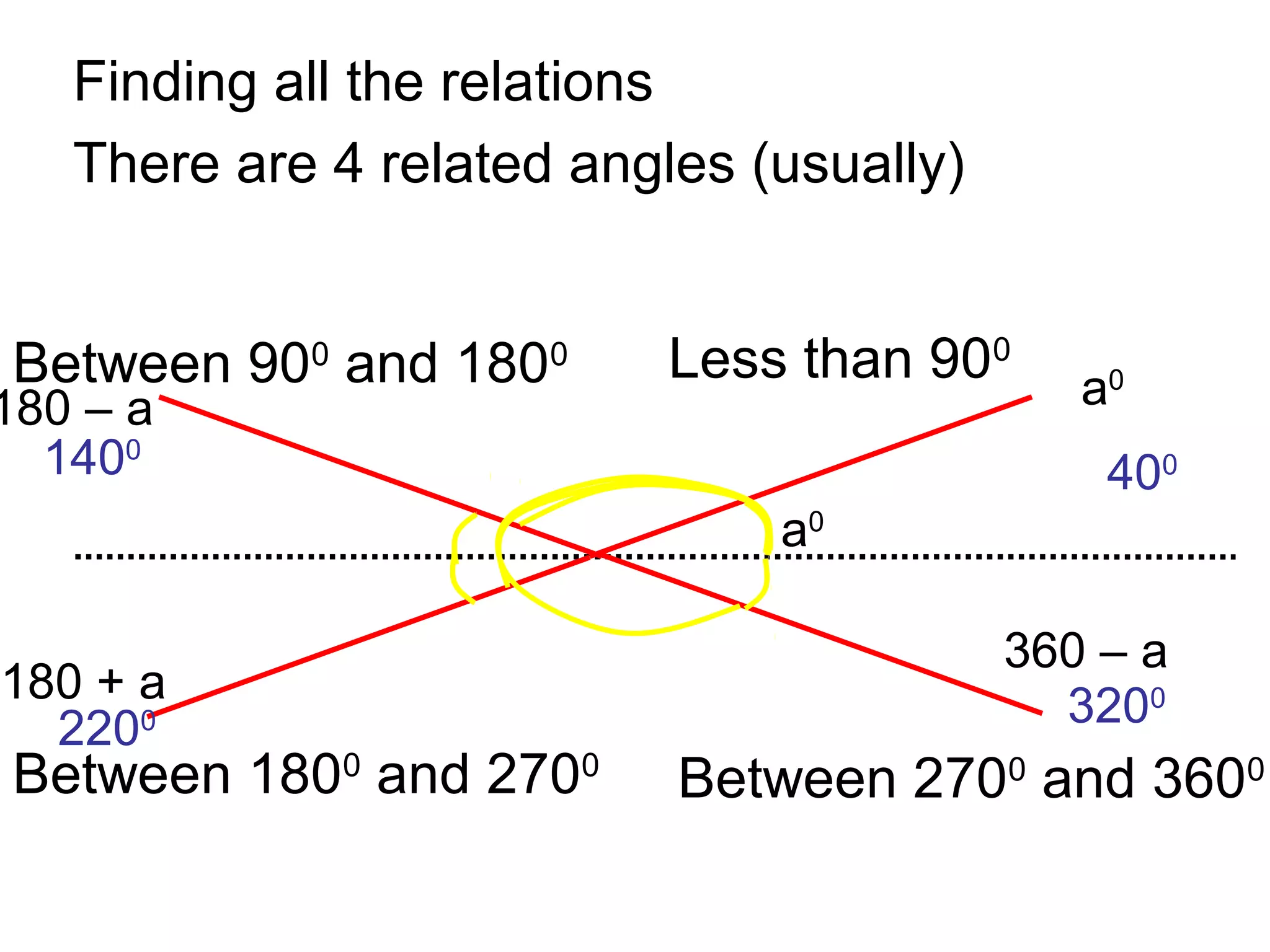
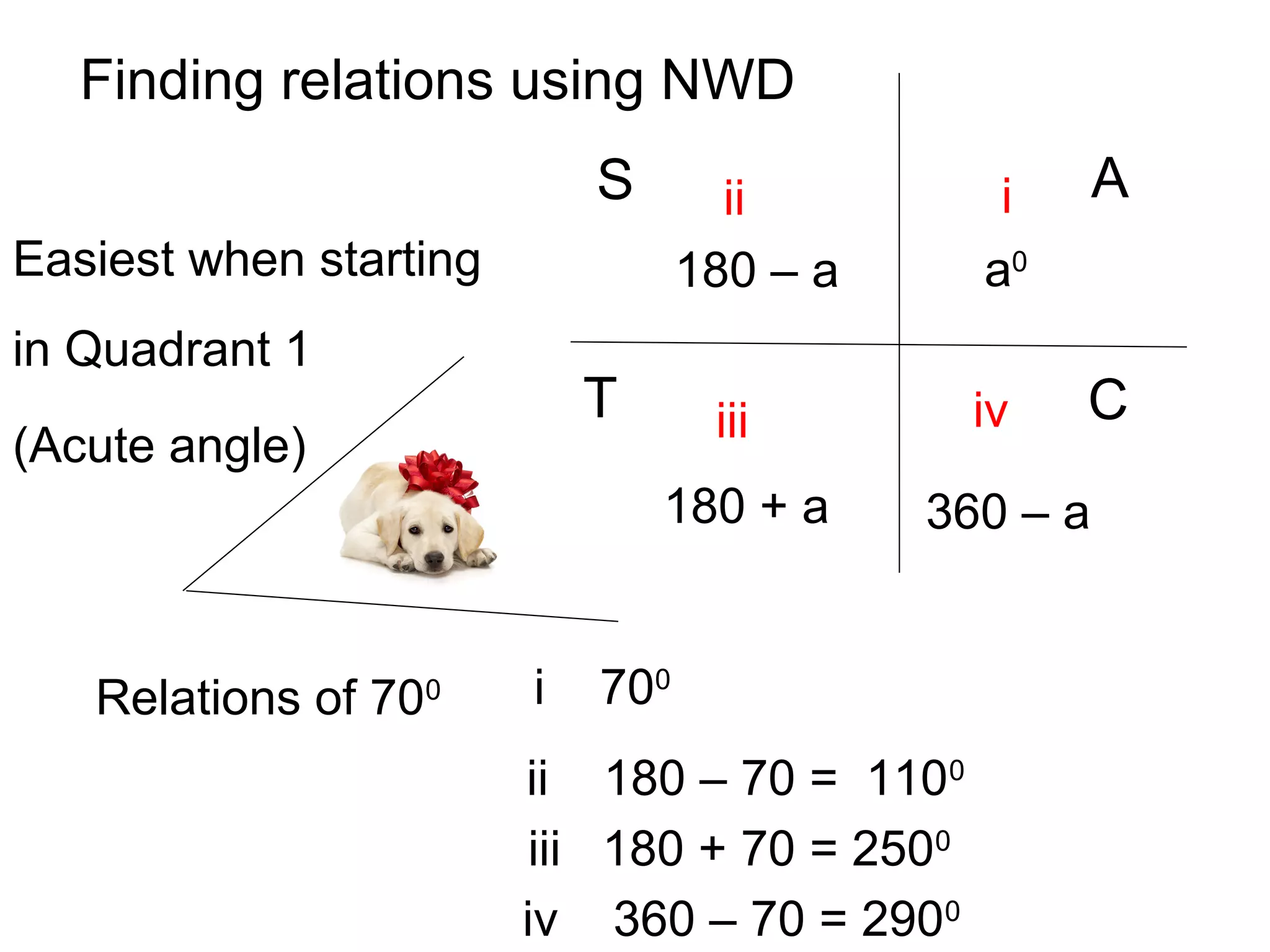
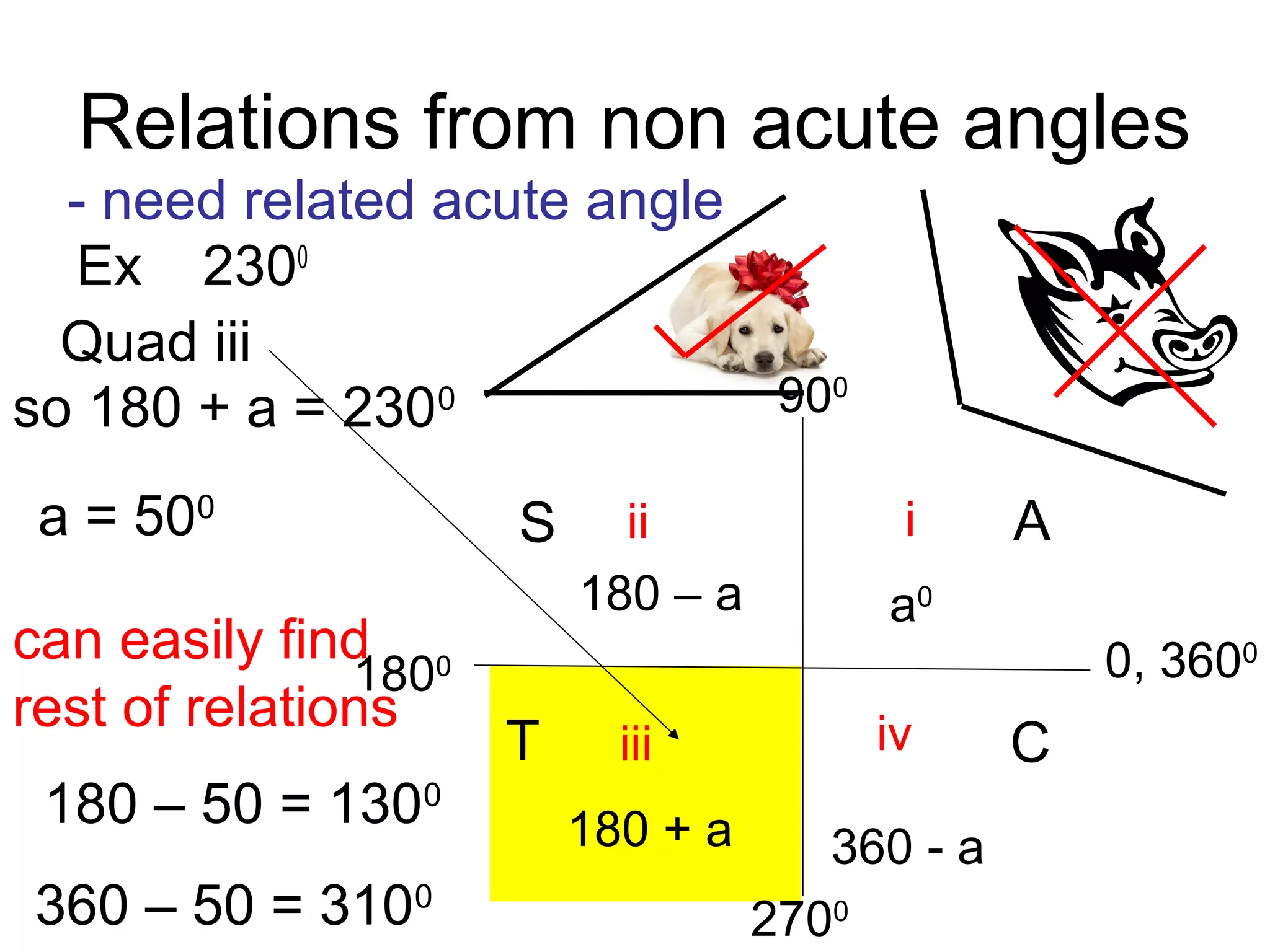
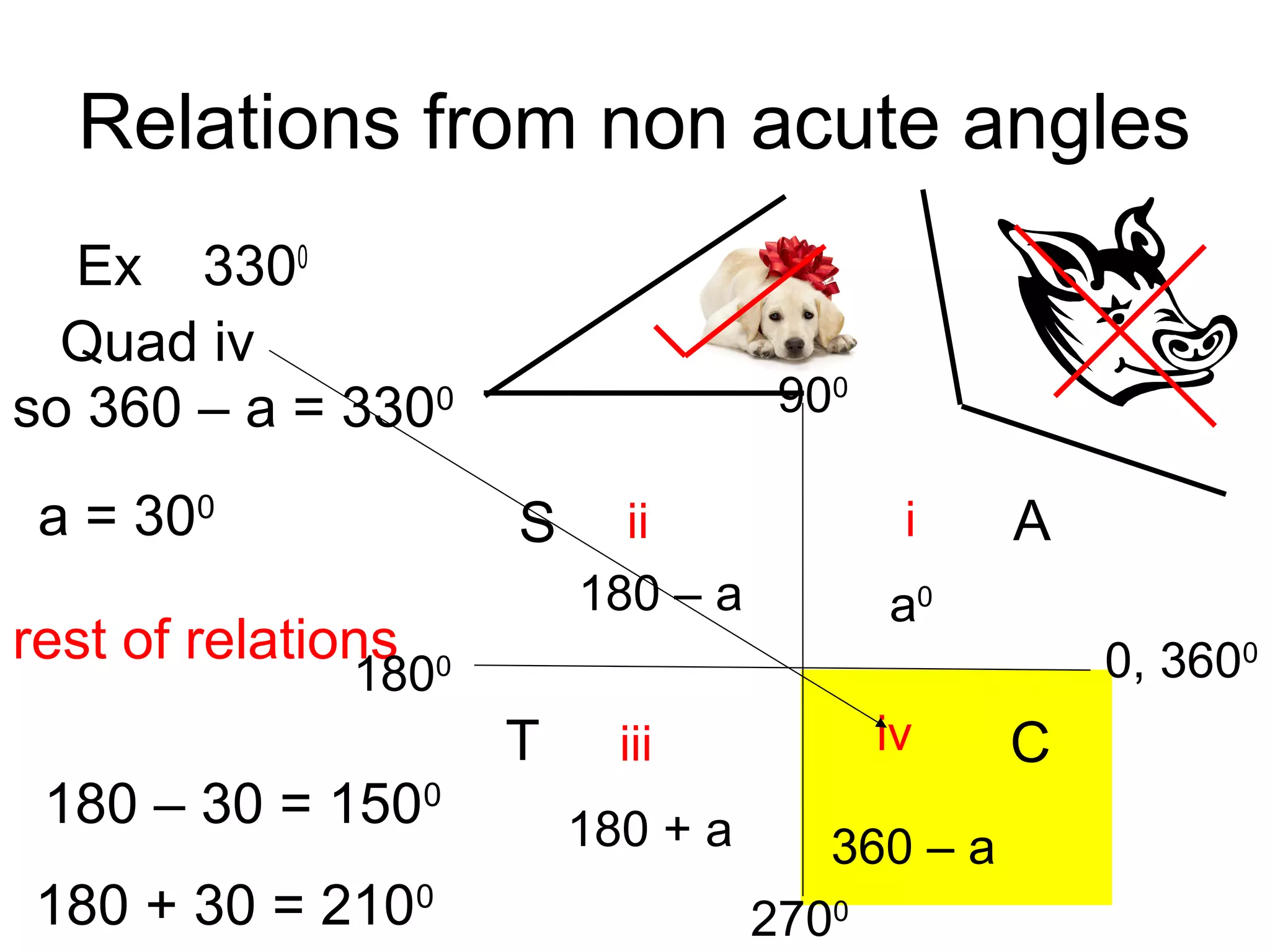
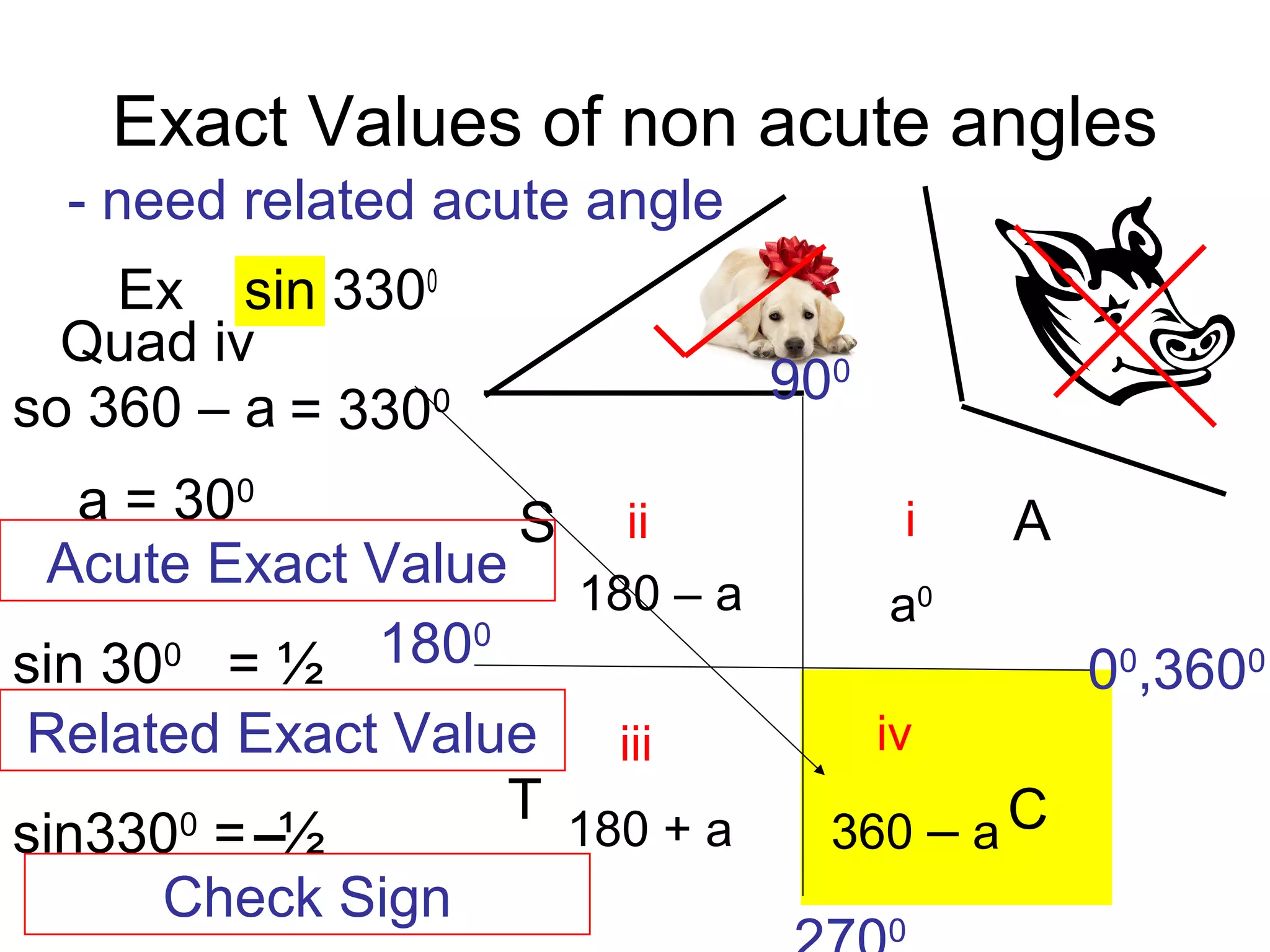
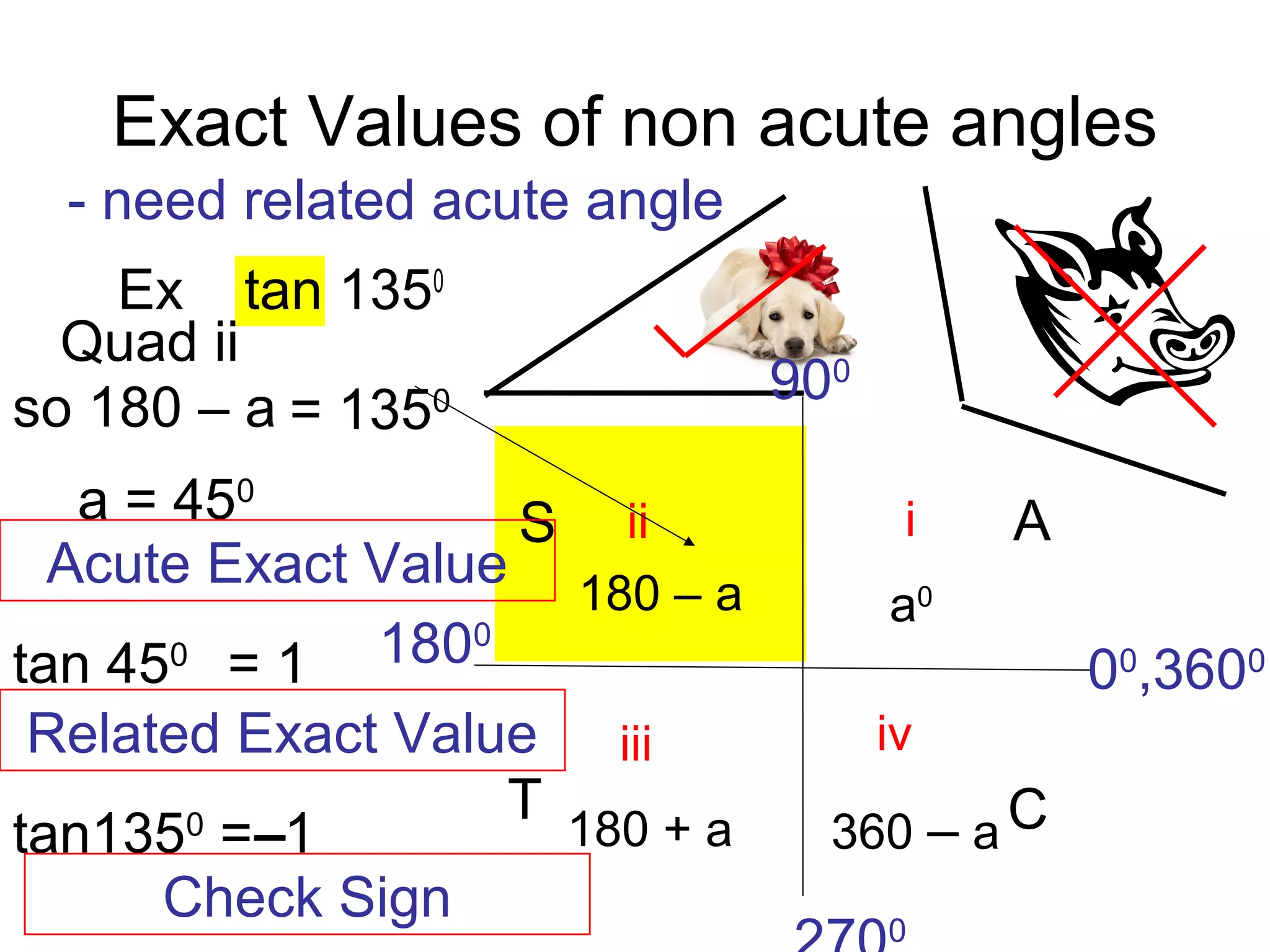
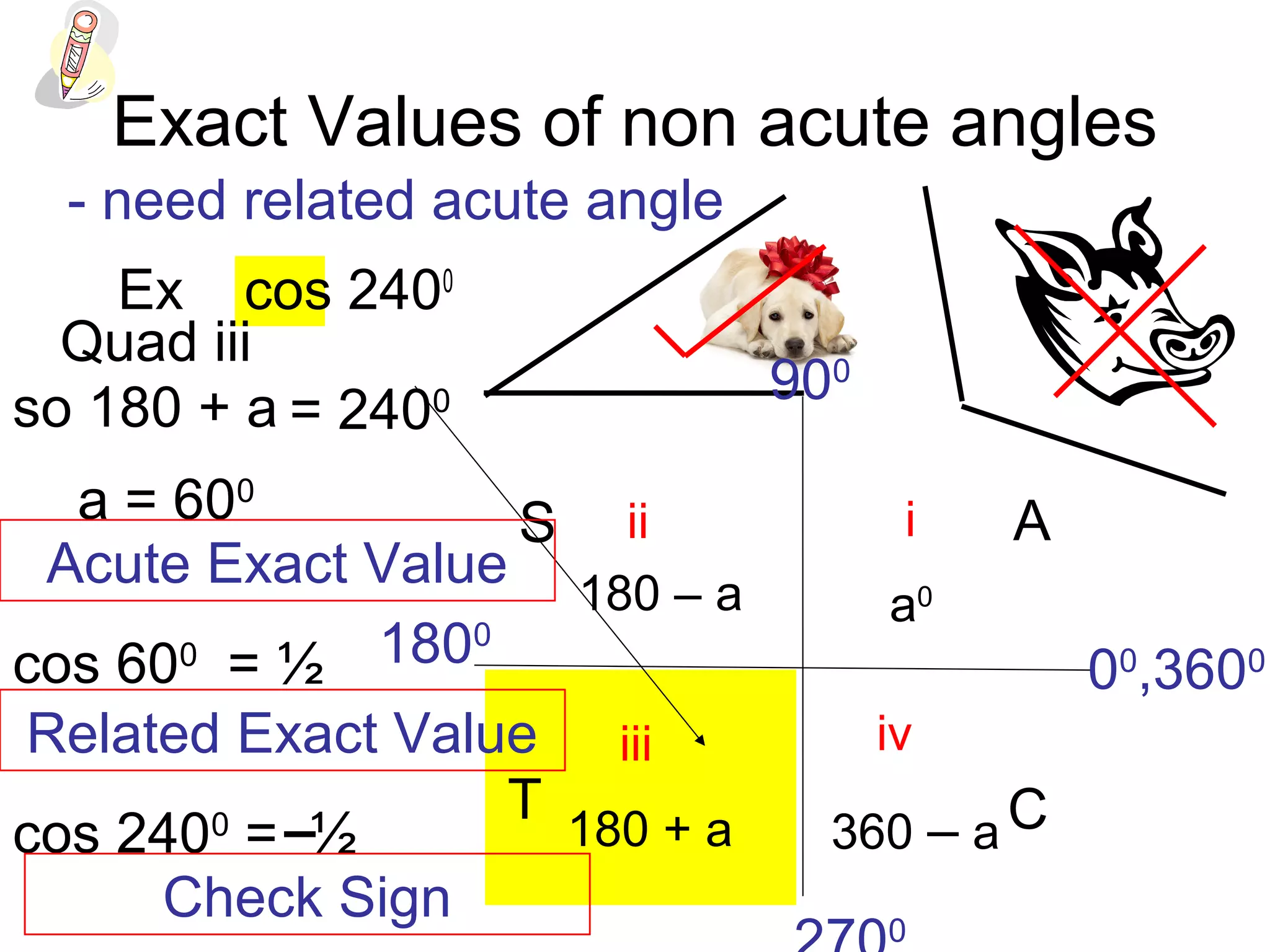
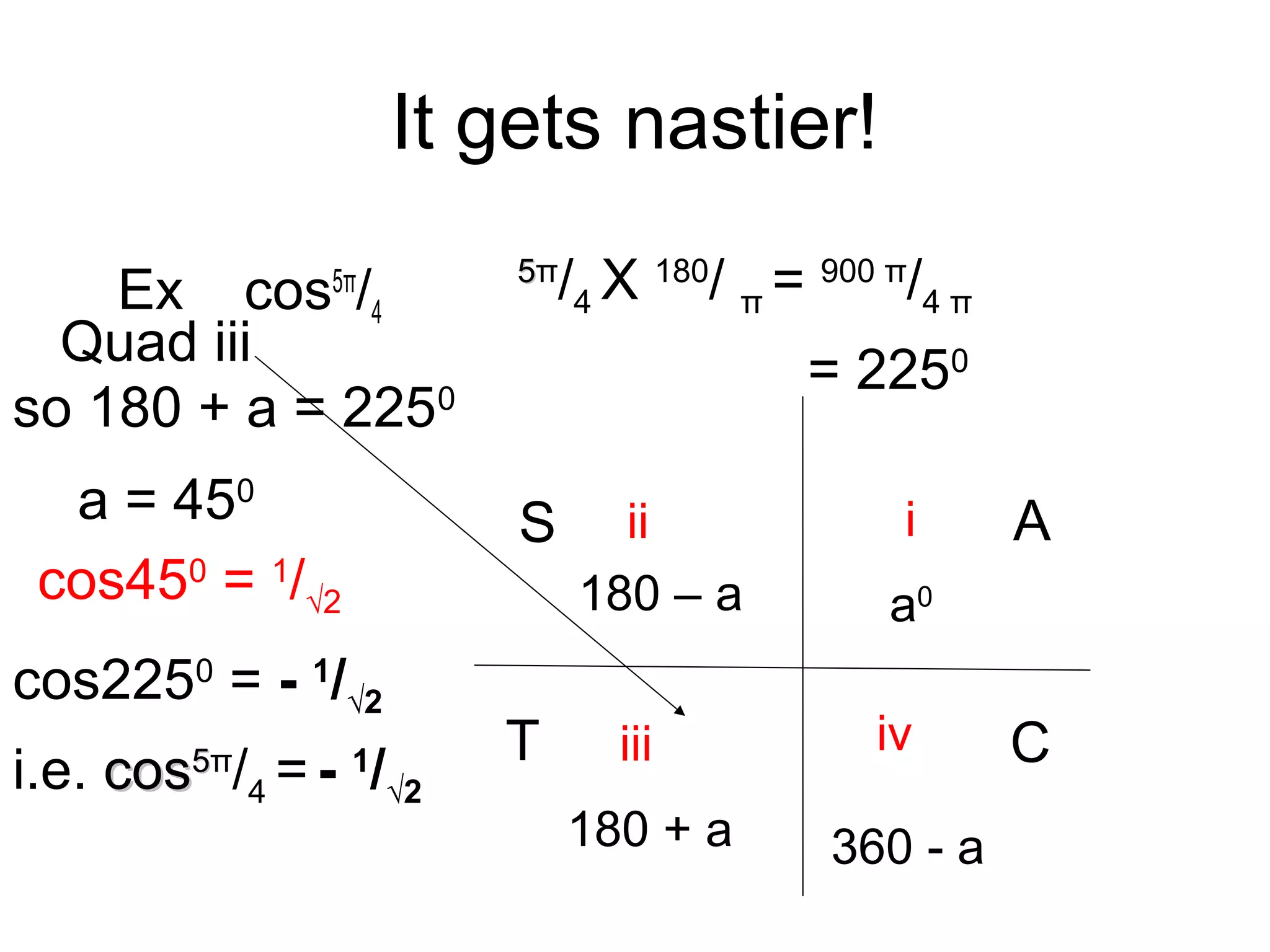
The document discusses exact trigonometric values of common angles such as 45°, 60°, 90° degrees. It provides the exact sine, cosine, and tangent values of these angles using definitions and right triangle relationships. The document also discusses finding the exact trig values of related angles that are not in the standard reference angles by using the relationships between complementary, supplementary, and coterminal angles.

1. Block 3
Exact Angles

2. What is to be Learned?
• The exact trig values of vital angles
• How to use exact values with related
angles

3. Finding the angles
450
450
1
1
√2
H
O
A
sin450
= 1
/√2
cos450
= 1
/√2
tan450
= 1
/1 = 1

4. Finding the angles
600
600
2
2
2
H
O
A
sin600
= √3
/2
cos600
= 1
/2
tan600
= √3
/1 = √3
600
1 1
300
300
√3

5. Finding the angles
600
2
H
O
A
sin600
= √3
/2
cos600
= 1
/2
tan600
= √3
/1 = √3
1
300
√3
cos300
= √3
/2
sin300
= 1
/2
tan300
= 1
/√3

6. And Finally
y = sinx y = cosx
Sin00
= 0
Sin900
= 1
Cos00
= 1
Cos900
= 0

7. Exact Values
There are some trig values we must
memorise – they are exact (not
approximations)

8. 0000
303000
454500
606000
909000
sin
cos
tan
0 π
/2
π
/3
π
/4
π
/6
degrees
rads
0 1½ 1
/√2
√3
/2
1 √3
/2
1
/√2 ½ 0
0 1
/√3 1 √3 ∞

9. Finding all the relations
There are 4 related angles (usually)
Less than 900
Between 900
and 1800
Between 1800
and 2700
Between 2700
and 3600
a0
a0
180 – a
180 + a
360 – a
3200
1400
2200
400

10. Finding relations using NWD
a0
180 – a
180 + a 360 – a
iii
iii iv
Easiest when starting
in Quadrant 1
(Acute angle)
Relations of 700 i 700
ii 180 – 70 = 1100
iii 180 + 70 = 2500
iv 360 – 70 = 2900
AS
T C

11. Relations from non acute angles
Ex 2300
180 – a
180 + a
iii
iii iv
a0
360 - a
AS
T C
Quad iii
so 180 + a = 2300
a = 500
can easily find
rest of relations
180 – 50 = 1300
360 – 50 = 3100
0, 3600
1800
2700
- need related acute angle
900

12. Relations from non acute angles
Ex 3300
180 – a
180 + a
iii
iii iv
a0
360 – a
AS
T C
Quad iv
so 360 – a = 3300
a = 300
rest of relations
180 – 30 = 1500
180 + 30 = 2100
0, 3600
900
1800
2700
900

13. Find relations of these angles
1. 1000
800
2600
2800
2. 2000
200
1600
3400
3. 3000
600
1200
2400
4. 1950
150
1650
3450
5. 3080
520
1280
2320

14. Exact Values of non acute angles
Ex sin 3300
180 – a
180 + a
iii
iii iv
a0
360 – a
AS
T C
Quad iv
so 360 – a
a = 300
sin 300
sin3300
= ½
- need related acute angle
–
= 3300 900
1800
0
Acute Exact Value
= ½
Related Exact Value
Check Sign
00
,3600

15. Exact Values of non acute angles
Ex tan 1350
180 – a
180 + a
iii
iii iv
a0
360 – a
AS
T C
Quad ii
so 180 – a
a = 450
tan 450
tan1350
= 1
- need related acute angle
–
= 1350 900
1800
0
Acute Exact Value
= 1
Related Exact Value
Check Sign
00
,3600

16. Exact Values of non acute angles
Ex cos 2400
180 – a
180 + a
iii
iii iv
a0
360 – a
AS
T C
Quad iii
so 180 + a
a = 600
cos 600
cos 2400
= ½
- need related acute angle
–
= 2400 900
1800
0
00
,3600
Acute Exact Value
= ½
Related Exact Value
Check Sign

17. You Try
1. sin1200
2. cos2400
3. tan1350
4. sin2250
5. tan2100
6. cos3300
7. sin1800
(beware!)
√3
/2
- ½
-1
- 1
/√2
1
/√3
√3
/2
0
Key Question

18. It gets nastier!
Ex cos5π
/4
180 – a
180 + a
iii
iii iv
a0
360 - a
AS
T C
Quad iii
so 180 + a = 2250
a = 450
cos450
= 1
/√2
cos2250
= - 1
/√2
55π
/4 X 180
/ π = 900 π
/4 π
= 2250
i.e. coscos55π
/4 = - 1
/√2