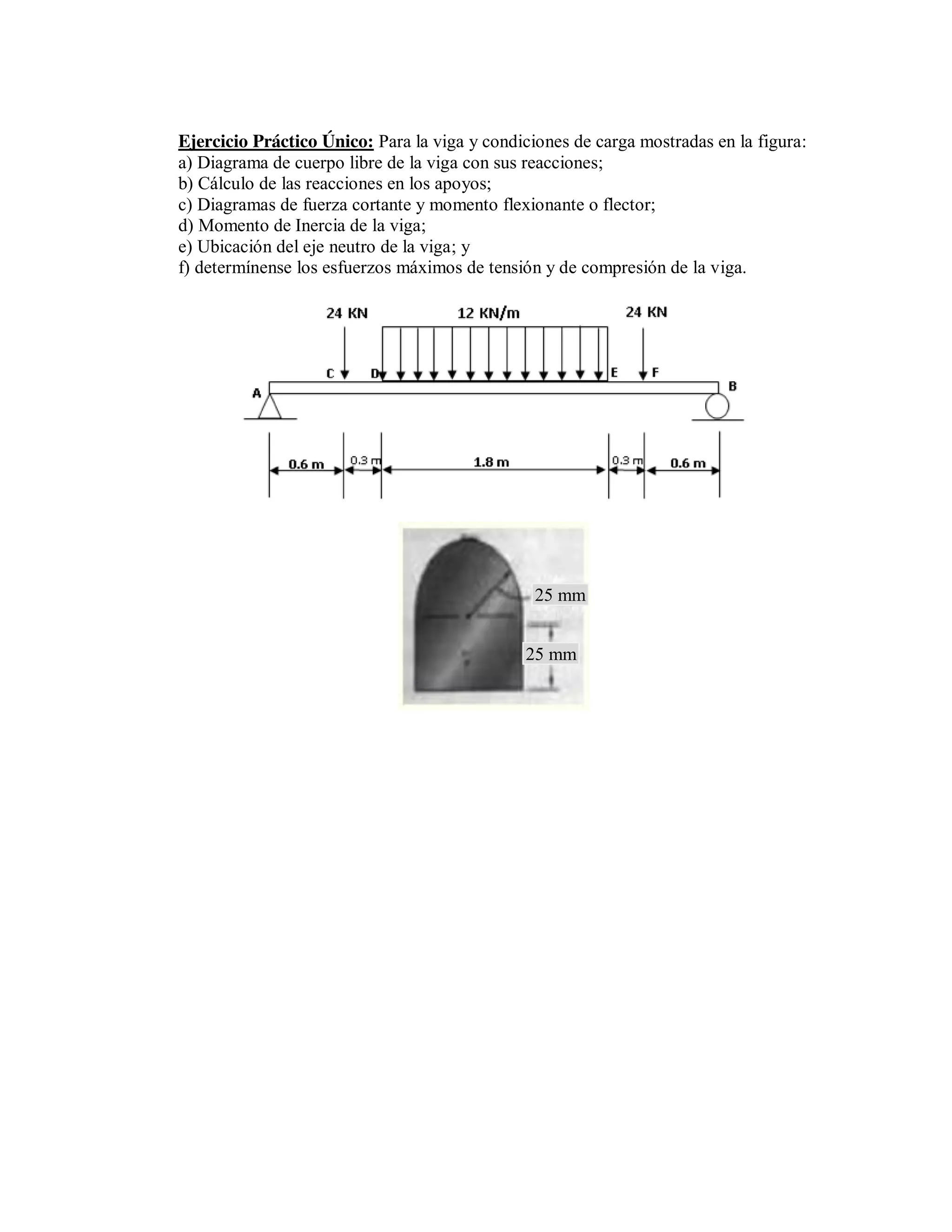
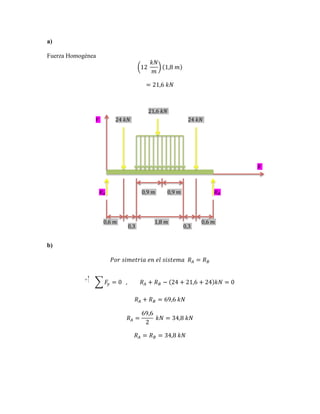
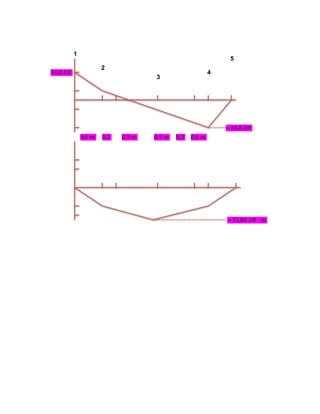
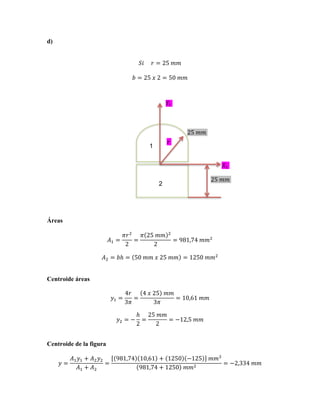
The document provides instructions to analyze a beam with given dimensions and loading conditions shown in a figure. It lists the following tasks: 1) Create a free body diagram of the beam and determine reactions. 2) Calculate shear and bending moment diagrams. 3) Determine the beam's moment of inertia and neutral axis. 4) Find the maximum stresses - tension and compression - in the beam.

1. Ejercicio Práctico Único: Para la viga y condiciones de carga mostradas en la figura:
a) Diagrama de cuerpo libre de la viga con sus reacciones;
b) Cálculo de las reacciones en los apoyos;
c) Diagramas de fuerza cortante y momento flexionante o flector;
d) Momento de Inercia de la viga;
e) Ubicación del eje neutro de la viga; y
f) determínense los esfuerzos máximos de tensión y de compresión de la viga.
25 mm
25 mm

2. Free-Body Diagram:
Chapter 4, Solution 19.
b)
and
0,6!!!
𝑃𝑜𝑟 𝑠𝑖𝑚𝑒𝑡𝑟𝑖𝑎 𝑒𝑛 𝑒𝑙 𝑠𝑖𝑠𝑡𝑒𝑚𝑎 𝑅! = 𝑅!
𝐹! = 0 ,
𝑅! =
( 380 )2 + ( 240 )2
= 449.44 N
C y = 240 N
32.3° ▹
Fuerza Homogénea
12
𝑘𝑁
𝑚
0,9!!!
or C = 449 N
⎛ Cy ⎞
− 240 ⎞
⎟ = tan −1 ⎛
⎟ = 32.276°
⎜
⎟
⎝ − 380 ⎠
⎝ Cx ⎠
2
2
Cx + C y =
0,3!
θ = tan −1 ⎜
⎜
C =
or
!!
∴ C y = −240 N
C x = 380 N
∴ TAB = 300
!!
Then
or
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
∴ C x = −380 N
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
(b) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
(a) From free-body diagram of lever BCD
COSMOS: Complete Online Solutions Manual Organization System
a)
1,8 𝑚
= 21,6 𝑘𝑁
21,6!!"!
24!!"!
24!!"!
!!
0,9!!!
1,8!!!
!!
0,3!
𝑅! + 𝑅! = 69,6 𝑘𝑁
69,6
𝑘𝑁 = 34,8 𝑘𝑁
2
𝑅! = 𝑅! = 34,8 𝑘𝑁
0,6!!!
𝑅! + 𝑅! − 24 + 21,6 + 24 𝑘𝑁 = 0

3. (b) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) TAB
∴ −2
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
ΣFx = 0: 200(b) +From free-body diagram of lever BCD
N Cx + 0.6 ( 300 N ) = 0
∴ C x = −380 N
or
C x = 380 N
∴ C x = −380 N
or
C = 380 NC + 0.6 ( 300 N ) = 0
ΣFx = 0: x 200(b) +From free-body diagram of lever BC
N
x
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
(a) From free-body diagram of lever BCD
ΣFy = 0: C y + 0.8 ( 300 N ) = 0 ∴ C = −380 N
ΣFx = 0: x 200 N + Cx + 0.
or
C = 380 N
x
∴ C y = −240 N
or
C y = 240 N
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
∴ C y = −240 N
or y = 0: y C y + 0.8 ( 300 N ) = 0 ∴ C x = −380 N
C = 240 N
ΣF
2
2
2
2
C = C x + C y = ∴(TAB )= + ( 240 ) = 449.44 N
380 300
Then
2
2
ΣF
2
2
or y = 0: y C y + 0.8 ( 300 N
C = 240 N
C = C x + C y = ( 380 ) + ( 240 ) ∴ C y = −240 N
= 449.44 N
Then
(b) From free-body diagram of lever BCD
Cy ⎞
⎛
⎛ − 240 ⎞
2
2 ∴ C y = −240 N
and
θ = tan −1 ⎜ ⎟ = tan −1 ⎜
2
⎟ = 32.276°
C
Cx + 2
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = ⎜ C x ⎟
0 ⎠
⎝ − 380 ⎠= tan −1 ⎛ C y ⎞ Then −1 ⎛ − 240 ⎞ = 32.276°C y = ( 380 ) + ( 240 ) = 449.44 N
⎝
⎟
⎜
and
θ
⎜ C ⎟ = tan ⎜ − 380 ⎟ =
2
2
2
⎠
C
⎠
⎝
∴ C x = −380 N
or
C x = 380 N
or C =x 449 N ⎝32.3° ▹
⎛ C y ⎞ Then −1 ⎛ − 240 ⎞ = C x + C y = ( 380 )
−1
⎟
⎜
and
θ = tan C = 449 tan ⎜32.3° ▹= 32.276°
or ⎜ C ⎟ = N ⎝ − 380 ⎟
⎠
⎝ x⎠
⎛ Cy ⎞
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
⎛ − 24
and
θ = tan −1 ⎜ ⎟ = tan −1 ⎜
⎜ = ⎟
− 38
or C C x 449 N ⎝32.3
⎠
⎝
∴ C y = −240 N
or
C y = 240 N
Free-Body Diagram:
(a) From free-body diagram of lever BCD
Chapter 4, Solution 19.
(a) From 200
ΣM C = Free-Body Diagram: N ( 75 mm ) = of lever BCD
0: TAB ( 50 mm ) −free-body diagram 0
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
(a) From AB
∴ T free-body
Free-Body Diagram:= 300 diagram of lever BCD
∴ − 200 N ( 75
ΣM = 0: T ( 50 mm ) TAB = 300 diagram of lever BC
(b) From free-body diagram of lever BCD
(a) From free-body mm ) = 0
: Complete Online Solutions Manual Organization System
c) Se consideran 5 secciones en la viga:
COSMOS: Complete Online Solutions Manual Organization System
er 4, Solution 19.
AB
Body Diagram:
1.
𝐹! = 0 , 34,8 𝑘𝑁 − 𝑉! = 0 ⇒ 𝑉! = 34,8 𝑘𝑁
(a) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝑀! = 0 , 34,8 𝑘𝑁 0 𝑚 + 𝑀! = 0 ⇒ 𝑀! = 0
ion 19.
am:
C
ine Solutions Manual Organization System
(b) From free-body diagram of lever BCD
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
2.
∴ C = −380 N
C = 380 N
or
x
𝐹! = 0 , x 34,8 − 24 𝑘𝑁 − 𝑉! = 0 ⇒ 𝑉! = 10,8 𝑘𝑁
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
(a) From free-body diagram of lever BCD
∴C
−240 N
or
ΣM C = 0: TAB ( 50 mm ) y−=200 N ( 75 mm ) = 0 C y = 240 N
𝑀! = 0 , 34,8 0,6 𝑘𝑁 ∙ 𝑚 + 𝑀! = 0 ⇒ 𝑀! = −20,88 𝑘𝑁 ∙ 𝑚
C
AB
𝑀! = 0, 34,8 3 − 24 2,4 − 21,6 1,2 𝑘𝑁 ∙ 𝑚 + 𝑀! = 0
(
2
+ ( 240 ) =
)2−20,88 𝑘𝑁 449.44 N
∙ 𝑚
C = C x + C y = 380
Then
OSMOS: Complete Online Solutions Manual Organization System =
⇒ 𝑀!
2
2
∴ TAB = 300
, Solution 19.
and
C =
θ = tan −1 ⎜
⎜
Then
and
ΣM C =2 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
( 380𝑀! + (0 , 𝑃𝑜𝑟 𝑠𝑖𝑚𝑒𝑡𝑟𝑖𝑎 ⇒ 𝑀! = 0
) = 240 )2 = 449.44 N
∴ TAB = 300
⎛ Cy ⎞
⎛ − 240 ⎞
−1
⎟ free-body diagram.276°
⎜
θ = tan(b) From tan −1 ⎜
⎟ = 32 of lever BCD
⎜C ⎟=
⎝ − 380 ⎠
⎝ x⎠
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
or C = 449 N
32.3° ▹
∴ C x = −380 N
or
C x = 380 N
C =
Then
2
2
Cx + C y =
y Diagram:
mplete Online Solutions Manual Organization System
(b) From free-body diagram of lever BCD
⎛ Cy ⎞
1 ⎛ − 240 ⎞
and
θ = tan −1 ⎜0: ⎟ = tan −+⎜Cx + 0.6= 300276°= 0
ΣFx = ⎜
200
⎟ N ⎝ − 380 ⎟ ( 32. N )
⎠
⎝ Cx ⎠
hapter 4, Solution 19.5.
∴ C x = −380 N
or
C = 380 N
or C = x449 N
32.3° ▹
ΣFy = 0: C y + 0.8 ( 300 N ) = 0 𝐹 = 0 ⇒ 𝑉! = 0
!
Free-Body Diagram:
(a) C y = −free-body diagram C ylever BCD
of = 240 N
∴ From 240 N
or
Free-Body Diagram:
or C = 449 N
2
2
2
2
∴T
C = C x + C y = ( 380 ) + ( 240 ) = 449.44 N AB = 300
Then
(b) From free-body diagram of lever BCD
⎛ Cy ⎞
⎛ − 240 ⎞
−1
⎜
and 4.ΣFx θ = tan200 N ⎟ = tan −10.6 ( 300⎟N )32.276°
= 0:
+
⎜ C ⎟ Cx + ⎜ − 380 ⎠ = = 0
⎝
⎝ x⎠
∴ C x = −380 N
or
C x = 380 N
or − 449 N
𝐹! = 0 , 34,8 − 24 − 21,6C =24 𝑘𝑁 −32.3=▹ ⇒ 𝑉! = −34,8 𝑘𝑁
𝑉! ° 0
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
(a) From free-body diagram of lever BCD
ΣM =∴ C yT= −240mm ) − or N ( C y mm ) =N
0:
200 75 = 240 0
( 50 N
⎛ Cy ⎞
− 240 ⎞
⎟ = tan −1 ⎛
⎟ = 32.276°
⎜
⎟
⎝ − 380 ⎠
⎝ Cx ⎠
m:
𝑀! = 0, 34,8 1,8 − 24 1,2 𝑘𝑁 ∙ 𝑚 + 𝑀! = 0 ⇒ 𝑀! = −33,84 𝑘𝑁 ∙ 𝑚
( 380 )2 + ( 240 )2
Chapter 4, Solution 19.
n 19.
AB
= 449.44 N
C
Solutions Manual Organization System
32.3° ▹
2
2 ∴ T
2
2
AB = 300
C = C x + C y = ( 380 ) + ( 240 ) = 449.44 N
Then
(b) From free-body diagram of lever BCD
⎛ Cy ⎞
⎛ − 240 ⎞
−1
= tan −1 ⎜
⎟
3. and Fx = 0: θ = tan + ⎜Cx +⎟ 0.6 ( 300 N ) = 0 = 32.276°
Σ
200 N ⎜
Cx ⎟
⎝ − 380 ⎠
⎠
⎝
∴ C x = −380 N
or
C x = 380 N
or
= 449 N
32.3 ▹
𝐹! = 0 , 34,8 − 24 − 21,6 𝑘𝑁 −C 𝑉! = 0 ⇒ 𝑉!°= −10,8 𝑘𝑁
ΣFy = 0: C + 0.8 ( 300 N ) = 0
(a) From free-body diagram ofy lever BCD
ΣM = 0: T ∴ (C y mm240 N N ( 75 mmC = = 240 N
50 = − ) − 200 or
)y 0
2
2
Cx + C y =
Chapter 4, Solution 19.
olutions Manual Organization System
19.
∴ TAB = 300
( 300 N ) = 0
chanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr.,
senberg, William E. Clausen, David Mazurek, Phillip J. Cornwell ΣFy = 0: C y + 0.8
he McGraw-Hill Companies.

4. 1
34,8!!"!
5
2
3
4
−34,8!!"!
0,6!!! 0,3!
0,9!!!
0,9!!! 0,3! 0,6!!!
−33,84!!" ∙ !!

5. d)
𝑆𝑖 𝑟 = 25 𝑚𝑚
𝑏 = 25 𝑥 2 = 50 𝑚𝑚
!! !
25!!!!
!!
1
!! !
25!!!!
2
Áreas
𝐴! =
𝜋𝑟 !
𝜋 25 𝑚𝑚
=
2
2
!
= 981,74 𝑚𝑚!
𝐴! = 𝑏ℎ = 50 𝑚𝑚 𝑥 25 𝑚𝑚 = 1250 𝑚𝑚!
Centroide áreas
𝑦! =
4𝑟
4 𝑥 25 𝑚𝑚
=
= 10,61 𝑚𝑚
3𝜋
3𝜋
𝑦! = −
ℎ 25 𝑚𝑚
=
= −12,5 𝑚𝑚
2
2
Centroide de la figura
𝑦=
𝐴! 𝑦! + 𝐴! 𝑦!
=
𝐴! + 𝐴!
981,74 10,61 + 1250 −125 𝑚𝑚!
= −2,334 𝑚𝑚
981,74 + 1250 𝑚𝑚!

6. Esto responde la pregunta e) ubicación del eje neutro que se encuentra en el
centroide de la figura.
𝐼! = 𝐼𝑥! − 𝐴! 𝑦! ! =
𝜋𝑟 !
𝜋 25 𝑚𝑚
− 𝐴! 𝑦! ! =
8
8
!
− 981,74 𝑚𝑚! 10,61 𝑚𝑚
!
𝐼! = 42881,54 𝑚𝑚!
𝑑! = 𝑦! − 𝑦 = 10,61 𝑚𝑚 + 2,334 𝑚𝑚 = 12,944 𝑚𝑚
𝑰 𝟏 = 𝐼! + 𝐴! 𝑑! ! = 42881,54 𝑚𝑚! + 981,74 𝑚𝑚! 12,944
𝐼! =
𝑏ℎ!
50 𝑚𝑚 25 𝑚𝑚
=
12
12
!
!
= 207369,26 𝑚𝑚!
= 65104,16 𝑚𝑚!
𝑑! = 𝑦! − 𝑦 = −12,5 𝑚𝑚 + 2,334 𝑚𝑚 = 10,166 𝑚𝑚
𝑰 𝟐 = 𝐼! + 𝐴! 𝑑! ! = 65104,16 𝑚𝑚! + 1250 𝑚𝑚! 10,166
!
= 194288,6 𝑚𝑚!
El momento de Inercia d) es
𝐼 = 𝑰 𝟏 + 𝑰 𝟐 = 207369,26 𝑚𝑚! + 194288,6 𝑚𝑚! = 401657,86 𝑚𝑚!
𝐼 = 401,65 𝑥 10!! 𝑚𝑚!
f) Esfuerzo máximo de tensión y compresión
𝑦! = 25 𝑚𝑚 + 2,334 𝑚𝑚 = 27,334 𝑚𝑚 = 0,027334 𝑚
𝑦! = −25 𝑚𝑚 + 2,334 𝑚𝑚 = −22,666 𝑚𝑚 = 0,022666 𝑚
𝜎! = −
𝜎! = −
𝑀𝑦!
−33,84 𝑘𝑁 ∙ 𝑚 0,027334 𝑚
=−
= 2,3 𝐺𝑃𝑎
𝐼
401,65 𝑥 10!! 𝑚!
𝑀𝑦!
−33,84 𝑘𝑁 ∙ 𝑚 −0,022666 𝑚
=−
= −1,9 𝐺𝑃𝑎
𝐼
401,65 𝑥 10!! 𝑚!