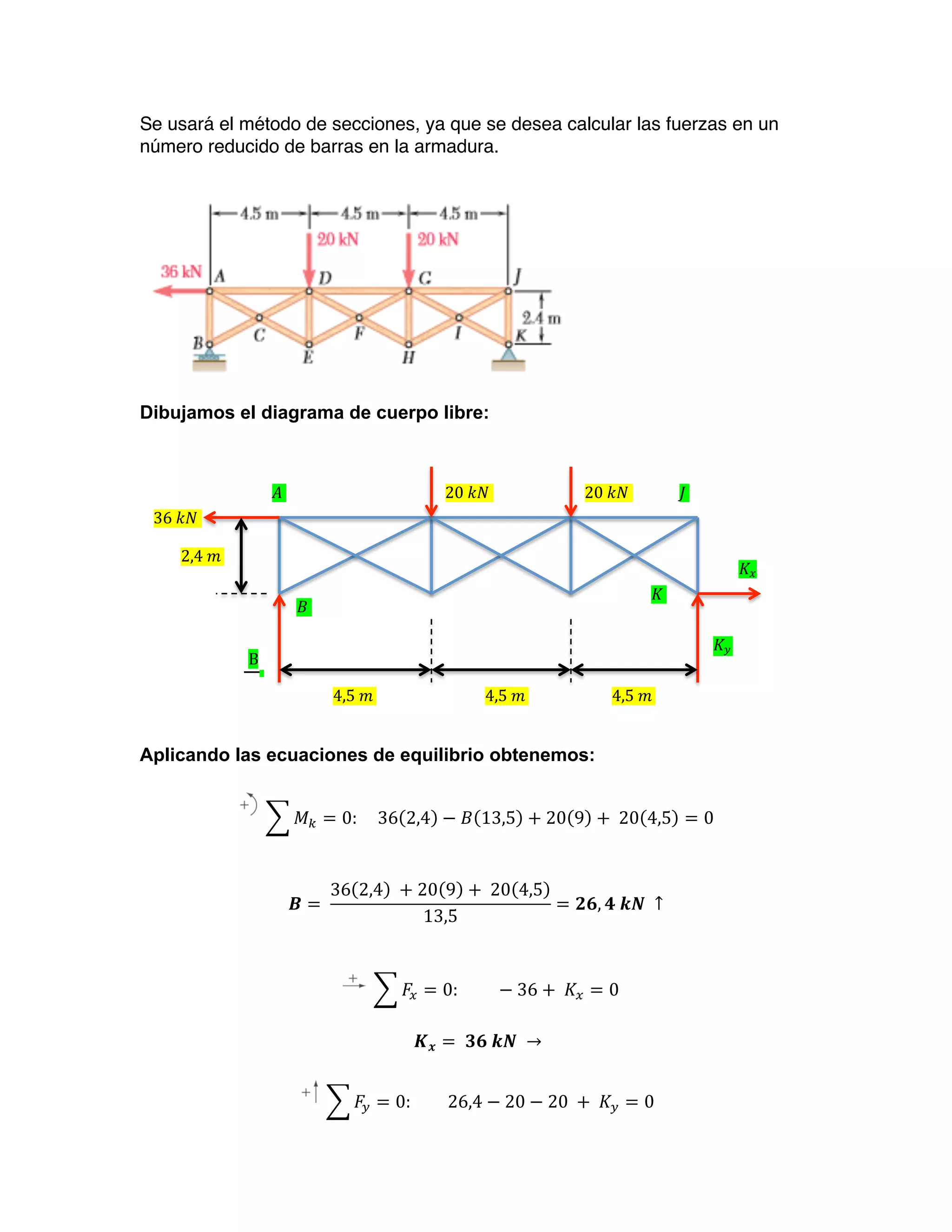
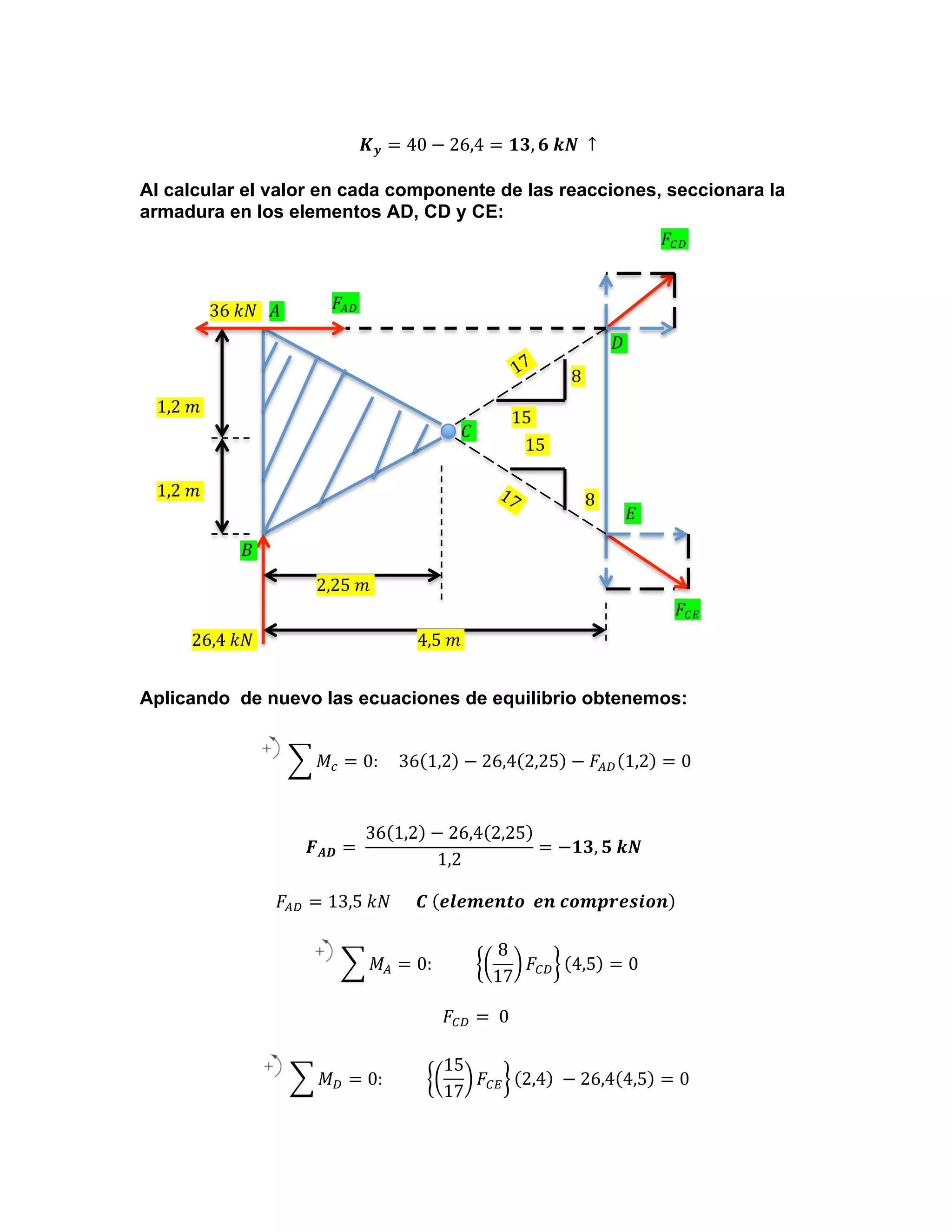
1) The method of sections will be used to calculate the forces in a reduced number of bars in the reinforcement. 2) Applying the equations of equilibrium to the free-body diagram yields the values of the reaction forces and internal forces. 3) The reinforcement will be sectioned in elements AD, CD and CE based on calculating the value of each component of the reactions.

1. Se usará el método de secciones, ya que se desea calcular las fuerzas en un
número reducido de barras en la armadura.
Dibujamos el diagrama de cuerpo libre:
!!
20!!"!
20!!"!
!!
36!!"!
2,4!!!
!!
!!
!!
omplete Online Solutions Manual Organization System
!!
B
!
4, Solution 19.
4,5!!!
4,5!!!
4,5!!!
COSMOS: Complete Online Solutions Manual Organization System
dy Diagram:
Aplicando las ecuaciones de equilibrio obtenemos:
OSMOS: Complete Online Solutions (a) From free-body diagram
Manual Organization System
Chapter 4, Solution 19.
of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝑀! = 0: 36 2,4 − 𝐵 13,5 + 20 9 + 20 4,5 = 0
hapter 4, Solution 19.
Free-Body Diagram:
(b) From free-body diagram of lever BCD of lever BCD
(a) From free-body diagram
Free-Body Diagram:
Then
and
∴ TAB = 300
36 2,4 + 0: + 9 ( 300mm4,5 200
ΣFx = 0: 200M C +=C20 TAB + 20 ) )= 0 N ( 75 mm ) = 0
0.6 50 N −
Σ N
x
𝑩 =
= 𝟐𝟔, 𝟒 𝒌𝑵 ↑
(a) From free-body diagram13,5 BCD
of lever
∴ C x = −380 N
or
C x = 380 N
∴ TAB = 300
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
Σ(b) =From C y + 0.8 ( 300 N ) = of lever BCD
Fy 0: free-body diagram 0
∴ TAB = 300
ΣFx = 0: 200 N C36 + 300 0
x
∴ C y = −240 N 0: +−C y+=0.6 (𝐾! =N ) = 0
240 N
𝐹! = or
(b) From free-body diagram of lever BCD
∴ C x = −380 N
or
C x = 380 N
2
2
2
2
C = CΣFx C y 0: 200 N)+ + x 240 ) ( 300 N ) = N
C ( + 0.6 = 449.44 0
x + = = ( 380
𝑲 C + 0.8 ( 300
ΣFy = 0:𝒙 = y 𝟑𝟔 𝒌𝑵 →N ) = 0
or
C x = 380 N
C y ⎞ ∴ C x−1= − 380 ⎞
⎛
⎛ −240 N
θ = tan −1 ⎜ ⎟ = tan ⎜∴ C y = =240276° or
C y = 240 N
⎟ − 32. N
Σ⎜ C x=⎟ 0: C y ⎝ − 380 ⎠ N ) = 0
F
+ 0.8 ( 300
⎝y ⎠
𝐹! = 0: 26,4 − 20 −2 20 + 𝐾! = 0
2
2
2
C =C C x −+ C yN= or or = 449240240= 449.44 N
( 380 ) +C( y N ) 32.3° ▹
C
∴ y = 240
=
N
Then
2
2
⎛ − 240 =
2
2 ⎛C ⎞
C x = tany−1 = y( 380tan+1 ( 240 ) ⎞ =449.44 N
θ + C ⎜ ⎟= ) − ⎜
⎟ 32.276°
⎜C ⎟
⎝ − 380 ⎠
⎝ x⎠
⎛ Cy ⎞
⎛ − 240 ⎞
θ = tan −1 ⎜ ⎟ = tan −1 ⎜
⎟ = 32.276° or C = 449 N
⎜C ⎟
− 380
Then and C =
and
32.3° ▹

2. 𝑲 𝒚 = 40 − 26,4 = 𝟏𝟑, 𝟔 𝒌𝑵 ↑
Al calcular el valor en cada componente de las reacciones, seccionara la
armadura en los elementos AD, CD y CE:
!!"
!!"
36!!"! !!
!!
!
17
1,2!!!
8!
15!
15!
!!
1,2!!!
17
!
8!
!!
!!
OS: Complete Online Solutions Manual Organization System
2,25!!!
!!"
26,4!!"!
ter 4, Solution 19.
-Body Diagram:
4,5!!!
Aplicando de nuevo las ecuaciones de equilibrio obtenemos:
(a) From free-body diagram of lever BCD
ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0
𝑀! =
COSMOS: Complete Online Solutions Manual Organization System
0: 36 1,2 − 26,4 2,25 − 𝐹!" 1,2 = 0
∴ TAB = 300
(b) From free-body diagram of lever BCD
ΣFx = 0: 36 1,2+ −x26,4 ( 300 N ) = 0
200 N C + 0.6 2,25
𝑭 𝑨𝑫 =
Chapter 4, Solution 19.
∴ C x = −3801,2
N
OS: Complete Online Solutions Manual Organization System F
Σ y
Free-Body Diagram:
𝐹!" =
ter 4, Solution 19.
-Body Diagram:
Then
= −𝟏𝟑, 𝟓 𝒌𝑵
or
C x = 380 N
= 0: C y + 0.8 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒐 𝒆𝒏 𝒄𝒐𝒎𝒑𝒓𝒆𝒔𝒊𝒐𝒏
13,5 𝑘𝑁 𝑪 ( 300 N ) = 0
(a) From free-body diagram of lever BCD
∴ C y = −240 N
or
C y = 240 N
ΣM C = 0: TAB ( 50 mm8 − 200 N ( 75 mm ) = 0
) 2
𝑀!2 = ( 380 )2
2
C = C x + C y = 0: + ( 240 ) 𝐹!" 449.44 N 0
= 4,5 =
17
∴ TAB = 300
⎛ Cy ⎞
(b) From free-body diagram− 240 ⎞ 0 BCD
⎛ of lever
and
θ = tan −1 ⎜ ⎟ = tan −1 ⎜𝐹!" = ⎟ = 32.276°
⎜C ⎟
⎝ +C
(a) From free-body diagram of leverN380 ⎠x + 0.6 ( 300 N ) = 0
⎠
⎝
ΣFx x = 0: 200 −BCD
N
32.3°
ΣM C = 0: TAB (∴ C 15 380 N ( 75C = ) = C = 380 N ▹
50 mm ) − 200 N or or 4490
−
mm
x =
x
𝑀! = 0:
𝐹!"
2,4 − 26,4 4,5 = 0
17
∴ TAB = 300
ΣFy = 0: C y + 0.8 ( 300 N ) = 0
(b) From free-body diagram of lever BCD
∴ C y = −240 N
or
C y = 240 N
ΣFx = 0: 200 N + Cx + 0.6 ( 300 N ) = 0
2
2
2
2
C = C x + C y = ( 380 ) + ( 240 ) = 449.44 N
Then
∴ C x = −380 N
or
C x = 380 N
⎛ C y ⎞ N ⎛ − 240 ⎞
300
and ΣFy = 0: = C y −1 ⎜0.8 (⎟ = tan)−1= 0
θ tan +
⎟ = 32.276°
⎜

3. 𝑭 𝑪𝑬 =
17 26,4 4,5
= 𝟓𝟔, 𝟏 𝒌𝑵
15 2,4
𝑭 𝑪𝑬 = 𝟓𝟔, 𝟏 𝒌𝑵 𝑻 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒐 𝒆𝒏 𝒕𝒓𝒂𝒄𝒄𝒊𝒐𝒏