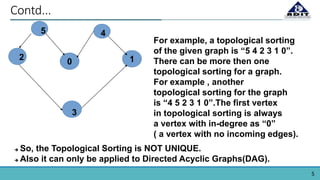
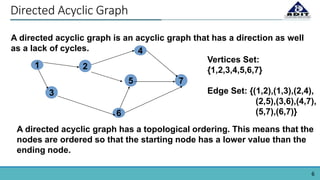
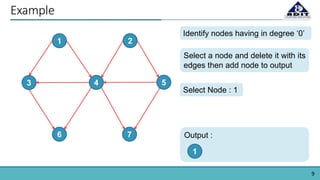
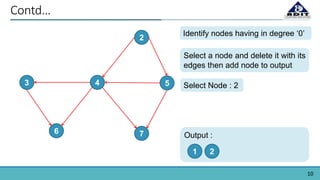
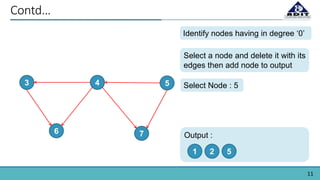
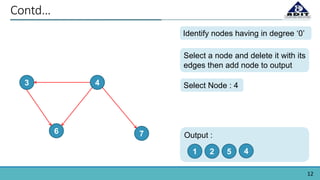
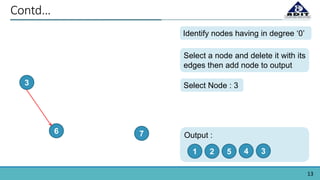
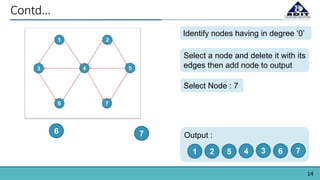
The document provides an overview of topological sorting in directed acyclic graphs (DAGs), defining it as an ordering of vertices such that for every directed edge (u, v), vertex u comes before v. It includes examples of topological sorts and outlines algorithms for identifying node order based on their in-degrees. Additionally, the document mentions applications of topological sorting in build systems, software installation in Linux, task scheduling, and managing prerequisites in educational contexts.

1. TOPOLOGICAL SORT
A. D. PATEL INSTITUTE OF TECHNOLOGY
ANALYSIS AND DESIGN OF ALGORITHMS(2150703) : A.Y. 2018-19
DEPARTMENT OF INFORMATION TECHNOLOGY
A D PATEL INSTITUTE OF TECHNOLOGY (ADIT)
NEW VALLABH VIDYANAGAR, ANAND, GUJARAT
GUIDED BY:
PROF. DINESH J. PRAJAPATI
(DEPT OF IT, ADIT)
PREPARED BY:
KUNAL R. KATHE(160010116021)
DHRUV V. SHAH (160010116053)
RUSHIL V. PATEL (160014116001)
B.E. (IT) SEM - V
8TH OCTOBER, 2018

2. 2
Outline
 Introduction
 Directed Acyclic Graph(DAG)
 Algorithm
 Example
 Applications
 References

3. 3
Introduction
WHAT IS TOPOLOGICAL SORT ?
 For a directed acyclic graph G=(V,E)
 A topological sort is an ordering of all of G’s vertices
 v1, v2, v3,….,vn such that …
 Vertex u comes before vertex v if edge (u,v) belongs to G
 So,formally for every egde (vi,vk) in E ,i<k

4. 4
Contd...
Definition:
A topological sort or topological ordering of a directed
ayclic graph is a linear ordering of its vertices such that
for every directed edge (u,v) from vertex u to v, u
comes before v in the ordering.

5. 5
Contd...
0 1
5
2
4
3
For example, a topological sorting
of the given graph is “5 4 2 3 1 0”.
There can be more then one
topological sorting for a graph.
For example , another
topological sorting for the graph
is “4 5 2 3 1 0”.The first vertex
in topological sorting is always
a vertex with in-degree as “0”
( a vertex with no incoming edges).
 So, the Topological Sorting is NOT UNIQUE.
 Also it can only be applied to Directed Acyclic Graphs(DAG).

6. 6
Directed Acyclic Graph
A directed acyclic graph is an acyclic graph that has a direction as well
as a lack of cycles.
1 2
4
3
5 7
6
Vertices Set:
{1,2,3,4,5,6,7}
Edge Set: {(1,2),(1,3),(2,4),
(2,5),(3,6),(4,7),
(5,7),(6,7)}
A directed acyclic graph has a topological ordering. This means that the
nodes are ordered so that the starting node has a lower value than the
ending node.

7. 7
Contd...

8. 8
Algorithm
1
2
3
4
5

9. 9
Example
1 2
43 5
6 7
Identify nodes having in degree ‘0’
Select a node and delete it with its
edges then add node to output
Select Node : 1
Output :
1

10. 10
Contd…
2
43 5
6 7
Identify nodes having in degree ‘0’
Select a node and delete it with its
edges then add node to output
Select Node : 2
Output :
1 2

11. 11
Contd…
43 5
6 7
Identify nodes having in degree ‘0’
Select a node and delete it with its
edges then add node to output
Select Node : 5
Output :
1 2 5

12. 12
Contd…
43
6 7
Identify nodes having in degree ‘0’
Select a node and delete it with its
edges then add node to output
Select Node : 4
Output :
1 2 5 4

13. 13
Contd…
3
6 7
Identify nodes having in degree ‘0’
Select a node and delete it with its
edges then add node to output
Select Node : 3
Output :
1 2 5 4 3

14. 14
Contd…
6 7
Identify nodes having in degree ‘0’
Select a node and delete it with its
edges then add node to output
Select Node : 6
Output :
1 2 5 4 3 6
Select Node : 7
7

15. 15
Applications
 1] Build Systems :
 We have various IDE’s like Ecllipse , Netbeans etc. We have to
build a project which has many libraries dependent on each
 other then IDE uses Topological Sort to decide which library to
 include or build first.
 2] Advanced-Packaging Tool(apt-get) :
 In Linux apt-get is used to install softwares in the system. The command
 “apt-get install VLC” is used. It is the way in Linux to install and remove
 softwares.

16. 16
Contd...
 3] Task Scheduling :
 Topological Sort is helpful in scheduling interdependent task to
know which rask should proceed which one.
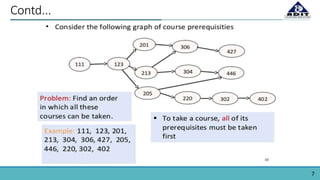
 4] Pre- Requisite Problems:
 We often come across situations where we need to finish one job in order to
 proceed the next one. For ex, In University structure, we need to complete
 basic Algorithm course to study an Advance Algorithm course. So, there
 exist a pre- requisite and we can know this by doing a topological sort on all.

17. 17
QUERY ?

18. 18