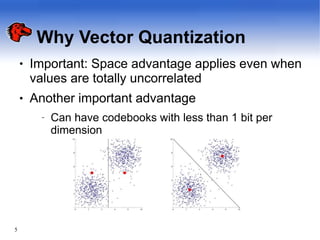
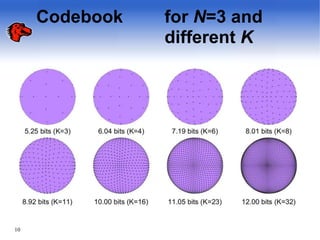
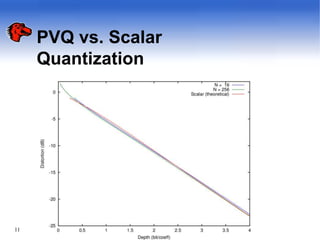
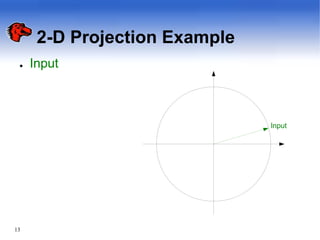
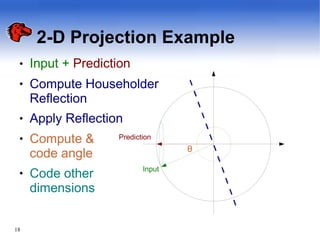
The document discusses pyramid vector quantization (PVQ), a technique for data compression. PVQ uses cubic lattice points on the surface of an L-dimensional pyramid to quantize vectors. It has simple encoding and decoding algorithms. The document analyzes the mean square error of PVQ and presents simulation results showing PVQ provides improvements in rate-distortion over scalar quantization for memoryless sources like Laplacian, gamma, and Gaussian distributions. While suboptimal, PVQ offers significant distortion reductions compared to scalar quantization and provides an alternative to other vector quantizers.

1. Pyramid vector quantization
A. D. Patel Institute of Technology
Data compression and data retrieval(2161603) : A.Y. 2018-19
Guided By:
Prof. Keyur sir
(Dept of IT, ADIT)
Prepared by:
Kunal Kathe
E.r.No.:160010116021
Shah Dhruv
E.R No.:160010116053
Rahul jadeja
E.r.No.:160010116018
B.E. (IT) Sem - VI
Department of Information Technology
A D Patel Institute of Technology (ADIT)
New Vallabh Vidyanagar, Anand, Gujarat

2. 2
What is PVQ?
The geometric properties of a memoryless Laplacian source are presented and used to
establish a source coding theorem. Motivated by this geometric structure, a pyramid vector
quantizer (PVQ) is developed for arbitrary vector dimension. The PVQ is based on the cubic
lattice points that lie on the surface of anL-dimensional pyramid and has simple encoding and
decoding algorithms. A product code version of the PVQ is developed and generalized to
apply to a variety of sources. Analytical expressions are derived for the PVQ mean square
error (mse), and simulation results are presented for PVQ encoding of several memoryless
sources. For large rate and dimension, PVQ encoding of memoryless Laplacian, gamma, and
Gaussian sources provides rose improvements of5.64, 8.40, and2.39dB, respectively, over the
corresponding optimum scalar quantizer. Although suboptimum in a rate-distortion sense,
because the PVQ can encode large-dimensional vectors, it offers significant reduction in rose
distortion compared with the optimum Lloyd-Max scalar quantizer, and provides an attractive
alternative to currently available vector quantizers.

3. Why Vector Quantization?
3
● 3 classic advantages (Lookabaugh et al. 1989):
– Space filling advantage: VQ codepoints tile space
more efficiently
●
● Example: 2-D, squares vs. hexagons
Maximum possible gain for large dimension: 1.53 dB
– Shape advantage: VQ can use more points where
PDF is higher
● 1.14 dB gain for 2-D Gaussian, 2.81 for high dimension
– Memory advantage: exploit statistical dependence
between vector components

4. Why Vector Quantization?
4
● 3 classic advantages (Lookabaugh et al. 1989):
– Space filling advantage: VQ codepoints tile
space more efficiently
●
● Example: 2-D, squares vs. hexagons
Maximum possible gain for large dimension: 1.53 dB
– Shape advantage: VQ can use more points where
PDF is higher
● Can be mitigated with entropy coding
– Memory advantage: exploit statistical dependence
between vector components
● Transform coefficients are not strongly correlated

5. Why Vector Quantization
●
●
Important: Space advantage applies even when
values are totally uncorrelated
Another important advantage
– Can have codebooks with less than 1 bit per
dimension
5

6. Why Algebraic VQ?
6
● Trained VQ impractical for high rates, large
dimensions
– High dimension → large LUTs, lots of memory
●
●
● Exponential in bitrate
– No codebook structure → slow search
“Algebraic” VQ solves these problems
– Structured codebook: no LUTs, fast search
Space-filling lattice for arbitrary dimension
unknown: have to approximate
– PVQ asymptotically optimal for Laplacian sources

7. Why Gain-Shape
Quantization?
7
●
●
Separate “gain” (energy) from “shape” (spectrum)
– Vector = Magnitude × Unit Vector (point on sphere)
Potential advantages
– Can give each piece different rate allocations
●
● Preserve energy (contrast) instead of low-passing
Scalar can only add energy by coding ±1’s
– Implicit activity masking
● Can derive quantization resolution from the
explicitly coded energy
– Better representation of coefficients

8. How it Works (High-Level)
8

9. Simple Case: PVQ without a
Predictor
●
●
Scalar quantize gain
Place K unit pulses in N dimensions
– Up to N = 1024 dimensions for large blocks
– Only has N-1 degrees of freedom
●
●
●
Normalize to unit norm
K is derived implicitly from the gain
Can also code K and derive gain
9

10. Codebook for N=3 and
different K
10

11. PVQ vs. Scalar
Quantization
11

12. PVQ with a Predictor
12
●
●
●
●
Video provides us with useful predictors
We want to treat vectors in the direction of the
prediction as “special”
– They are much more likely!
Subtracting and coding the residual would lose
energy preservation
Solution: align the codebook axes with the
prediction, and treat one dimension differently

13. 2-D Projection Example
Input
13
● Input

14. 2-D Projection Example
Prediction
Input
14
● Input + Prediction

15. 2-D Projection Example
Prediction
Input
15
●
●
Input + Prediction
Compute Householder
Reflection

16. 2-D Projection Example
Input
●
16
●
●
Input + Prediction
Compute Householder
Reflection
Apply Reflection
Prediction

17. 2-D Projection Example
θ
Prediction
Input
●
17
●
●
Input + Prediction
Compute Householder
Reflection
Apply Reflection
● Compute &
code angle

18. 2-D Projection Example
●
●
●
Input + Prediction
Compute Householder
Reflection
Apply Reflection
●
●
Compute &
code angle
Code other
dimensions
Prediction
Input
θ
18