This document describes a web-based application called "Path Finding Visualizer" that visualizes shortest path algorithms like Dijkstra's algorithm and A* algorithm. It discusses the motivation, objectives and implementation of the project. The implementation involves creating a graph from a maze, building an adjacency matrix to represent the graph, and applying Dijkstra's algorithm to find the shortest path between nodes. Screenshots show the visualization of Dijkstra's algorithm finding the shortest path between a source and destination node. The technologies used include Visual Studio Code. The project aims to help users better understand how shortest path algorithms work through visualization.

1. CricScorer
Department of Information Technology
Aldel Education Trust’s
St. John College of Engineering and Management, Palghar
NAAC Accredited with Grade A (2017-2022)
SHORTEST PATH VISUALIZER
KAVISH GHAG [EU1214032]
HARDIK PAWAR [EU1214036]
AKANSH SINGH [EU1214050]
KUNAL GAIKWAD [EU1214051]
DR. ARUN SAXENA| Project Guide
November 5, 2022
1

2. Contents
• Introduction
❑ Motivation
❑ Problem Statement
❑ Objectives
❑ Scope
• Review of Existing Literature
• Proposed System
❑ Block diagram of Proposed System
• Implementation
❑ Algorithm/Flowchart
❑ Screenshots of the output with description
• Technologies Used
• Results and Discussion
• Conclusion and Future Work
• References
2

3. Abstract
▪ Visualization is an efficient way of learning any concept
faster than conventional methods. Modern technology
allows creating e-Learning tools that also helps in
improving computer science education very much. The
goal of this project is to create a web based e-Learning
tool, ‘Path Finding Visualizer’, which can be used to
visualize shortest path algorithms. The conceptual
application of the project is illustrated by implementation
of algorithms like Dijkstra’s , A* and DFS.
3

4. Introduction
4
Path finding algorithms are important because they
are used in applications like google maps, satellite navigation
systems, routing packets over the internet. The usage of path
finding algorithms isn’t just limited to navigation systems. The
overarching idea can be applied to other applications as well.
• Motivation:

5. • Problem Statement:
5
Introduction
In graph theory, the shortest path problem is the
problem of finding a path between two vertices (or nodes)
in a graph such that the sum of the weights of its
constituent edges is minimized. The problem of finding the
shortest path between two intersections on a road map
may be modeled as a special case of the shortest path
problem in graphs, where the vertices correspond to
intersections and the edges correspond to road segments,
each weighted by the length of the segment.

6. • Objectives:
Path finding algorithms are important because they
are used in applications like google maps, satellite
navigation systems, routing packets over the internet. The
usage of path-finding algorithms isn’t just limited to
navigation systems. The overarching idea can be applied to
other applications as well.
6
Introduction

7. • Scope:
Path-finding is an integral part of nearly all the
computer related technologies, be it, routing of IP Packets,
Computer Games, GPS or Robotics. As the population
grows and demand for such technologies will rise
exponentially in the near future. Thus, it is only natural for
there to be constant need to optimize the path-finding
algorithms to keep up with the ever changing and ever-
evolving needs. And since, most of the applications of
Path-Finding are real-time, there has to be a way to deal
with the dynamic changes in the every topology and life-
span, and for this, optimization of the current available
algorithms is a must.
7
Introduction

8. Literature Review
Sr.
No.
year Title Author Advantages Disadvantages
1
2
3
4
8

9. Proposed System
10

10. Implementation
1
Implementation is divided into subparts which includes :
(1) Making level on the board
(2) Building Adjacency/Connectivity Matrix of 1275 x 1275
dimensions where 1275 (= 25 x 51) are number of nodes in the
graph.
(3) Applying dijkstra algo whose input is matrix, source point and
destination point and output is shortest path from source to
destination and shortest distance from source to destination.

11. 12
Implementation
(1)Making level on board
- Green Start button is to make box
green one, Red End button is for
making destination box and grey
button is used to make walls.
- Sample maze is shown on the right
hand side

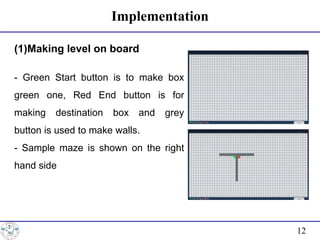
12. Implementation
(2) Building Adjacency Matrix
- Our 1275 nodes(buttons) will make matrix of 1275 x
1275 dimensions. Each element of matrix adj[i][j]
represents some information.
- Adj[i][j] means element of ith row and jth column and if
adj[i][j] is 1 then node ‘i’ is connected to node ‘j’ and if it is
0 then node ‘i’ and ‘j’ are not connected.

13. Implementation
(3) Dijkstra’s Algorithm Implementation
(1) It all starts with source node where algorithm starts its
implementation.
(2) Algorithm will search for its neighbours from current
node and check its distance and will store its distance
if it is less than currently stored distance and hence
taking the shortest branch of the current node.
(3) And when it reaches the destination it starts
backtracking from where it came and hence prints the
path

14. Implementation
Data type named Element is made which contains
following members:
- Int data(stores traversed distance)
- Int Distance Of(stores node number of which we are
checking for)
- Int via (stores node number from where we are coming)
- Int priority(not accessible because it is set
automatically)

15. Implementation
Visualisation of Implementation (Src=1, Dest.=4)
When algo is on source queue will be like
[[[Element{data = 0, distanceOf = 1, via = -1, priority = 0}]]]
It is then dequeued and is checked for neighbours and set
as follows.
[[[Element{data = 1, distanceOf = 2, via = 1, priority = 0}
Element{data = 1, distanceOf = 3, via = 1, priority = 1}]]]

16. Implementation
• Stack when node = 1 (At Source) Stack will be
(((Element{data = 1, distanceOf = 2, via = 1} Element{data = 0,
distanceOf = 1, via = -1})))
• Queue when current node = 2
[[[Element{data = 1, distanceOf = 3, via = 1, priority = 0}
Element{data = 2, distanceOf = 4, via = 2, priority = 1}]]]
• Stack when current node = 2
((( Element{data = 2, distanceOf = 4, via = 2}
Element{data = 1, distanceOf = 2, via = 1}
Element{data = 0, distanceOf = 1, via = -1} )))
• Backtracking Takes Place
pathArray = [4, 2, 1] (Destination -> Source) path Distance = 2

17. Technologies Used
∙ Hardware Requirements:
a. Hard Disk – 1 TB.
b. RAM required – 8GB (minimum)
c. Processor – Intel Core i5 8th Gen
∙ Software Requirements:
a. Visual Studio Code
20

18. Results and Discussion
The main aim for creating this web based application for
visualizing various path-finding algorithms and randomized
maze generation algorithms was to develop a utility than
can help those who find it difficult to understand how
various path-finding algorithms like Dijkstra’s Algorithm or
A* Algorithm works in tracing the shortest path between a
start node and a destination node. The algorithms
implemented in this project does not all provide the shortest
paths between two nodes, but they demonstrate how
different algorithm will trace and get better insights from the
surrounding node in order to find the best possible shortest
path as per it’s logic and algorithm.
21

19. Conclusion
• Conclusion:
• The main aim for creating this web based application for
visualizing various path-finding algorithms and randomized
maze generation algorithms was to develop a utility than can
help those who find it difficult to understand how various
path-finding algorithms like Dijkstra’s Algorithm or A*
Algorithm works in tracing the shortest path between a start
node and a destination node.
22

20. References
1) [1]. "7.2.1 Single Source Shortest Paths Problem: Dijkstra's
Algorithm". Archived from the original on 2016-03-04.
2) [2]. Delling, D.; Sanders, P.; Schultes, D.; Wagner, D. (2009).
"Engineering route planning algorithms". Algorithmics of
Large and Complex Networks: Design, Analysis, and
Simulation. Lecture Notes in Computer Science. 5515.
Springer. pp. 117–139.
3) [3]. Crawford, Chris (December 1982). "Design Techniques
and Ideas for Computer Games". BYTE. p. 96. Retrieved 19
October 2013.
4) [4]. Holte, Robert C and Perez, MB and Zimmer, RM and
MacDonald, AJ (1995). Hierarchical a*. Symposium on
Abstraction, Reformulation, and Approximation.
23

21. Future Work
Path-finding is an integral part of nearly all the computer
related technologies, be it, routing of IP Packets,
Computer Games, GPS or Robotics. As the population
grows and demand for such technologies will rise
exponentially in the near future.Thus, it is only natural for
there to be constant need to optimize the path-finding
algorithms to keep up with the ever changing and ever-
evolving needs.
And since, most of the applications of Path-Finding are
real-time, there has to be a way to deal with the dynamic
changes in the every topology and life-span, and for this,
optimization of the current available algorithms is a must.

22. Thank You !!!
24

23. Q & A
25