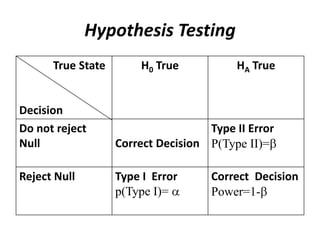
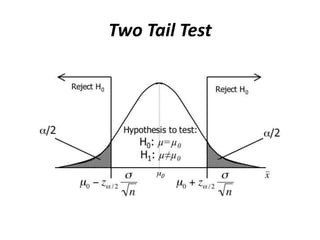
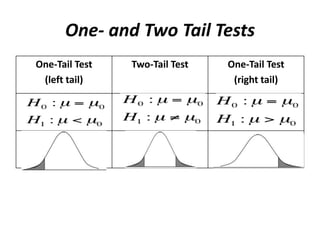
The document discusses statistical hypothesis testing. It defines key terms like the null hypothesis, alternative hypothesis, test statistic, rejection region, Type I and Type II errors, significance level, and p-value. It also describes the steps to conduct a hypothesis test including stating the hypotheses, choosing a test statistic, determining critical values, and interpreting the conclusions. Specific hypothesis tests for a population mean are also covered, including tests when the population variance is known versus unknown.

1. Statistical Inference

2. Hypothesis Testing
• What is a statistical hypothesis?
• What is so important about it?
• What is a rejection region?
• What does it mean to say that a finding is
statistically significant?
• Describe Type I and Type II errors.

3. Hypothesis Testing
• Task: Statement about unknown vales of population
parameters in terms of sample information
• Elements of a hypothesis test:
– Null hypothesis (H0 ) - Statement on the value(s) of unknown
parameter(s);
– Alternative hypothesis - Statement contradictory to the null
hypothesis
– Test statistic – Estimate based on sample information and null
hypothesis used to test between null and alternative
hypotheses
– Rejection (Critical) region – Range of value on the test statistic
for which we reject the null in favor of the alternative
hypothesis

4. Hypothesis Testing
True State H0 True HA True
Decision
Do not reject Type II Error
Null Correct Decision P(Type II)=
Reject Null Type I Error Correct Decision
p(Type I)= Power=1-

5. Critical Value
• Critical value: Value that separates the
critical (rejection) region from the
values of the test statistic that do not
lead to rejection of the null hypothesis,
given the sampling distribution and the
significance level .

6. Significance Level
• The significance level ( ): Probability of
the test statistic falling in the critical
region under a valid null hypothesis.
• : Conventional Choices for are 0.05,
0.01, and 0.10.
• p-value: Probability of observing the
test statistic under the null hypothesis

7. Significance Level and Power
• Level of significance: Probability that the test
rejects the null hypothesis on the assumption
that the null hypothesis is true.
• Power of a test: Probability that that the test
rejects the null hypothesis on the assumption
that that alternative hypothesis is true.

8. Test of Hypothesis: Interpretations
• Rejecting the null hypothesis
• Do not reject H0 : Does not mean that H0 is true;
nor that the data supports H0.If the observations
are few, the test would not have the power, that
is, difficult for a test to reject a false null H0.
• Reject H0 does not mean that HA is true. It
means that either H0 is false or the event has
probability no larger than the significance level.

9. Statistical Significance vs. Practical
Importance
• An effect may be of importance but not
statistically significant because of sample
limitations (poor quality or few
observations).
• The effect may not be of much policy
significance in terms of impact but still
statistically significant due to high quality of
data.

10. Hypothesis Testing: Steps
• State the maintained hypothesis.
• State the null & alternative hypotheses.
• Choose the test statistic and estimate its value.
• Specify the sampling distribution of the test
statistics under the null hypothesis.
• Determine the critical value(s) corresponding to
a significance level.
• Determine the p-value for the test statistic.
• State the conclusion of a hypothesis test in
simple, nontechnical terms.

11. Hypothesis Testing: Rationale
• We infer that the assumption is probably
incorrect given the maintained and null
hypotheses, if the probability of getting the
sample is exceptionally small.
• Please note that the null hypothesis contains
equality. Comparing the assumption and the
sample results, we infer one of the
following:

12. Hypothesis Testing: Rationale
• Under the null hypothesis, if the probability
of observing the sample estimate is
high, discrepancy between the assumption
and the sample estimate, if any, is due to
chance.
• If this probability is very low, even relatively
large discrepancy between the assumption
and the sample is due to invalid null
hypothesis.

13. Test of Hypothesis: Population Means
• Assumptions:
1) Simple random sample
2) Population variance is known
3) Population distribution is normal or sample
size is more than 30

14. Test of Hypothesis: Population Means
Known population variance
• Test statistic
x – µx
z=
n

15. Two Tail Test

16. One- and Two Tail Tests
One-Tail Test Two-Tail Test One-Tail Test
(left tail) (right tail)

17. Test of Hypothesis: Population Means
• Assumptions:
1) Simple random sample
2) Population variance is unknown
3) Population distribution is normal or sample
size is more than 30

18. Test of Hypothesis: Population Means
Unknown population variance
• Test statistic
x –µx
t= s
n

19. Student’s t-test: An Illustration
• Question: The diameter of some ball for
study is specified to be one meter. A random
sample of 10 such balls is selected to check
the specification. The sample selected gave
the following
measurements:1.01, 1.01, 1.02, 1.00, 0.99, 0.
99, 1.02, 1.02, 1.00, 1.02
• Is there any reason to believe that there has
been a change in the average diameter?

20. Student’s t-test
• Level of significance = 0.05
• Maintained hypothesis: Distribution of
diameters is normal
• n = 10
• H0 : m = 1.0
• HA : m <> 1.0
• Sample mean = 1.008

21. Student’s t-test
• Estimate of population variance = 0.000151
• Std. deviation = 0.012288
• t-statistic = 1.953125 (9 d.f.)
• t(9,0.05) = 2.262
• Computed t < tabulated t
• Do not reject H0
• Conclusion: Sample information supports the
hypothesis that the average diameter of the ball
is one meter.

22. What would be the sampling
distribution of a sample mean from
a normally distributed population?
Sample mean from a normal
population will also be normally
distributed for any sample size n

23. Central Limit Theorem
• The sampling distribution of mean of n
sample observations from any population
would be approximately normal when n is
sufficiently large.