This document discusses algorithms for order statistics and selection problems. It begins by defining order statistics as the ith smallest element of a set, with the minimum being the 1st order statistic and maximum being the nth. It then discusses algorithms for finding the minimum and maximum of a set in linear time. It introduces the selection problem of finding the element that is larger than exactly i-1 other elements and describes algorithms for solving it in expected and worst-case linear time through partitioning around a pivot element.

1. Top School in Noida
BY:
SCHOOL.EDHOLE.COM

2. Comp 122, Spring 2004
Order Statistics
school.edhole.com

3. Order Statistic
ith order statistic: ith smallest element of a set of n
elements.
Minimum: first order statistic.
Maximum: nth order statistic.
Median: “half-way point” of the set.
 Unique, when n is odd – occurs at i = (n+1)/2.
 Two medians when n is even.
 Lower median, at i = n/2.
 Upper median, at i = n/2+1.
 For consistency, “median” will refer to the lower median.
school.edhole.com
Comp 122

4. Selection Problem
Selection problem:
 Input: A set A of n distinct numbers and a number i, with 1£
i £ n.
 Output: the element x Î A that is larger than exactly i – 1
other elements of A.
Can be solved in O(n lg n) time. How?
We will study faster linear-time algorithms.
 For the special cases when i = 1 and i = n.
 For the general problem.
school.edhole.com
Comp 122

5. Minimum (Maximum)
Comp 122
Minimum (A)
1. min ¬ A[1]
2. for i ¬ 2 to length[A]
3. do if min > A[i]
4. then min ¬ A[i]
5. return min
Minimum (A)
1. min ¬ A[1]
2. for i ¬ 2 to length[A]
3. do if min > A[i]
4. then min ¬ A[i]
5. return min
Maximum can be determined similarly.
• T(n) = Q(n).
• No. of comparisons: n – 1.
• Can we do better? Why not?
• Minimum(A) has worst-school.edhole.com case optimal # of comparisons.

6. Problem
Average for random input:
Minimum (A)
1. min ¬ A[1]
2. for i ¬ 2 to length[A]
3. do if min > A[i]
4. then min ¬ A[i]
5. return min
How many times
do we expect line 4
to be executed?
 X = RV for # of executions of line 4.
 Xi = Indicator RV for the event that line 4 is executed on the ith
iteration.
 X = Si=2..n Xi
 E[Xi] = 1/i. How?
 Hence, E[X] = ln(n) – 1 = Q(lg n).
Comp 122
Minimum (A)
1. min ¬ A[1]
2. for i ¬ 2 to length[A]
3. do if min > A[i]
4. then min ¬ A[i]
5. return min
school.edhole.com

7. Simultaneous Minimum and Maximum
Some applications need to determine both the
maximum and minimum of a set of elements.
 Example: Graphics program trying to fit a set of points onto a
rectangular display.
Independent determination of maximum and
minimum requires 2n – 2 comparisons.
Can we reduce this number?
 Yes.
school.edhole.com
Comp 122

8. Simultaneous Minimum and Maximum
Maintain minimum and maximum elements seen
so far.
Process elements in pairs.
 Compare the smaller to the current minimum and the
larger to the current maximum.
 Update current minimum and maximum based on the
outcomes.
No. of comparisons per pair = 3. How?
No. of pairs £ ën/2û.
 For odd n: initialize min and max to A[1]. Pair the
remaining elements. So, no. of pairs = ën/2û.
 For even n: initialize min to the smaller of the first pair
and max to the larger. So, remaining no. of pairs = (n –
2)/2 < ën/2û.
school.edhole.com
Comp 122

9. Simultaneous Minimum and Maximum
Total no. of comparisons, C £ 3ën/2û.
 For odd n: C = 3ën/2û.
 For even n: C = 3(n – 2)/2 + 1 (For the initial comparison).
Comp 122
= 3n/2 – 2 < 3ën/2û.
school.edhole.com

10. General Selection Problem
Seems more difficult than Minimum or Maximum.
 Yet, has solutions with same asymptotic complexity as
Minimum and Maximum.
We will study 2 algorithms for the general problem.
 One with expected linear-time complexity.
 A second, whose worst-case complexity is linear.
school.edhole.com
Comp 122

11. Selection in Expected Linear Time
Modeled after randomized quicksort.
Exploits the abilities of Randomized-Partition (RP).
 RP returns the index k in the sorted order of a randomly
chosen element (pivot).
 If the order statistic we are interested in, i, equals k, then we are
done.
 Else, reduce the problem size using its other ability.
 RP rearranges the other elements around the random
pivot.
 If i < k, selection can be narrowed down to A[1..k – 1].
 Else, select the (i – k)th element from A[k+1..n].
(Assuming RP operates on A[1..n]. For A[p..r], change k
schooaplp.erodphriaotelely..)com
Comp 122

12. Randomized Quicksort: review
Partition 5
school.edhole.com
Comp 122
Quicksort(A, p, r)
Quicksort(A, p, r)
if p < r then
if p < r then
q := Rnd-Partition(A, p, r);
Quicksort(A, p, q – 1);
Quicksort(A, q + 1, r)
fi
q := Rnd-Partition(A, p, r);
Quicksort(A, p, q – 1);
Quicksort(A, q + 1, r)
fi
Rnd-Partition(A, p, r)
Rnd-Partition(A, p, r)
i := Random(p, r);
A[r] « A[i];
x, i := A[r], p – 1;
for j := p to r – 1 do
i := Random(p, r);
A[r] « A[i];
x, i := A[r], p – 1;
for j := p to r – 1 do
if A[j] £ x then
if A[j] £ x then
i := i + 1;
A[i] « A[j]
i := i + 1;
A[i] « A[j]
fi
fi
od;
A[i + 1] « A[r];
return i + 1
od;
A[i + 1] « A[r];
return i + 1
5
A[p..r]
A[p..q – 1] A[q+1..r]
£ 5 ³ 5

13. Randomized-Select
Randomized-Select(A, p, r, i) // select ith order statistic.
1. if p = r
2. then return A[p]
3. q ¬ Randomized-Partition(A, p, r)
4. k ¬ q – p + 1
5. if i = k
6. then return A[q]
7. elseif i < k
8. then return Randomized-Select(A, p, q – 1, i)
9. else return Randomized-Select(A, q+1, r, i – k)
Randomized-Select(A, p, r, i) // select ith order statistic.
1. if p = r
2. then return A[p]
3. q ¬ Randomized-Partition(A, p, r)
4. k ¬ q – p + 1
5. if i = k
6. then return A[q]
7. elseif i < k
8. then return Randomized-Select(A, p, q – 1, i)
9. else return Randomized-Select(A, q+1, r, i – k)
Comp 122

14. Analysis
Worst-case Complexity:
 Q(n2) – As we could get unlucky and always recurse on a
subarray that is only one element smaller than the previous
subarray.
Average-case Complexity:
 Q(n) – Intuition: Because the pivot is chosen at random, we
expect that we get rid of half of the list each time we choose a
random pivot q.
 Why Q(n) and not Q(n lg n)?
school.edhole.com
Comp 122

15. Average-case Analysis
Define Indicator RV’s Xk, for 1 £ k £ n.
 Xk = I{subarray A[p…q] has exactly k elements}.
 Pr{subarray A[p…q] has exactly k elements} = 1/n for all k = 1..n.
 Hence, E[Xk] = 1/n.
Let T(n) be the RV for the time required by
Randomized-Select (RS) on A[p…q] of n elements.
Determine an upper bound on E[T(n)].
Comp 122
(9.1)
school.edhole.com

16. Average-case Analysis
A call to RS may
 Terminate immediately with the correct answer,
 Recurse on A[p..q – 1], or
 Recurse on A[q+1..r].
To obtain an upper bound, assume that the ith
smallest element that we want is always in the larger
subarray.
RP takes O(n) time on a problem of size n.
Hence, recurrence for T(n) is:

n
T n Xk T k n k O n
( ) ( (max( 1, )) ( ))
For a given call of RS, Xk =1 for exactly one value of
k, and Xk = 0 for all other k.
Comp 122
å=
£ × - - +
k
1
school.edhole.com

17. Average-case Analysis
å
T n £ X × T k - n - k +
O n
( ) ( (max( 1, )) ( ))
X T k n k O n
= × - - +
(max( 1, )) ( )
=
1
Taking expectation, we have
£ é × - - +
E T n E X T k n k O n
[ ( )] (max( 1, )) ( )
Comp 122
E X T k n k O n
= × - - +
ù
[ (max( 1, ))] ( )
E X E T k n k O n
= × - - +
[ ] [ (max( 1, ))] ( )
1 [ (max( 1, ))] ( )
å
=
1
å
=
1
1
1
1
å
å
å
=
=
=
= × - - +
úû
êë
n
k
n
k
k
n
k
k
n
k
k
n
k
k
n
k
k
E T k n k O n
n
(by linearity of expectation)
(by Eq. (C.23))
school.edhole.com (by Eq. (9.1))

18. Average-case Analysis (Contd.)
Comp 122
k k n
1 if / 2
é ù
é ù
- >
if / 2
The summation is expanded
E T n E T n E T n n
n
- + - + + - +
1 ( ( 1)) ( ( 2)) ( ( / 2 )) [ ( )] ( )
é ù
ö
é ù ÷ ÷ø
æ
ç çè
+ + -
£ +
î í ì
- £
- - =
( ( / 2 )) ( ( 1))
max( 1, )
E T n E T n
E T n O n
n k k n
k n k


• If n is odd, T(n – 1) thru T(én/2ù) occur twice and T(ën/2û) occurs once.
• If n is even, T(n – 1) thru T(én/2ù) occur twice.
[ ( )] 2 [ ( )] ( ).
å-
£ +
ë û
=
1
/ 2
Thus, we have
n
k n
E T k O n
n
E T n

19. Average-case Analysis (Contd.)
We solve the recurrence by substitution.
Guess E[T(n)] = O(n).
[ ( )] 2
Comp 122
å
ck an
£ +
ë û
ë û
n
c
n
æ
æ
-
1
å å
k k an
1
n n an
c
n
3
c n
1
3
= æ + -
ö n
çè
cn c an
£ + +
+ ÷ø
ö
an
4 2
ö çè
÷ø
= - æ - -
+ ÷ ÷ø ö
ç çè
£ + -
+ ÷ ÷ø
ç çè
= -
=
-
=
-
=
cn cn c an
E T n
n
k
n
k
n
k n
4 2
3
2
2
4
2
4 2
2
2
/ 2 1
1
1
/ 2
cn cn c an cn
ö çè
cn c an
Þ - - ³
n c a c
Þ - ³
( / 4 ) / 2, or
c
, if 4 .
4
2
/ 2
n c
/ 4
0
4 2
,
4 2
c a
c a
c a
>
-
=
-
³
£ ÷ø
- æ - -
Thus, if we assume T(n) = O(1) for
n < 2c/(c – 4a), we have E[T(n)] =
school.edhole.com O(n).

20. Selection in Worst-Case Linear Time
Algorithm Select:
 Like RandomizedSelect, finds the desired element by
recursively partitioning the input array.
 Unlike RandomizedSelect, is deterministic.
 Uses a variant of the deterministic Partition routine.
 Partition is told which element to use as the pivot.
 Achieves linear-time complexity in the worst case by
 Guaranteeing that the split is always “good” at each Partition.
 How can a good split be guaranteed?
school.edhole.com
Comp 122

21. Guaranteeing a Good Split
We will have a good split if we can ensure that the
pivot is the median element or an element close to the
median.
Hence, determining a reasonable pivot is the first
step.
school.edhole.com
Comp 122

22. Choosing a Pivot
Median-of-Medians:
 Divide the n elements into én/5ù groups.
 ë n/5û groups contain 5 elements each. 1 group contains n mod 5
< 5 elements.
 Determine the median of each of the groups.
Comp 122
 Sort each group using Insertion Sort. Pick the median from the
sorted list of group elements.
 Recursively find the median x of the én/5ù medians.
Recurrence for running time (of median-of-medians):
 T(n) = O(n) + T(én/5ù) + ….
school.edhole.com

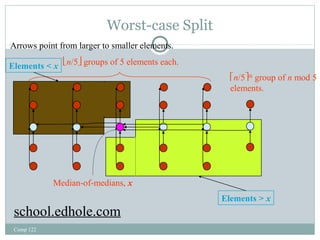
23. Algorithm Select
Determine the median-of-medians x (using the
procedure on the previous slide.)
Partition the input array around x using the variant
of Partition.
Let k be the index of x that Partition returns.
If k = i, then return x.
Else if i < k, then apply Select recursively to A[1..k–1]
to find the ith smallest element.
Else if i > k, then apply Select recursively to
A[k+1..n] to find the (i – k)th smallest element.
(Assumption: Select operates on A[1..n]. For subarrays A[p..r],
sscuhitoaoblly.e cdhhanoglee .kc. o)m
Comp 122

24. Worst-case Split
Comp 122
ën/5û groups of 5 elements each.
Median-of-medians, x
én/5ùth group of n mod 5
elements.
Arrows point from larger to smaller elements.
Elements > x
Elements < x
school.edhole.com

25. Worst-case Split
Assumption: Elements are distinct. Why?
At least half of the én/5ù medians are greater than
x.
Thus, at least half of the én/5ù groups contribute 3
elements that are greater than x.
 The last group and the group containing x may contribute
fewer than 3 elements. Exclude these groups.
Hence, the no. of elements > x is at least
én n
úú
æ - ö çè
3 é
1 ù
2 ÷ø
³ 3
- Analogously, the no. of elements < x is at least
3n/10–6.
Thus, in the worst case, Select is called recursively
on at most 7n/10+6 elements.
Comp 122
6
10
2 5
ù
êê
úú
êê
school.edhole.com

26. Recurrence for worst-case running time
T(Select) £ T(Median-of-medians) +T(Partition)
+T(recursive call to select)
T(n) £ O(n) + T(én/5ù) + O(n) + T(7n/10+6)
Comp 122
T(Median-of-medians) T(Partition) T(recursive call)
= T(én/5ù) + T(7n/10+6) + O(n)
Assume T(n) £ Q(1), for n £ 140.
school.edhole.com

27. Solving the recurrence
To show: T(n) = O(n) £ cn for suitable c and all n > 0.
Assume: T(n) £ cn for suitable c and all n £ 140.
Substituting the inductive hypothesis into the recurrence,
 T(n) £ c én/5ù + c(7n/10+6)+an
Comp 122
£ cn/5 + c + 7cn/10 + 6c + an
= 9cn/10 + 7c + an
= cn +(–cn/10 + 7c + an)
£ cn, if –cn/10 + 7c + an £ 0.
–cn/10 + 7c + an £ 0 º c ³
10a(n/(n – 70)), when n >
70.
For n ³ 140, c ³ 20a.
n/(n–70) is a decreasing function of n. Verify.
Hence, c can be chosen for any n = n> 70, provided it can
0 be school.assumed edhole.that com
T(n) = O(1) for n £ n.
0Thus, Select has linear-time complexity in the worst case.