This document summarizes the design and implementation of parallel and randomized approximation algorithms for solving matrix games, linear programs, and semi-definite programs. It presents solvers for these problems that provide approximate solutions in sublinear or near-linear time. It analyzes the performance and precision-time tradeoffs of the solvers compared to other algorithms. It also provides examples of applying the SDP solver to approximate the Lovasz theta function.

1. Design and Implementation of Parallel and
Randomized Approximation Algorithms
by
Ajay Shankar Bidyarthy
(b.ajay@iitg.ernet.in)
Under the Guidance of
Dr. Gautam K. Das
Department of Mathematics
Indian Institute of Technology Guwahati
Guwahati - 781039, India
November 26, 2012

2. Topics
Matrix Games solver
Linear Programs solver
Semi-Definite Programs solver
Example: Lovasz ϑ function
Results
Conclusions
Future Works

3. Matrix Games solver
The problem is to compute an x such that
Ax ≤ e, x ∈ S = {x ∈ Rn|e x = 1, x ≥ 0}
where
A is the payoff matrix
A = −A
Elements of A lie in [−1, 1]
∈ (0, 1]
n ≥ 8

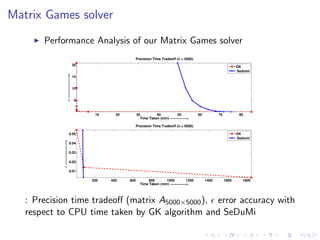
4. Matrix Games solver
Our solver returns
x ∈ Rn
, an optimal strategy vector for A
with probability ≥ 1/2
Time complexity
O( 1
2 log2
n) expected time on an n/ log n-processor [Khachiyan
et al. [5]] (we will refer it by GK)
Our solver takes O( 1
2 n log n) at most time on single processor

5. Matrix Games solver
Performance Analysis of our Matrix Games solver
10 20 30 40 50 60 70 80
5
10
15
20
ε−−−−−−−−−−−>
Time Taken (min) −−−−−−−−>
Precision Time Tradeoff (n = 5000)
GK
Sedumi
200 400 600 800 1000 1200 1400 1600 1800
0.01
0.02
0.03
0.04
0.05
ε−−−−−−−−−−−>
Time Taken (min) −−−−−−−−>
Precision Time Tradeoff (n = 5000)
GK
Sedumi
: Precision time tradeoff (matrix A5000×5000), error accuracy with
respect to CPU time taken by GK algorithm and SeDuMi

6. Linear Programs solver
LP of the form
Packing:
max{|x| : Ax ≤ 1, x ≥ 0}
Covering:
min{|ˆx| : A ˆx ≥ 1, ˆx ≥ 0}
Note: Coefficients of xj ’s and bi ’s are one, for i = 1, 2, ..., r
and j = 1, 2, ..., c.
where
Elements of the constraint matrix A lie in [0, 1]r×c
r and c is number of rows and column respectively

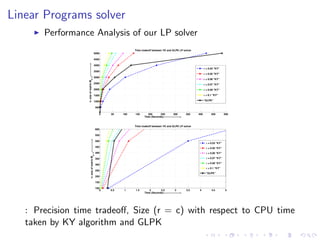
7. Linear Programs solver
Our solver returns
A (1 − 2 ) - approximate feasible primal-dual pair x and ˆx
|x | ≥ (1 − 2 )|ˆx | [Christos et al. [6]] (We will refer it by KY)
with probability at least 1 − 1/(rc)
∈ (0, 1]
Time complexity
Our solver takes O( 1
2 n log n) at most time on single processor

8. Linear Programs solver
Performance Analysis of our LP solver
0 50 100 150 200 250 300 350 400 450 500
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
Time (Seconds)−−−−−−−−−−−>
n:sizeofmatrixMn×n
−−−−−−−−>
Time tradeoff between YK and GLPK LP solver
ε = 0.03 "KY"
ε = 0.05 "KY"
ε = 0.06 "KY"
ε = 0.07 "KY"
ε = 0.09 "KY"
ε = 0.1 "KY"
"GLPK"
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
100
150
200
250
300
350
400
450
500
550
600
Time (Seconds)−−−−−−−−−−−>
n:sizeofmatrixMn×n
−−−−−−−−>
Time tradeoff between YK and GLPK LP solver
ε = 0.03 "KY"
ε = 0.05 "KY"
ε = 0.06 "KY"
ε = 0.07 "KY"
ε = 0.09 "KY"
ε = 0.1 "KY"
"GLPK"
: Precision time tradeoff, Size (r = c) with respect to CPU time
taken by KY algorithm and GLPK

9. Semi-Definite Programs
Semidefinite programming (SDP) solves the following
problem:
min A0 • X
subject to Aj • X ≥ bj for j = 1, 2, ..., m
X 0.
Where
X ∈ Rn×n
is a matrix of variables
A1, A2, ..., Am ∈ Rn×n
For n × n matrices A and B, A • B = ij Aij Bij
A 0 is notation for A is PSD

10. Semi-Definite Programs: feasibility engine algorithm
On input ( An×n
j , bj for j = 1, 2, ..., m, , R ( i Xii ≤ R))
Result: Feasible/infeasible solution PSD matrix X
Initialize wj s.t. j wj = 1, iter = n log n
2 , β = min{2, 0.01}.
while T < iter do
Update T: T = T + 1.
Compute C: C = m
j=1 w
(t)
j (Aj −
bj
R I).
if C is negative definite report solution is infeasible and
stop, else compute the largest eigenvector of C say V .
Compute Xt: Xt = V × V
Update Wj : w
(t+1)
j = w
(t)
j (1 − β(Aj • Xt − bj ))/St, where
St = m
j=1 w
(t)
j (1 − β(Aj • Xt − bj )).
end
Compute X: X = T
t=1
Xt
T and return X.algo1
Algorithm 1: Decision making algorithm for primal only SDP
using multiplicative weights update method

11. Semi-Definite Programs: Algorithm correctness
Objective, the SDP problem P is to be solved.
1. Solve P using the feasibility engine. Let output be K
constraints feasible
2. Solve P using SDPA, SeDuMi and etc. with exactly K
constraints and an A0 objective. Let output be α .
3. Give P return back to the feasibility engine with exactly K
constraints + A0 • X ≥ α ± δ, for small δ > 0
feasibility engine should return K constraints feasible and
A0 • X ≥ α − δ : feasible (satisfiable) and
A0 • X ≥ α + δ : infeasible (not satisfiable).

12. Semi-Definite Programs: Example
Let n = 2, m = 3, A0 =
−11 0
0 23
, A1 =
10 4
4 0
,
A2 =
0 0
0 −8
, A3 =
0 −8
−8 −2
, b =


−48
−8
−20


Step 1: feasibility engine output K = 3
Step 2: SDPA, SeDuMi etc. output
objValPrimal = +2.3000000262935881e + 01
objValDual = +2.2999999846605416e + 01
Step 3: for n = 2, m = 3 + 1 = K + 1, = 0.01, R ≥ 11, (since
Tr(X) ≤ R, δ = 0.01 and α = 23.0,
feasibility engine output
A0 • X ≥ α + δ : infeasible (not satisfiable)
A0 • X ≥ α − δ : feasible (satisfiable)

13. Semi-Definite Programs
Performance Analysis of our SDP solver
100 200 300 400 500 600 700 800 900
0
100
200
300
400
500
600
700
800
900
1000
n: Problem size−−−−−−−−>
CPUTime(seconds)−−−−−−−−−−−>
CPU Time Tradeoff of AHK Algorithm versus SeDuMi withε = 0.1 (Gaps)
m = 100 "AHK"
m = 200 "AHK"
m = 300 "AHK"
m = 100 "SeDuMi"
: Precision time tradeoff, CPU time taken by algorithm 1 and Se-
DuMi with respect to n (problem size)

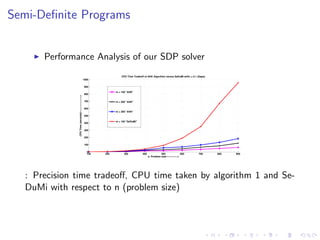
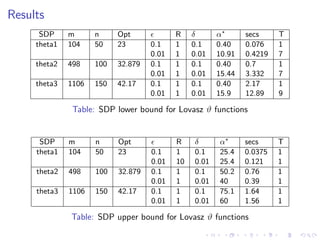
14. Example: Lovasz ϑ function
Consider following SDP problems from SDPLIB 1.2 [2]
theta1, theta2 and theta3
Given a graph G = (V , E), the lovasz ϑ-function ϑ(G) on G
is the optimal value of the following SDP
max J • X
I • X = 1
∀{i, j} ∈ E : Eij • X = 0
X 0.
Where
I is identity matrix
J is matrix in which every entry is 1
For each edge {i, j} ∈ E, Eij is the matrix in which both the
(i, j)-th and (j, i)-th entries are 1, and every other entry is 0

15. Example: Lovasz ϑ function
SDPLIB solves:
SDP
P : min A0 • X
subject to Aj • X = bj , j = 1, 2, ..., m
X 0
Relaxation of SDPLib SDPs:
min A0 • X
subject to Aj • X ≥ bj −
−Aj • X ≥ −bj − for j = 1, 2, ..., m and > 0
X 0
Tr(X) ≤ R.

16. Results
SDP m n Opt R δ α secs T
theta1 104 50 23 0.1 1 0.1 0.40 0.076 1
0.01 1 0.01 10.91 0.4219 7
theta2 498 100 32.879 0.1 1 0.1 0.40 0.7 1
0.01 1 0.01 15.44 3.332 7
theta3 1106 150 42.17 0.1 1 0.1 0.40 2.17 1
0.01 1 0.01 15.9 12.89 9
Table: SDP lower bound for Lovasz ϑ functions
SDP m n Opt R δ α secs T
theta1 104 50 23 0.1 1 0.1 25.4 0.0375 1
0.01 10 0.01 25.4 0.121 1
theta2 498 100 32.879 0.1 1 0.1 50.2 0.76 1
0.01 1 0.01 40 0.39 1
theta3 1106 150 42.17 0.1 1 0.1 75.1 1.64 1
0.01 1 0.01 60 1.56 1
Table: SDP upper bound for Lovasz ϑ functions

17. Conclusions
In every iteration interior point methods compute the
Cholesky decomposition of a PSD matrix. This computation
takes O(n3) time. The top eigenvector of a matrix can be
computed much more efficiently, which is done in algorithm 1.
This is where our implementation gets an edge over interior
point methods.
Second advantage of our implementation is that the Cholesky
decomposition of the final solution is calculated automatically
(X = T
t=1
Xt
T ).
We have presented our experimental results on solving relaxed
SDPs Lovasz ϑ functions and presented how we approach
towards the optimum one. Our results are good in quality and
efficient in compare to existing one.

18. Future Works
Presently our implementation runs sequentially, which may
not be good for considerable large combinatorial optimization
problems.
In future I am willing to implement approximation algorithms
in a distributed setup. This will give us faster results in
compare to existing one. Distributed setup implementation
will also have good quality of results as we have know.
There has been considerable recent research building on this
work, developing fast and parallel approximate algorithms to
approximate solutions to packing-covering linear as well as
semi-definite programs.
This research direction seem to be more interesting and can
have reasonable payoff and hence it can not be ignored.

19. S. Arora and S. Kale.K07
A combinatorial, primal-dual approach to semidefinite
programs.
In Proceedings of the Thirty-Ninth Annual ACM Symposium
on Theory of Computing, pages 227–236, 2007.
Brian Borchers.B99
Sdplib 1.2, a library of semidefinite programming test
problems.
11(1):683–690, 1999.
Rajiv Raman Dilys Thomas and Ajay Shankar Bidyarthy.A12
Fast approximations to solve packing-covering lps and
constant-sum games via multiplicative-weights technique.
In proceeding of the International Symposium on
Combinatorial Optimization - CO 2012, September 17-19
2012.
S. Arora E. Hazan and S. Kale.K05
Fast algorithms for approximate semidefinite programming
using the multiplicative weights update method.

20. In Proceedings of the 46th Annual IEEE Symposium on
Foundations of Computer Science, pages 339–348, 2005.
M.D. Grigoriadis and L.G. Khachiyan.K95
A sublinear-time randomized apprximation algorithm for
matrix games.
Operations Research Letters, 18(2):53–58, 1995.
Christos Koufogiannakis and Neal E. Young.Y07
Beating simplex for fractional packing and covering linear
programs.
The 48th IEEE Symposium on Foundation of Computer
Science, 2007.
Jos. F. Strum.uMi
Sedumi ver. 1.3.
Optimization Methods and Software.