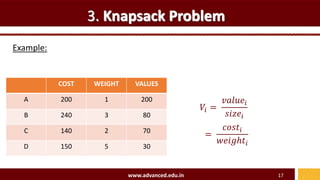
The document discusses greedy algorithms and the knapsack problem. It defines greedy algorithms as making locally optimal choices at each step to find a global optimum. The general method is described as starting with a small solution and building up, making short-sighted choices. Knapsack problems aim to fill a knapsack of size S with items of varying sizes and values, often choosing items with the highest value-to-size ratios first. The fractional knapsack problem allows items to be partially selected to maximize total value within the size limit.

1. Analysis & Design of
Algorithms
www.advanced.edu.in 1

2. Greedy Algorithms
Greedy Algorithms
The General Method
Continuous Knapsack Problem
www.advanced.edu.in 2

3. 1. Greedy Algorithms
Greedy Algorithm:
A greedy algorithm is an algorithm that follows the
problem solving heuristic of making the locally
optimal choice at each stage with the hope of finding
a global optimum.
www.advanced.edu.in 3

4. 1.Greedy Algorithms
Methodology:
 Start with a solution to a small sub-problem
 Build up to the whole problem
 Make choices that look good in the short term but
not necessarily in the long term
www.advanced.edu.in 4

5. 1.Greedy Algorithms
Advantages:
 When they work, they work fast
 Simple and easy to implement
Disadvantages:
 They do not always work.
 Short term choices may be disastrous on the long
term.
 Correctness is hard to prove
www.advanced.edu.in 5

6. 1.Greedy Algorithms
Applications:
 Applications of greedy method are very board
Example:
 Sorting.
 Merging sorted list.
 Knapsack
 Minimum Spanning Tree (MST)
 Hoffman Encoding
www.advanced.edu.in 6

7. 1.Greedy Algorithms
Characteristics and Features:
To construct the solution in an optimal way. Algorithm
maintains two sets. One contains chosen items and
the other contains rejected items.
The greedy algorithm consists of four (4) function.
A function that checks whether chosen set of items
provide a solution.
www.advanced.edu.in 7

8. 1.Greedy Algorithms (Cont.)
Characteristics and Features:
A function that checks the feasibility of a set.
The selection function tells which of the candidates is
the most promising.
An objective function, which does not appear
explicitly, gives the value of a solution.
www.advanced.edu.in 8

9. 2. The General Method
Let a[ ] be an array of elements that may contribute to
a solution. Let S be a solution,
Greedy (a[ ],n)
{
S = empty;
for each element (i) from a[ ], i = 1:n
{
x = Select (a,i);
if (Feasible(S,x)) S = Union(S,x);
}
return S;
}
www.advanced.edu.in 9

10. 2. The General Method (Cont.)
 Select:
Selects an element from a[ ] and removes it. Selection is optimized
to satisfy an objective function.
 Feasible:
True if selected value can be included in the solution vector, False
otherwise.
 Union:
Combines value with solution and updates objective function.
www.advanced.edu.in 10

11. 3. Knapsack Problem
There are two versions of the problem:
1. 0-1 Knapsack Problem
2. Fractional Knapsack Problem
i. Bounded Knapsack Problem
ii. Unbounded Knapsack Problem
www.advanced.edu.in 11

12. 3. Knapsack Problem
In a knapsack problem or rucksack problem,we are given a set of 𝑛items,
where each item 𝑖is specified by a size 𝑠𝑖 and a value 𝑣𝑖. We are also given
a size bound 𝑆, the size of our knapsack.
www.advanced.edu.in 12
Item i Size si Value vi
1 1 8
2 3 6
3 5 5

13. 3. Knapsack Problem
Environment:
Object (i):
Total Weight wi
Total Profit pi
Fraction of object (i) is continuous (0 =< xi <= 1)
A Number of Objects
1 =< i <= n
A knapsack
Capacity m
www.advanced.edu.in 13
Objects
1 2
3 n
Capacity
M

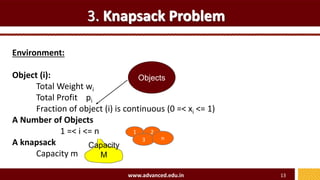
14. 3. Knapsack Problem
GreedyKnapsack ( p[ ] , w[ ] , m , n ,x[ ] )
{
insert indices (i) of items in a maximum heap on value vi = pi / wi ;
Zero the vector x; Rem = m ;
For k = 1..n
{ remove top of heap to get index (i);
if (w[i] > Rem) then break;
x[i] = 1.0 ; Rem = Rem – w[i] ;
}
if (k < = n ) x[i] = Rem / w[i] ;
}
// T(n) = O(n log n)
www.advanced.edu.in 14

15. 3. Knapsack Problem
Example:
www.advanced.edu.in 15
Given:
𝑛 = 4 (# of elements)
𝑆 = 5 pounds (maximum size)
Elements (size, value) =
{ (1, 200), (3, 240), (2, 140), (5, 150) }

16. 3. Knapsack Problem
Example:
www.advanced.edu.in 16
1. Calculate Vi =
vi
si
for 𝑖 = 1,2, … , 𝑛
2. Sort the items by decreasing Vi
3. Find j, such that
𝑠1 + 𝑠2 + ⋯ + 𝑠𝑗 ≤ 𝑆
< 𝑠1 + 𝑠2 + ⋯ + 𝑠𝑗+1

17. 3. Knapsack Problem
Example:
www.advanced.edu.in 17
𝑉𝑖 =
𝑣𝑎𝑙𝑢𝑒𝑖
𝑠𝑖𝑧𝑒𝑖
=
𝑐𝑜𝑠𝑡𝑖
𝑤𝑒𝑖𝑔ℎ𝑡𝑖
COST WEIGHT VALUES
A 200 1 200
B 240 3 80
C 140 2 70
D 150 5 30

18. 3. Knapsack Problem
Solution is:
www.advanced.edu.in 18
1 pounds A
3 pounds B
2 pounds C
4 pounds D

19. THANK YOU
www.advanced.edu.in 19
Contact Email Id: nikitaguptapalwal@gmail.com
Website: http://www.advanced.edu.in