Downloaded 99 times
Uploaded bySetu Chokshi
Time series predictions using LSTMs
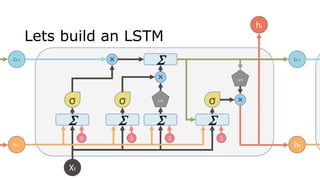
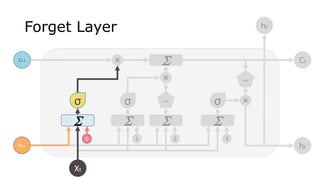
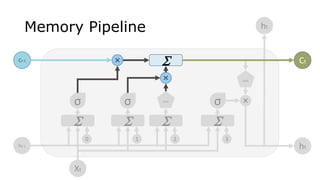
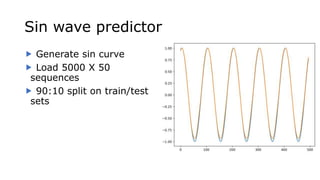
The document discusses the use of Long Short-Term Memory (LSTM) networks for time series predictions, detailing their architecture and functionality. It highlights methods to incorporate memory into neural networks to effectively model time series data and provides examples using sine wave prediction and power consumption datasets. Additionally, it includes several references for further understanding of LSTM networks and their application.
More Related Content
![[Infographic] How will Internet of Things (IoT) change the world as we know it?](https://cdn.slidesharecdn.com/ss_thumbnails/iotinfographicv3-160309101328-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Time series predictions using LSTMs
Time series predictions using LSTMs
- 1. Time Series Predictions usingLong Short-Term Memory Setu Chokshi IoT Asia 2017 – 30th March
- 2.
- 3. What are NeuralNetwork Y1 Y2 X1 X2 X3 h1 h2 h3 h4 Information Transfer Input Values Calculator – Activations Output (Activation) 1 2 3 4 Input Hidden Output X1 X2 X3 W11 W21 W31 h1 Example of = REctified Linear Unit = max(0,input) Strengthen weak signals; Leave strong signals alone Weight is the strength of the connection between nodes 1
- 4. Challenges Only fixedsized inputs & outputs Performs mapping of features from input to output No memory and hence difficult to model time series
- 5. Lets add somememory Input Hidden Output Input + prevInput Hidden Output Input+ prevHidden Hidden Output Input + prevInput Hidden Output Input + prevInput Hidden Output Input + prevInput Hidden Output Input + prevInput Hidden Output Input + prevHidden Hidden Output Input + prevHidden Hidden Output Input + prevHidden Hidden Output Input + prevHidden Hidden Output Approach 1: Add previous inputs Approach 2: Add previous hidden Lets do 4 time series steps Lets do 4 time series steps
- 6. Lets add somememory…and color Input Hidden Output Input + prevInput Hidden Output Input+ prevHidden Hidden Output Input + prevInput Hidden Output Input + prevInput Hidden Output Input + prevInput Hidden Output Input + prevInput Hidden Output Input + prevHidden Hidden Output Input + prevHidden Hidden Output Input + prevHidden Hidden Output Input + prevHidden Hidden Output Approach 1: Add previous inputs Approach 2: Add previous hidden Lets do 4 time series steps Lets do 4 time series steps
- 7. Lets build anLSTM Xt 0 1 2 3 ht-1 Ct-1 Ct✖ ✖ ✖σ σ σtanh tanh ht ht Ct-1
- 8. Now lets buildan LSTM Element- wise Summation / Concatenati on Element- wise multiplicatio n X t ht- 1 Ct- 1 h t C t 0 σ ✖ tanh Inputs: Outputs: Input vector Memory from previous blockOutput of previous block Memory from current blockOutput of current block Nonlinearities: Sigmoid Hyperbolic tangent Vector operations: Bias:
- 9. Lets skip themath, ok? Element- wise summation Element- wise multiplicatio n ✖ = =
- 10. Memory Pipeline Xt 0 1 2 3 ht-1 Ct-1 C t ht ✖ ✖ ✖σ σ σtanh tanh ht ✖
- 11. Forget Layer Xt 0 1 2 3 ht-1 Ct-1 Ct ht ✖ ✖ ✖σ σ σtanh tanh ht
- 12. Generate new memories:Input Xt + 0 1 2 3 ht-1 Ct-1 Ct ht ✖ ✖ ✖σ σ σtanh tanh ht 2 tanh
- 13. Generate new memories:Candidate Xt 0 1 2 3 ht-1 Ct-1 Ct ht ✖ ✖ ✖σ σ σtanh tanh ht
- 14. Memory Pipeline Xt 0 1 2 3 ht-1 Ct-1 Ct ht ✖ ✖ ✖σ σ σtanh tanh ht
- 15. Generate the output Xt 0 1 2 3 ht-1 Ct-1 Ct ht ✖ ✖ ✖σ σ σtanh tanh ht
- 16.
- 17. Sin wave predictor Generate sin curve Load 5000 X 50 sequences 90:10 split on train/test sets
- 18. Power Consumption Dataset Power Consumption Dataset 47 Months of data 2075259 measurements Active energy consumed per min Load 4567 X 50 sequences 90:10 split on train/test sets
- 19. References Understanding LSTMNetworks http://colah.github.io/posts/2015-08-Understanding- LSTMs/ General Sequence Learning using Recurrent Neural Networks https://www.youtube.com/watch?v=VINCQghQRuM Recurrent Neural Networks Part 1: Theory https://www.slideshare.net/gakhov Facebook Prophet https://github.com/facebookincubator/prophet Images adapted from Shi Yan https://medium.com/@shiyan/understanding-lstm-and-its- diagrams-37e2f46f1714 Anyone Can Learn To Code https://iamtrask.github.io/2015/11/15/anyone-can-code-lstm/
- 20.
Editor's Notes
- #4 Unlike all hidden layers in a neural network, the output layer units most commonly have as activation function: 1. Linear identity function (for regression problems) 2. Softmax (for classification problems).
- #11 If you multiply the old memory C_t-1 with a vector that is close to 0, that means you want to forget most of the old memory. You let the old memory goes through, if your forget valve equals 1. Then the second operation the memory flow will go through is this + operator. New memory and the old memory will merge by this operation. How much new memory should be added to the old memory is controlled by another valve, the ✖ below the + sign.
- #12 Sometimes it’s good to forget. If you’re analyzing a text corpus and come to the end of a document you may have no reason to believe that the next document has any relationship to it whatsoever, and therefore the memory cell should be reset before the network gets the first element of the next document. In many cases by reset we don’t only mean immediate set it to 0, but also gradual resets corresponding to slowly fading cell states