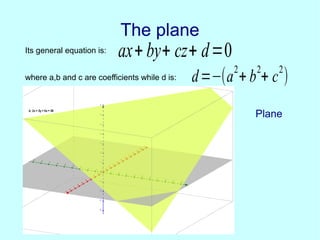
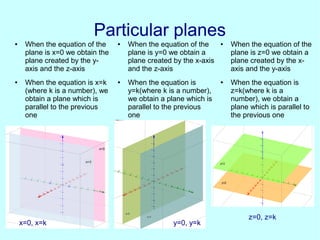
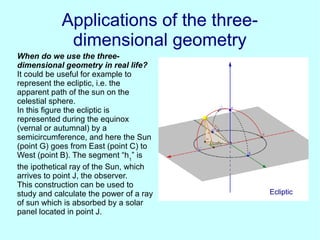
This document discusses analytic geometry in three dimensions. It begins by explaining the Cartesian coordinate system in three dimensions, using three axes (x, y, z) to locate a point in space. It then discusses how to calculate the distance and midpoint between two points. Next, it covers planes and their general and particular equations. It also discusses properties of planes like parallelism and perpendicularity. The document continues by defining straight lines and spheres, and provides their equations. It concludes by showing an example of a plane tangent to a sphere and discusses applications of three-dimensional geometry like representing the ecliptic.

1. ANALYTHIC GEOMETRYANALYTHIC GEOMETRY
OFOF
THREE DIMENSIONSTHREE DIMENSIONS
Corradi Davide, Codibue Martina 5^D liceo scientifico a.s. 2015/2016

2. Carthesian coordinate systemCarthesian coordinate system
● In a plane the point is originated by
two coordinates: “x” which is
associated with the x-axis, an
horizontal line with the positive
direction to the right, and “y”, which
is associated with the y-axis, i.e. a
vertical line with the positive
direction upward.
● The situation is different when we
consider the position of a point in
space: in fact we have to consider
three planes and, as a
consequence, three different axes
(x, y, z) and coordinates.
Representation of a point

3. The distance between two pointsThe distance between two points
and the segmentand the segment
● If we consider two different
points located in two different
positions on the three-
dimensional space, the
connection between them is
defined “segment”.
● The coordinates of the two
points are for example:
A(xA
,yA
,zA
) and B(xB
,yB
,zB
)
From these informations we can
calculate:
-the lenght of the segment AB:
-its midpoint:
AB=√((xA−xB)2
+( yA−yB)2
+ (zA−zB)2
)
xM=
(xA+ xB)
2
; yM=
(yA+ yB)
2
;zM=
(zA+ zB)
2
Segment

4. The planeThe plane
ax+ by+ cz+ d=0Its general equation is:
where a,b and c are coefficients while d is: d=−(a
2
+ b
2
+ c
2
)
Plane

5. Particular planesParticular planes
● When the equation of the
plane is x=0 we obtain the
plane created by the y-
axis and the z-axis
● When the equation is x=k
(where k is a number), we
obtain a plane which is
parallel to the previous
one
● When the equation of the
plane is y=0 we obtain a
plane created by the x-axis
and the z-axis
● When the equation is
y=k(where k is a number),
we obtain a plane which is
parallel to the previous
one
● When the equation of the
plane is z=0 we obtain a
plane created by the x-
axis and the y-axis
● When the equation is
z=k(where k is a
number), we obtain a
plane which is parallel to
the previous one
x=0, x=k y=0, y=k
z=0, z=k

6. Other informations about planesOther informations about planes
● The explicit equation of a plane
where:
m= -a/c
n= -b/c
q= (a
2
+ b
2
+ c
2
)
c
● Condition of parallelism between
planes:
plane one: ax+by+cz+d=0
plane two: a'x+b'y+c'z+d'=0
(
a
a
' )=(
b
b
')=(
c
c
')
z=mx+ ny+ q
● Condition of perpendicularity
between planes:
plane one: ax+by+cz+d=0
plane two: a'x+b'y+c'z+d'=0
● Distance between a point and a
plane:
(aa')+ (bb')+(cc')=0 h=
∣axA+ byA+ czA+ d∣
√a
2
+ b
2
+ c
2

7. The straight lineThe straight line
● A straight line is made of infinite points which derive from the intersection of
two different and non parallel planes.
Its general equation can therefore be written as a system of linear equations:
{ ax+ by+ cz+ d =0
a ' x+ b' y+ c' z+ d '=0
● When we have two different
points which belong to the
straight line we can use another
method to find its equation:
( x−x1)
(x2−x1)
=
( y− y1)
( y2− y1)
=
(z−z1)
(z2−z1)
↓
{
(x−x1)
(x2−x1)
=
( y− y1)
( y2− y1)
( y− y1)
( y2−y1)
=
(z−z1)
(z2−z1) Straight line

8. Definition of surfaces andDefinition of surfaces and
the spheric surfacethe spheric surface
● In the three-dimensional space a surface is defined as a set of points called
locus whose location satisfies or is determined by one or more particular
conditions.
For example these conditions can be an algebric equation.
● The spheric surface is defined as a locus whose property is that all its
points have the same distance called radius(r) from its center.
Coordinates of the center: C(x0
;y0
;z0
)
Ipothetical point of the sphere: P(x;y;z)
calculating their distance we obtain the equation of the sphere:
↓
(x−x0)
2
+(y−y0)
2
+ (z−z0)
2
=r
2
→ x
2
+ y
2
+ z
2
+ ax+ by+ cz+ d=0

9. Spheric surface

10. Composition of figuresComposition of figures
● In this picture we can see a composition of two figures in the three-
dimensional space: a spheric surface and a plane.
The peculiarity of this composition is that the plane is tangent to the surface
of the sphere, i.e. the two figures shares only one point.
Plane tangent to a spheric surface

11. Applications of the three-Applications of the three-
dimensional geometrydimensional geometry
When do we use the three-
dimensional geometry in real life?
It could be useful for example to
represent the ecliptic, i.e. the
apparent path of the sun on the
celestial sphere.
In this figure the ecliptic is
represented during the equinox
(vernal or autumnal) by a
semicircumference, and here the Sun
(point G) goes from East (point C) to
West (point B). The segment “h1
” is
the ipothetical ray of the Sun, which
arrives to point J, the observer.
This construction can be used to
study and calculate the power of a ray
of sun which is absorbed by a solar
panel located in point J.
Ecliptic