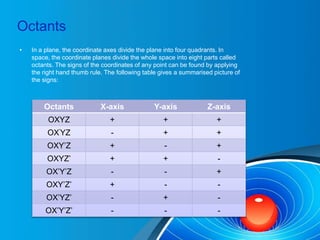
This document discusses coordinates in space and three-dimensional coordinate geometry. It introduces points, lines, and planes in three-dimensional space and how they are represented using ordered triples of real numbers called coordinates. It describes how the three mutually perpendicular coordinate axes divide space into eight octants. It provides formulas for finding distances between points, section formulas, midpoints, and centroids. It also discusses direction cosines and direction ratios as ways to represent the direction of lines in space, and provides formulas for finding angles between lines based on their direction cosines or direction ratios.

1. Coordinates in space
Class 12 Maths

2. Introduction
• Space is a term we use to describe the presence of material objects in
relation to one another or their movements. In other words, the notion of
space is closely associated with material objects in relative rest and/or
motion. We consider a point as an idealized model of a small material
object or particle. When we combine small material objects or particles
together, they form bigger objects. Similarly, when we combine points
together, they give rise to various forms or shapes. A systematic study
of such sets of points or shapes can be done by associating each of
such points with an ordered set of real numbers. Such numbers are said
to be coordinates of a given point on the space under consideration.

3. Coordinates in Space
• The study of coordinate geometry begins by establishing a one-to-
one correspondence between the points on a line and the real
numbers. For this, we associate each point in a plane with an
ordered pair of real numbers. Each point in the ordinary space (or
three dimensional space) can be associated with an ordered triple
of real numbers.
• To start with, we consider three mutually perpendicular lines
intersecting at a fixed point. This fixed point is called origin and the
three lines are called coordinate axes. The coordinate axes are
labelled as the x-axis, the y-axis and the z-axis.

4. Octants
• In a plane, the coordinate axes divide the plane into four quadrants. In
space, the coordinate planes divide the whole space into eight parts called
octants. The signs of the coordinates of any point can be found by applying
the right hand thumb rule. The following table gives a summarised picture of
the signs:
Octants X-axis Y-axis Z-axis
OXYZ + + +
OX’YZ - + +
OXY’Z + - +
OXYZ’ + + -
OX’Y’Z - - +
OXY’Z’ + - -
OX’YZ’ - + -
OX’Y’Z’ - - -

5. Distance formula
• In three-dimensional Cartesian space, points have three
coordinates each. To find the distance between A(x1,y1,z1) and
B(x2,y2,z2)we have,
• D= 𝑥2 − 𝑥1
2 + 𝑦2 − 𝑦1
2 + 𝑧2 − 𝑧1
2
Section formula
• The formula that gives the points of division are called section
formulae
• LetA(x1,y1,z1)and B(x2,y2,z2)are the two points in3 – dimensional
space. C (x, y, z) divides the line joining A and B in the ratio m:n
• a. Internally
• Coordinates of C=
𝑚𝑥2+𝑛𝑥1
𝑚+𝑛
,
𝑚𝑦2+𝑛𝑦1
𝑚+𝑛
,
𝑚𝑧2+𝑛𝑧1
𝑚+𝑛
• b. Externally
• Coordinates of C=
𝑚𝑥2−𝑛𝑥1
𝑚−𝑛
,
𝑚𝑦2−𝑛𝑦1
𝑚−𝑛
,
𝑚𝑧2−𝑛𝑧1
𝑚−𝑛

6. Mid-point
• Co-ordinates of the middle point of the line segment joining
A(x1,y1,z1)and B(x2,y2,z2) are:
• R=
𝑥1+𝑥2
2
,
𝑦1+𝑦2
2
,
𝑧1+𝑧2
2
Centroid of a Triangle
• Co-ordinates of the centroid of a triangle having vertices
A(x1,y1,z1), B(x2,y2,z2) and C(x3,y3,z3) are:
• R=
𝑥1+𝑥2+𝑥3
2
,
𝑦1+𝑦2+𝑦3
2
,
𝑧1+𝑧2+𝑧3
2

7. DIRECTION COSINES AND
DIRECTION RATIOS

8. Angle between Two lines
• Any wo lines in a plane are either parallel or intersected. However in space,
there may be two lines which are neither parallel nor intersecting and may
not be in same plane. These lines are called skew lines.
• The angle between the skew lines is the angle between two lines drawn
parallel to the given lines through any point in space.
• In three-dimensional space, the angle between two lines can be determined
similarly to the angle between two lines in a coordinate plane. If the two lines
have these equations: r=a1+λb1 and r=a2+λb2, then the following formula is
given for the angle between two lines:
• cos𝜃=b1.b2/ |b1|.|b2|
• In a 3D space, straight lines are usually represented in two ways: cartesian
form or vector form. As a result, the angles formed by any two straight lines
in the 3D space are specified in terms of both their forms.
A C
B
R
S
P Q

9. Direction Cosines of a Line
• Let 𝛼, 𝛽, 𝛾 be the angles which a directed line makes with positive x-axis, y-
axis and z-axis respectively. These angles are called direction angles of the
line. More precisely, the direction angles of the directed line OP in the given
figure.
• 𝛼=∠BOP=Angle between OP and positive x-axis
• 𝛽=∠AOP=Angle between OP and positive y-axis
• 𝛾=∠COP=Angle between OP and positive z-axis
• The cosines of the above angles of the straight line OP are called direction
cosines of the line OP. They are usually denoted by l,m,n. Therefore l=cos𝛼,
m=cos𝛽 and n=cos𝛾.

10. ✔Direction cosines of X-axis are 1,0,0 , Y-axis
are 0,1,0 and Z-axis are 0,0,1
✔If the direction cosines of AB are l=cos𝛼,
m=cos𝛽 and n=cos𝛾 then direction cosines
of BA is l=-cos𝛼, m=-cos𝛽 and n=-cos𝛾.

11. Relation among Direction Cosines of a line
Let 𝛼, 𝛽, 𝛾 be the angle made by a line AB with OX, OY and OZ respectively so
that cos𝛼, cos𝛽 and cos𝛾 are the direction cosines of AB.
i.e. l=cos𝛼, m=cos𝛽 and n=cos𝛾.
Let P be the point having coordinates (x, y, z) and OP = r
Then OP2 = x² + y² + z² = r² …. (1)
From P draw PA, PB, PC perpendicular on the coordinate axes, so that OA = x, OB = y,
OC = z.
Also, ∠POA = α, ∠POB = β and ∠POC = γ.
From triangle AOP, l = cos α = x/r ⇒ x = lr
Similarly y = mr and z = nr
From equation 1
r² (l² + m² + n²) = x² + y² + z² = r²
⇒ l² + m² + n² = 1

12. Direction Ratio of a Line
• The quantities that are proportional to the direction cosines,
are said to be direction ratios i.e. the three non-zero
numbers a, b, c are said to be direction ratios of a line with
the direction cosines l, m, n. If a, b, c are proportional to the
l, m, n.
• i.e.
𝑙
𝑎
=
𝑚
𝑏
=
𝑛
𝑐
=±
𝑙2+𝑚2+𝑛2
𝑎2+𝑏2+𝑐2
=±
1
𝑎2+𝑏2+𝑐2
• This implies that
• l =±
𝑎
𝑎2+𝑏2+𝑐2
, m =±
𝑏
𝑎2+𝑏2+𝑐2
, n =±
𝑐
𝑎2+𝑏2+𝑐2

13. Diection Cosines of a Line Through Two Points
Let a straight line PQ (=r) passing through the two given
points P(x1,y1,z1) and Q(x2,y2,z2). Draw PC⊥ z-axis. From C,
draw CD equal and parallel to PQ so that CD and PQ will be inclined
to the z-axis at the same angle γ (say). Now, draw DC′⊥ z-axis.
Then, we have
n=cosγ=
CC′
CD
∴n=cosγ=
𝑧2−𝑧1
𝑟
Similarly, we can find that
l=cosα=
𝑥2−𝑥1
𝑟
m=cosβ=
𝑦2−𝑦1
𝑟
Hence, direction cosines of PQ are
𝑥2−𝑥1
𝑟
,
𝑦2−𝑦1
𝑟
,
𝑧2−𝑧1
𝑟
Also,
𝑥2−𝑥1
cosα
=
𝑦2−𝑦1
cosβ
=
𝑧2−𝑧1
cosγ
=r where,
r= 𝑥2 − 𝑥1
2 + 𝑦2 − 𝑦1
2 + 𝑧2 − 𝑧1
2
•

14. Angle Between two lines whose direction
cosines are given

15. • Expression for sin𝜽
• sin𝜃=
𝑙1𝑚2 − 𝑙2𝑚1
2 + 𝑚1𝑛2 − 𝑚2𝑛1
2 + 𝑛1𝑙2 − 𝑛2𝑙1
2
• Condition of perpendicularity of two lines:
• 𝑙1𝑙2 + 𝑚1𝑚2 + 𝑛1𝑛2 = 0
• Condition of parallelism of two lines:
•
𝑙1
𝑙2
=
𝑚1
𝑚2
=
𝑛1
𝑛2

16. • Angle between two lines with given direction
ratio:
• cos𝜃= ±
𝑎1𝑎2+𝑏1𝑏2+𝑐1𝑐2
𝑎1
2+𝑏1
2
+𝑐1
2 𝑎2
2+𝑏2
2
+𝑐2
2
• Condition for perpendicularity:
• 𝑎1𝑎2 + 𝑏1𝑏2 + 𝑐1𝑐2=0
• Condition for parallelism:
•
𝑎1
𝑎2
=
𝑏1
𝑏2
=
𝑐1
𝑐2