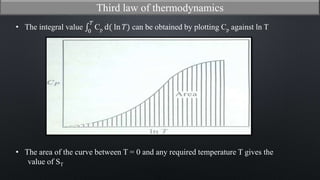
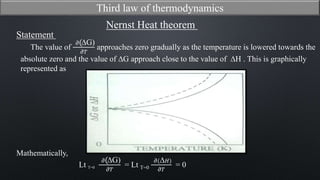
This document discusses the third law of thermodynamics. It states that the entropy of a perfectly crystalline substance is zero at absolute zero temperature. The mathematical expressions for determining absolute entropy are provided. The document also discusses Nernst's heat theorem, which states that the change in Gibbs free energy of a reaction approaches the change in enthalpy as temperature approaches absolute zero. Exceptions to the third law for certain gases with non-ordered crystal structures are also noted.

1. THERMODYNAMICS - III
Dr.P.GOVINDARAJ
Associate Professor & Head , Department of Chemistry
SAIVA BHANU KSHATRIYA COLLEGE
ARUPPUKOTTAI - 626101
Virudhunagar District, Tamil Nadu, India

2. Third law of thermodynamics
Determination of absolute entropy
• At constant pressure equation (1) becomes
dS =
𝑑𝑞
𝑇
-------(1)
(𝜕S)p =
𝜕𝑞 𝑝
𝑇
-------(2)
𝜕𝑆
𝜕𝑇 p =
𝜕𝑞
𝜕𝑇 p x
1
𝑇
--------(3)
At the absolute zero of temperature, the entropy of every substance may become
zero and it does become zero in the case of a perfectly crystalline structure.
Statement
• The mathematical expression for change in entropy is
• Divide on both side of equation (2) by dT

3. dS = Cp x
𝑑𝑇
𝑇
-------(5)
0
𝑆 𝑇
𝑑𝑆 = 0
𝑇
Cp
𝑑𝑇
𝑇
-------(6)
ST = 0
𝑇
Cp d( ln 𝑇) -------(7)
Where ST is the absolute entropy
Third law of thermodynamics
𝜕𝑆
𝜕𝑇 p = Cp x
1
𝑇
-------(4)
• Since
𝜕𝑞
𝜕𝑇 P is equal to Cp , the equation (3) becomes
• Integrate equation (5) within the limits
• Since d( ln 𝑇) is equal to
𝑑𝑇
𝑇
, the equation (6) becomes

4. Third law of thermodynamics
• The area of the curve between T = 0 and any required temperature T gives the
value of ST
• The integral value 0
𝑇
Cp d( ln 𝑇) can be obtained by plotting Cp against ln T

5. Exceptions of Third law
According to third law of thermodynamics the entropy of the crystalline
solid is zero at 0 K. But for some gases like CO, NO and N2O, the entropies
of their crystalline solid state are not zero at 0 K
Explanation
• These gases are having two alternative arrangements of molecule in
their crystal lattices structure as shown as
CO and OC
NO and ON
NNO and ONN
• So that the crystals of these gases does not have ordered structure (or)
perfect structure. It means that the entropies of the crystalline solids of
these gases might not be zero at 0 K
Third law of thermodynamics

6. Third law of thermodynamics
Statement
The value of
𝜕(∆G)
𝜕𝑇
approaches zero gradually as the temperature is lowered towards the
absolute zero and the value of ∆G approach close to the value of ∆H . This is graphically
represented as
Nernst Heat theorem
Mathematically,
Lt T=0
𝜕(∆G)
𝜕𝑇
= Lt T=0
𝜕(∆ 𝐻)
𝜕𝑇
= 0

7. Third law of thermodynamics
• Gibbs Helmholtz equation is
∆G = ∆ H + T
𝜕(∆G)
𝜕𝑇 P
∆G - ∆H = T
𝜕(∆G)
𝜕𝑇 P -------(1)
• At absolute zero temperature i.e., (T = 0 K), equation (1) becomes
∆G - ∆ H = 0
∆G = ∆ H
Explanation
∆G - ∆H = 0 x
𝜕(∆G)
𝜕𝑇 P

8. Significance of Nernst heat theorem
𝜕(∆G)
𝜕𝑇 P = - ∆S --------(1)
𝜕(∆ 𝐻)
𝜕𝑇 P = ∆Cp --------(2)
• Where
∆S is the change of entropy for a reaction
∆Cp is the difference in the heat capacities of the product and reactant
Third law of thermodynamics
• From second law of thermodynamics, ∆S and ∆Cp for the reaction is expressed as
• For a chemical reaction
Reactant Product

9. • According to Nernst heat theorem
Lt T = 0
𝜕(∆G)
𝜕𝑇 P
= Lt T = 0 ∆S = 0
Lt T = 0
𝜕(∆ 𝐻)
𝜕𝑇 P
= Lt T = 0 ∆Cp = 0
• i.e., Lt T = 0 ∆S = 0
Lt T = 0 ∆Cp = 0
• i.e., the entropy change of a reaction tends to approach zero and that the
difference between the heat capacities of product and reactant tends to approach
zero as the temperature is lowered towards the absolute zero
Third law of thermodynamics

10. THANK YOU