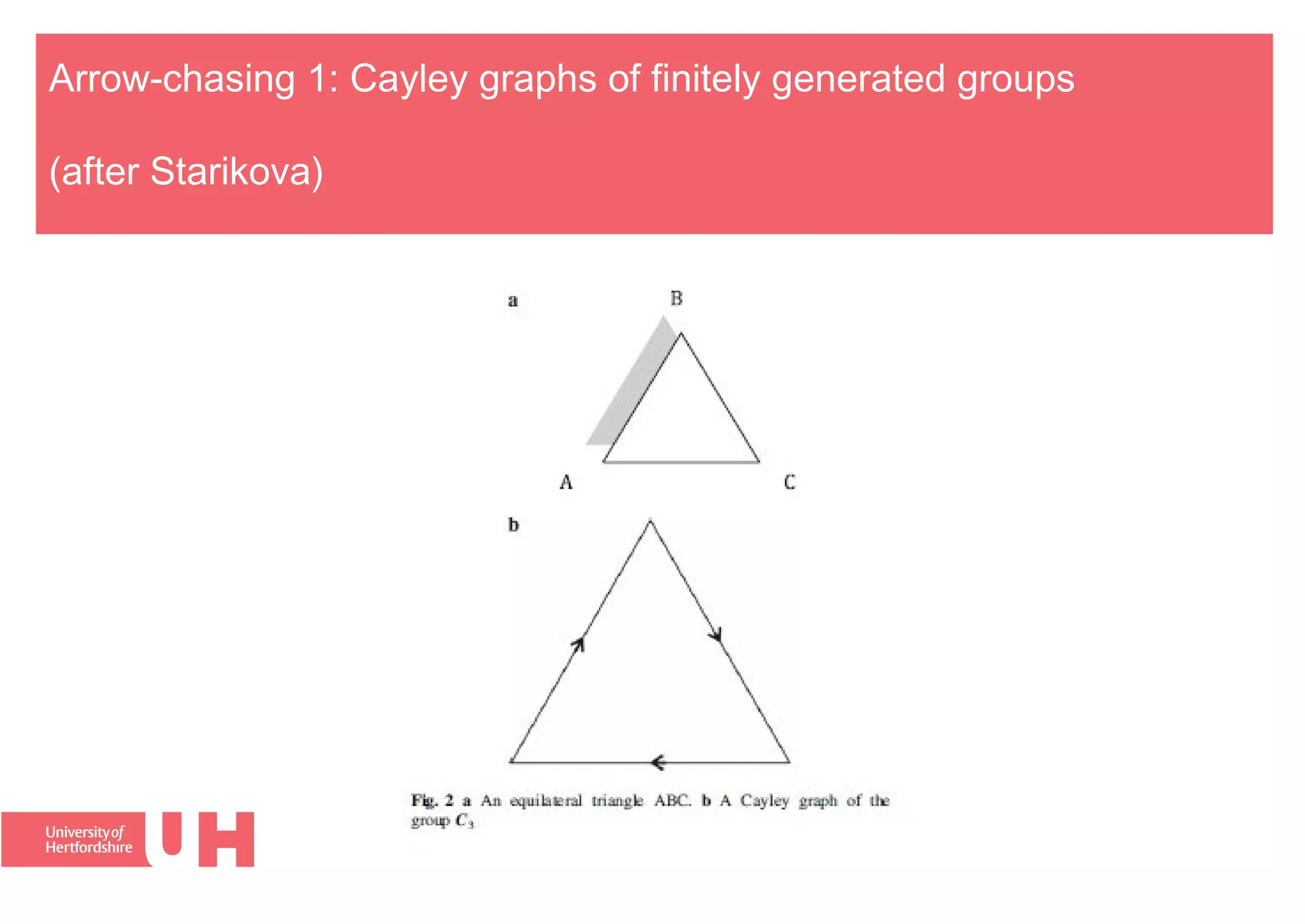
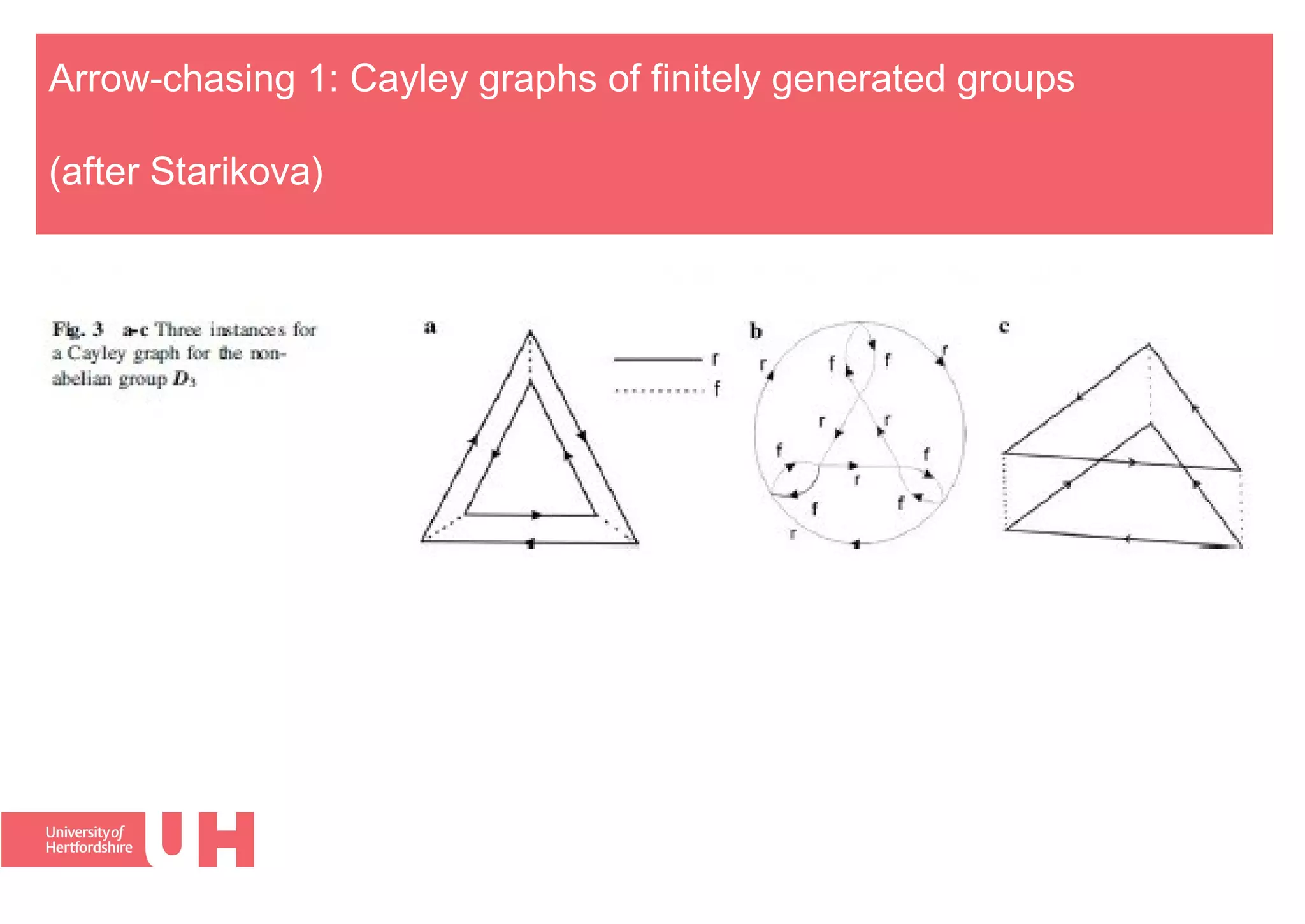
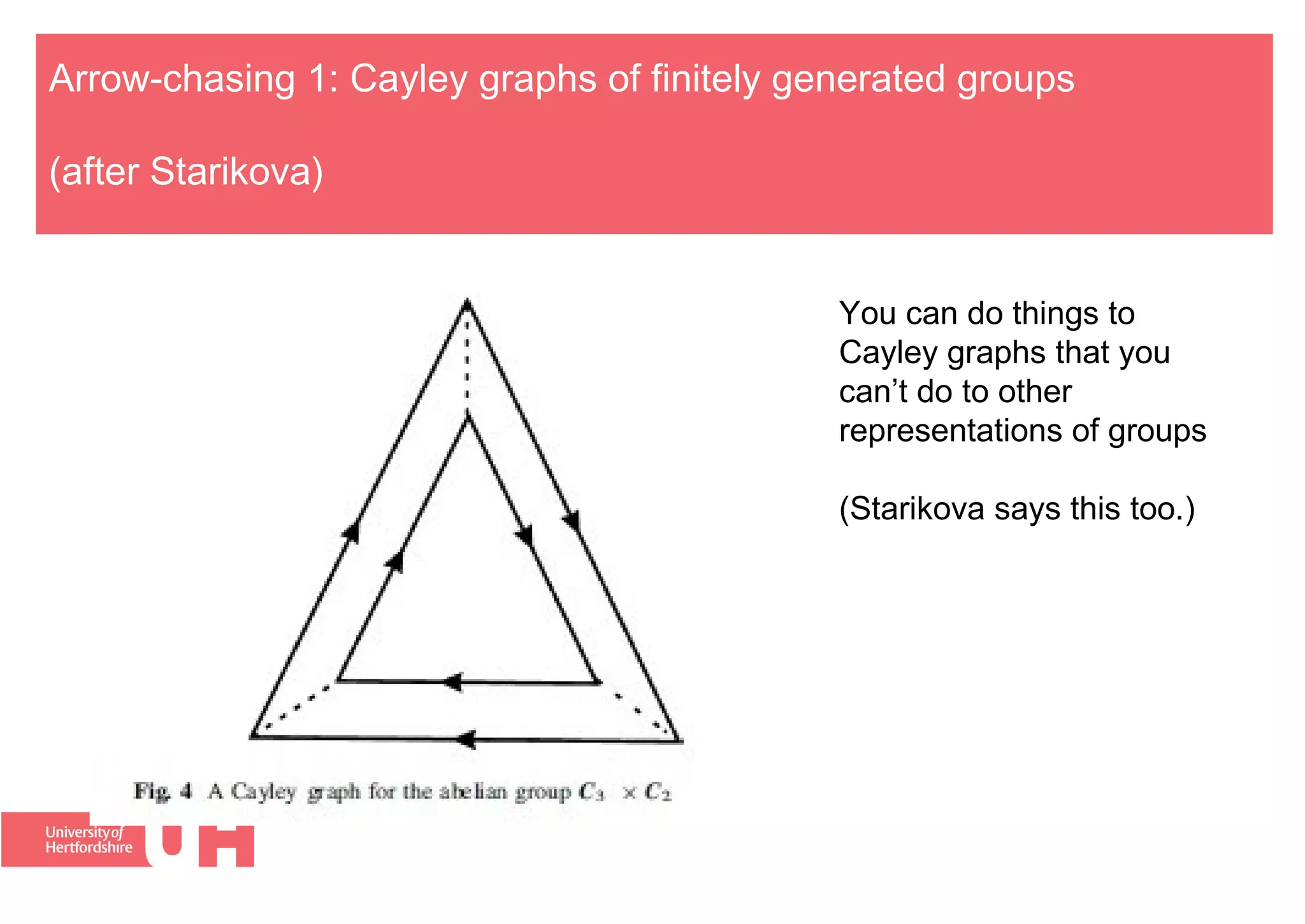
The document discusses the logic of informal proofs in mathematics. It makes 5 key claims: 1) Understanding informal proofs is important because most mathematical proofs are informal. 2) Informal proofs rely on both logical form and content. 3) Properly understanding informal proofs requires seeing logic as the study of inferential actions, where content plays a role. 4) This conception accommodates proofs involving actions on objects other than propositions. 5) It explains why mathematics relies on external representations, since representations can be manipulated. The document argues this view connects logical questions about rigor to the cultural study of mathematical practices.

1. 9 June 2014
The Logic Of Informal Proofs
Oxford University Philosophy of Mathematics Seminar

2. The Claims:
1. progress in the philosophy of mathematical practice requires a general positive account of
informal proof (since almost all mathematical proofs are informal in the strictest sense,
even if they are highly formalised);
2. informal proofs are arguments that depend on their matter as well as their logical form (in
other words, ‘informal’ is a poor English translation for inhaltliche);
3. articulating the dependency of informal inferences on their content requires a reconception
of logic as the general study of inferential actions (in informal proofs, content, or
representations thereof, plays a role in inference as the object of such actions);
4. it is a decisive advantage of this conception of logic that it accommodates the many
mathematical proofs that include actions on objects other than propositions;
5. further, it explains the fact that mathematics is (aside from some elementary mental
arithmetic and simple spatial arguments) essentially inscribed.

3. As if that were not enough:
…this conception of logic facilitates an intimate connection between logical questions about
rigour and the study of mathematical cultures and practices (since the logical constraints on
inferential actions are enacted as cultural norms).
This is what we need, because at the moment, in the philosophy of mathematical practice,
we have on the one hand a stock complaint about formal logic as an explanatory model of
mathematical proof, and on the other an increasingly rich literature of studies of specific
mathematical practices. The model I present can draw on the latter to supply the deficiency
identified by the former.

4. 1: progress in the philosophy of mathematical practice requires a
general positive account of informal proof (since almost all
mathematical proofs are informal in the strictest sense, even if they
are highly formalised);
The case against formal proofs as an account of how mathematical knowledge is validated
is staple at PMP conferences:
• There are very few fully formalised proofs;
• Fully formalised proofs of significant theorems would be impossibly huge (bigger
than the solar system)
• On the ‘formalist’ view, a regular proof is an informal argument that a formal
derivation is possible—which is a mathematical claim. So we agree that regular
proofs are informal mathematical arguments. The disagreement is only about the
conclusion.
• Explaining mathematical agreement by reference to non-existent derivations
seems like magical thinking

5. 2: informal proofs are arguments that depend on their matter as well
as their logical form (in other words, ‘informal’ is a poor English
translation for inhaltliche);
Inhalt = content
Syllogisms are formal, even though they use no notation
There are defeasible and ampliative formal arguments (e.g. statistical
reasoning)
Most of the arguments people make in earnest depend for their inferences
on their content as well as their form (which is why the ‘fallacies’ of
argument-analysis are not always fallacious)

6. 3: articulating the dependency of informal inferences on their content
requires a reconception of logic as the general study of inferential
actions (in informal proofs, content, or representations thereof, plays a
role in inference as the object of such actions)
);This is not so radical:
• Formal logic offers a huge range of systems
• Formal logic has been extended to all manner of matters (tense logic, deontic logic, modal
logic, etc.)
• Consider arguments about moving furniture, or the possibility of a new gymnastic feat
• Philosophy of experimental science—the experiment is no longer simply a source of
protocol sentences. It is a locus of rational action.
• Mathematical proofs (or rather, their texts) are full of imperatives. The objects of these
imperatives are often not propositions but rather mathematical items or representations
thereof
• These actions are often only available in certain domains (co-set counting; divisibility
arguments; ε-δ chasing; Euclidean diagram manipulation;…)

7. 4: it is a decisive advantage of this conception of logic that it
accommodates the many mathematical proofs that include actions on
objects other than propositions;
);This is not so radical:
• Formal logic offers a huge range of systems
• Formal logic has been extended to all manner of matters (tense logic, deontic logic, modal
logic, etc.)
• Consider arguments about moving furniture, or the possibility of a new gymnastic feat
• Philosophy of experimental science—the experiment is no longer simply a source of
protocol sentences. It is a locus of rational action.
• Mathematical proofs (or rather, their texts) are full of imperatives. The objects of these
imperatives are often not propositions but rather mathematical items or representations
thereof
• These actions are often only available in certain domains (co-set counting; divisibility
arguments; ε-δ chasing; Euclidean diagram manipulation;…)

8. A ‘Cartesian’ Proof:

9. 5: further, it explains the fact that mathematics is (aside from some
elementary mental arithmetic and simple spatial arguments)
essentially inscribed.
);
The real value of mathematical representations is not that they present information clearly
(though they do) but that they offer themselves for manipulation.
Peirce: Icons
(thanks to Emily Grosholz)
Example from Polya:

10. Arrow-chasing 1: Cayley graphs of finitely generated groups
(after Starikova)

11. Arrow-chasing 1: Cayley graphs of finitely generated groups
(after Starikova)

12. Arrow-chasing 1: Cayley graphs of finitely generated groups
(after Starikova)
You can do things to
Cayley graphs that you
can’t do to other
representations of groups
(Starikova says this too.)

13. Arrow-chasing 2:

14. Arrow-chasing 2:

15. As if that were not enough:
…this conception of logic facilitates an intimate connection between logical questions about
rigour and the study of mathematical cultures and practices (since the logical constraints on
inferential actions are enacted as cultural norms).
E.g. thinking about Ken Manders’ analysis of Euclidean diagrams helps us to understand
Jessica Carter’s disappearing diagrams.
“At its most basic, a mathematical practice is a structure for cooperative effort in control of
self and life” (Manders p. 82; italics in original)
To use a new representation in a published proof, we have to do for it what Ken did for
Euclidean manipulations.

16. References
Awodey, Steve 2010 Category Theory (2nd
edition) Oxford
Grosholz, Emily R. 2007 Representation and Productive Ambiguity in Mathematics and the Sciences Oxford
Hacking, Ian 2014 Why Is There Philosophy of Mathematics At All? Cambridge
Lakatos, Imre 1976 Proofs and Refutations Cambridge: Cambridge University Press. John Worrall & Elie Zahar (eds)
Larvor, Brendan 2011 “How to think about informal proofs” Synthese pp. 1-16.
Larvor, Brendan 2012 “What Philosophy of Mathematical Practice Can Teach Argumentation Theory about Diagrams and Pictures”
The Argument of Mathematics Aberdein, A. & Dove, I. (eds.). Springer pp. 209-222.
Manders, Kenneth “Diagram-Based Geometric Practice” / “The Euclidean Diagram” (1995). . Chapter 3, pp. 65–79. / Chapter 4 in P.
Mancosu, ed., The Philosophy of Mathematical Practice. Oxford Univ Pr, 2008, pp. 80–133.
Netz, Reviel 1999 The Shaping of Deduction in Greek Mathematics: A Study in Cognitive History. Cambridge: Cambridge University Press,
Starikova, Irina 2010 “Why do Mathematicians Need Different Ways of Presenting Mathematical Objects? The Case of Cayley
Graphs” Topoi Volume 29, Issue 1 , pp 41-51