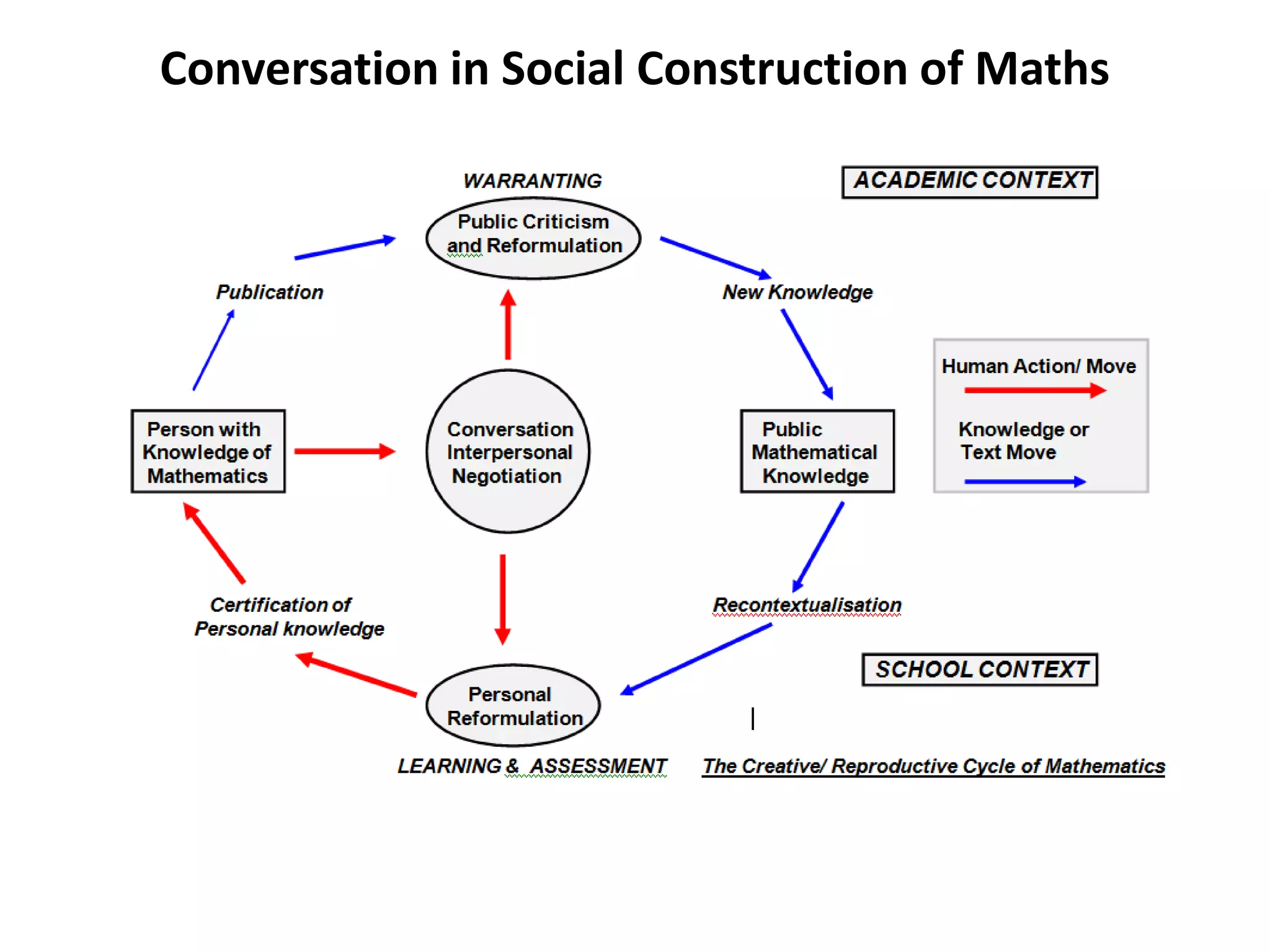
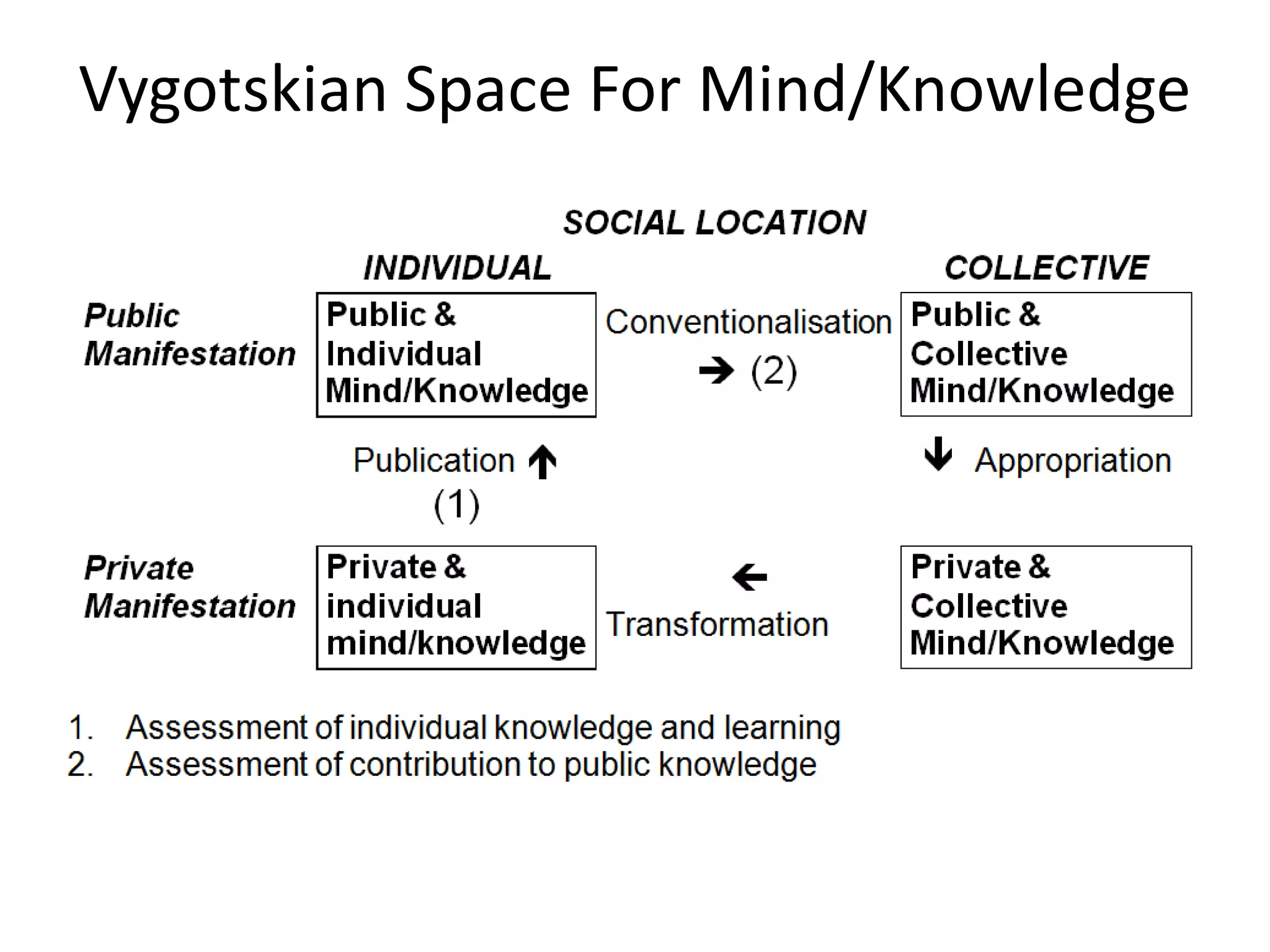
- Social constructivism views mathematical knowledge as a social and historical construct. It rejects the notion that mathematical knowledge is absolutely valid or certain. - Key aspects of social constructivism include viewing mathematical concepts and proofs as evolving through a conversational process of proposing ideas and subjecting them to criticism and refinement. Mathematical knowledge is seen as intersubjective rather than purely objective. - On this view, mathematical texts and concepts can be understood as participating in an ongoing conversation, with proponents putting forth ideas and critics examining them for weaknesses. The acceptance of mathematical ideas and proofs occurs through this social and dialogical process rather than being intrinsically certain.

1. SOCIAL CONSTRUCTIVISM AS A
PHILOSOPHY OF MATHEMATICS
Paul Ernest
University of Exeter, UK

2. SOCIAL CONSTRUCTIVISM AS A
PHILOSOPHY OF MATHEMATICS
THIS TALK IS BASED ON FOLLOWING
PUBLICATIONS
• Ernest, Paul (1998) Social Constructivism as a
Philosophy of Mathematics, Albany, New
York: SUNY Press.
• Ernest, P. (1991) The Philosophy of
Mathematics Education, London: Routledge.
(c) Paul Ernest 2015

3. MATHEMATICAL KNOWLEDGE NOT
ABSOLUTELY VALID
• 1. BASIS Proof in mathematics assumes (a) truth, or (b)
correctness, or (c) consistency of axioms and of logical rules. But
truth of this basis cannot be established without vicious circle.
• 2. PROOF Mathematical proof absolutely correct only if
unjustified assumptions made
• (a) Standards of absolute rigour attained. No grounds for assuming
this exist.
• (b) Any proof rigorizable. But virtually all accepted mathematical
proofs informal.
• (c) Check-ability of rigorous proofs for correctness is possible.
Further formalising informal proofs will lengthen them and make
checking even more uncertain.
• 3. SYSTEM Mathematical proof depends on the assumed safety
of axiomatic system. This unjustified after Gödel

4. Failure of Absolutism
• Absolute rigour unattainable. So claim of
absolute validity for mathematical knowledge
unjustified.
• Increasing recognition by philosophers that this is
so.
• Foundationist programmes of Formalism,
Logicism, Intuitionism each failed `to establish
maths knowledge as absolutely valid (cf. Russell,
Gödel)
• Growing agreement that any such absolutist or
foundationist enterprise must fail.

5. New Fallibilist Movement
• New 'maverick' tradition with Wittgenstein,
Davis, Hersh, Kitcher, Tymoczko, Lakatos
1. Rejects narrow philosophy of mathematics
focus on foundationist epistemology and
Platonistic ontology
2. Rejects exclusion of history and practice of
mathematics
3. Claims mathematical knowledge is fallible

6. What is fallibilism? 3 meanings
1. Fallibilism1: Humans make mistakes F1 is trivial. Clearly true.
2. Fallibilism2: (Some) mathematical knowledge is or may be
false (not F1) It is enough to find one falsehood or
contradiction and Gödel’s Theorem means we cannot
eliminate this possibility
But F2 assumes absolute truth judgements can be made.
Fallibilism3 denies this assumed absolutism
3. Fallibilism3: Maths is a relative, contingent, historical
construct
Absolute judgements re truth, correctness can never be
made. Criteria and definitions vary with time, context, never
final form.
This is a postmodern view of mathematics

7. Fallibilism3: Social Constructivism
• The concepts, definitions, rules of mathematics invented and evolved over
millennia, including rules of truth and proof.
• Fallibilism3 rejects Absolutism which assumes the following:
• Universalism: All knowing beings in all times & cultures would agree on
truth & mathematical knowledge.
• This is false if ‘do’ is put for ‘would’. But how could we ever know if this
were true? (An article of faith)
• Objectivism: Truth depends on objective reality, not views of
persons/groups
• This raises the problem of privileged access to ‘objective reality’, which
begs the question
• Foundationalism: There is a unique permanent foundation for
knowledge.
• This foundation has not been identified historically. Foundationalist
philosophies of mathematics (Logicism, Formalism, Intuitionism) all failed.

8. Wittgenstein’s Philosophy of Maths
• Wittgenstein’s naturalistic and fallibilist social philosophy of
maths based on key concepts of ‘language games’ - how we
use language coordinated with our actions - inseparably part
of ‘forms of life’ - our historico-cultural practices.
Mathematics teaches you, not just the answer to a question,
but a whole language-game with questions and answers.
The mathematician is not a discoverer: he is an inventor.
(Wittgenstein)
Proof serves to justify mathematical knowledge through
persuasion, not by its inherent logical necessity. W’s
philosophy fallibilist, because certainty grounded in accepted
(but always revisable) rules of language games (Rorty).

9. Lakatos’ Philosophy of Mathematics
• Lakatos contributed Logic of Mathematical Discovery
(LMD) or Method of Proofs and Refutations as
methodology of mathematics with 3 functions:
• Epistemology: To account for the genesis and
justification of mathematical knowledge naturalistically
as part of his Fallibilism3. (Present)
• Theory of historical development of mathematics -past
• Methodology for practising mathematicians (future)
• Lakatos' theory starts with a mathematical conjecture C
– an attempted proof of it - P and a background
informal theory T

10. Lakatos’ Logic of Math’l Discovery
STAGE CONTEXT PART OF CYCLE
Stage n1 Problem P, Informal
Theory T
Conjecture C
n2 - thesis Informal proof I of C
n3 - antithesis Informal refutation R of
C
Lakatos' LMD is a cyclic process with a dialectical form
Stage n has attempted proof I of C - generates a refutation R
of C. Next stage n+1 has new modified conjecture C’ (in
context of modified problem P’ and new informal theory T’)
(n+1)1 - synthesis Problem P’, Informal
Theory T’
Conjecture C’

11. Lakatos’ Fallibilism3
• The most radical aspect of Lakatos’ PM is his fallibilist
epistemology.
Why not honestly admit mathematical fallibility, and
try to defend the dignity of fallible knowledge from
cynical scepticism (Lakatos)
• Because:
1. Any attempt to find a perfectly secure basis leads to
infinite regress
2. Mathematical knowledge cannot be given a final,
fully rigorous form - “one so pay for each step which
increased rigour in deduction by the introduction of a
new and fallible translation.” (Lakatos)
• NB. Lakatos would not support Social Constructivism.
He believed mathematics is fallible3 but wholly rational
and not basically social

12. SC: Need to reconceptualise PM
• The philosophy of mathematics begins when
we ask for a general account of mathematics,
a synoptic vision of the discipline that reveals
its essential features and explains just how it is
that human beings are able to do
mathematics. (Tymoczko)
• The philosophy of mathematics should
account for more than just Mathematical
knowledge and the objects of mathematics

13. NEW CRITERIA NEEDED FOR PM
• An adequate philosophy of mathematics should account for all of:
• Epistemology: Mathematical knowledge; its character, genesis and
justification, with special attention to the role of proof
• Theories: Mathematical theories, both constructive and structural:
their character and development, and issues of appraisal and
evaluation
• Ontology: The objects of mathematics: their character, origins and
relationship with the language of mathematics, the issue of
Platonism
• Methodology and History: Mathematical practice: its character,
and the mathematical activities of mathematicians, in the present
and past
• Applications and Values: Applications of mathematics; its
relationship with science, technology, other areas of knowledge and
values
• Individual Knowledge and Learning: The learning of mathematics:
its character and role in the onward transmission of mathematical
knowledge, and in the creativity of individual mathematicians

14. Social Basis Of Social Constructivism
• (i) Based on Wittgenstein's notions of 'language game' and
'forms of life'. Mathematical knowledge rests on socially
situated linguistic practices, including shared rules,
meanings and conventions, i.e. on both tacit and explicit
knowledge and symbolic practices.
• (ii) Based on Lakatos' Logic of Mathematical Discovery for
negotiation and acceptance of mathematical knowledge,
concepts and proofs.
• (iii) Objectivity reinterpreted as social and intersubjective.
Objective knowledge understood as social, cultural, public
and collective knowledge (not personal, private or
individual belief) following Bloor and Harding
• (iv) Adopts conversation as the basic underpinning
representational form for its epistemology. Thus views
mathematics as basically linguistic/semiotic, embedded in
social world of human interaction.

15. CONVERSATION AND EPISTEMOLOGY
• Beyond metaphor of the 'great conversation'
conversation taken literally taken as a basic
epistemological form by many.
• our certainty about the Pythagorean Theorem
... Is a matter of conversation between
persons, rather than an interaction with
nonhuman reality. (Rorty)

16. Forms of Conversation in SC
INTRAPERSONAL
CONVERSATION
ORIGINAL FORM
INTERPERSONAL
CONVERSATION
CULTURAL
CONVERSATION
Thought as constituted
and formed by
conversation
Language games
situated in human
forms of life
Extended version:
creation and exchange
of texts in permanent
form
Thinking: internalised
conversation with
imagined other
Actual conversation:
based on shared
experiences,
understandings,
values, respect, etc.
Reading of any text:
dialogical, with reader
interrogating it and
creating answers from
it
All forms of conversation are social in manifestation
(interpersonal and cultural) or origin (intrapersonal)

17. Conversational Nature of Mathematics
• Conversation – underlying form of ebb and flow,
alternation of voices in assertion and counter assertion.
• Conversation is the source of feedback, in the form of
acceptance, elaboration, reaction, criticism and correction
essential for all human knowledge and learning
Different conversational roles originate in the interpersonal
but occur in all forms:
• Proponent / friendly listener following line of thought or
thought experiment sympathetically, for understanding
• Critic - argument is examined for weakness and flaws.

18. Knowledge lives in the World
• Conversation based in language games and forms
of life (Wittgenstein).
• Conversation as epistemological basis re-grounds
mathematical knowledge in physically-embodied,
socially-situated acts of human knowing and
communication.
• Rejects Cartesian dualism of mind versus body,
knowledge versus the world.
• Acknowledges multiple valid voices and
perspectives on knowledge, leading to ethical
implications (cf. Habermas)

19. Mathematical Text is Conversational
• Mathematics primarily symbolic activity - to create, record and
justify its knowledge (Rotman).
• Viewed semiotically as comprising texts, maths addresses a reader.
In all cases the word is orientated towards an addressee (Volosinov)
Maths texts, proofs use verb forms in indicative and imperative moods.
• Indicative mood for statements, claims, assertions describing future
outcomes of thought experiments for reader to perform or accept
• Imperatives are shared injunctions / orders issued by the to reader.
Reader of mathematics is either
• agent of mathematician's will, response is imagined / actual action
• critic seeking to make a critical response.
In all cases the mathematical text is conversational

20. Concepts Dialogical / Conversational
TOPIC DIALECTICAL CONCEPT
Analysis - definitions of the limit
Constructivist
Logic
Interpretation of quantifiers: xy...
"You choose x, and I show how to construct y"
Recursion theory Arithmetical Hierarchy - ...
Set theory Diagonal argument: for any enumeration, omitted
element
Set theory Game-theoretic version of Axiom of Choice
Game Theory Alternation of moves by opponents
Number theory J. Conway's game theoretic foundations of number
Statistics Hypothesis testing (H0 versus HA)
Probability Analysis of wagers, betting games

21. Knowledge Acceptance Conversational
• Proof structure is a means to epistemological end of persuading
mathematical community. A proof becomes a proof after the social
act of ‘accepting it as a proof’. (Manin)
• Acceptance depends on largely tacit criteria and informed
professional judgement.
• Likewise teacher's decision to accept mathematical answers from
student depends on professional judgement. Based on criteria
including rhetorical style, not just rigid rules of correctness.
Acceptance of mathematical knowledge depends on dual roles
developed and internalised through conversation :
• Proposer of would be new knowledge, or sympathetic reader /
listener
• Critical reader / listener: reviewer, assessor, gatekeeper

22. Generalised Logic of Maths Discovery
Conversational mechanism for acceptance / modification of maths knowledge
SCIENTIFIC CONTEXT for Stage n
Background scientific and epistemological context: problems, concepts,
methods, informal theories, proof criteria and paradigms, and meta-
mathematical views.
THESIS Stage n (i) Proposal of new/revised conjecture, proof, solution or theory.
ANTITHESIS Stage n (ii) Dialectical and evaluative response to the proposal:
• Critical Response
Counterexample, counter-argument, refutation, criticism of proposal
• Acceptance Response
Acceptance of proposal. Suggested extension of proposal.
SYNTHESIS Stage n (iii) Re-evaluation and modification of the proposal:
• Local Restructuring Modified proposals: new conjecture, proof, problem-
solution, problems or theory.
• Global Restructuring of Context: changed problems, concepts, methods,
informal theories. Changed proof paradigms, criteria, meta-mathematical
views.
OUTCOME Stage n+1 (i)
Accepted or rejected proposal, or revised scientific / epistemological context.
(Generalisation of Lakatos’ LMD to overcome criticisms.)

23. Context of Discovery and Justification
• Lakatos' Logic of Mathematical Discovery (and GLMD) shows
that proof (and concept) criticism and improvement is central to
the business of mathematics. (Manifested in conversation)
• This process is socially situated, and cannot be divorced from
context. Both proof-structure and its social function of
persuasion essential for warranting mathematical knowledge.
tacit or craft knowledge is involved in these judgements.
• Critical scrutiny of proof by the mathematical community leads
to either
(a) criticism, requiring development and improvement (context
of discovery), or
(b) acceptance as a knowledge warrant (context of justification)
• The same Logic of Mathematical Discovery is at work in both
cases. There can be no proofs in mathematics which are above
critical scrutiny and this Logic, no matter how rigorous.

24. Conversation in Social Construction of Maths

25. Conversational Roles
In research mathematics, individuals use personal knowledge to
• Construct mathematical knowledge claims (possibly jointly),
• Participate in the dialogical process of criticism and
warranting of others' mathematical knowledge claims.
In mathematics education individuals use personal knowledge
to direct and control mathematics learning conversation to
• Present mathematical knowledge representations to learners
directly or indirectly (i.e. teaching), and
• Warrant and critique others' maths knowledge claims /
performances (i.e. assessment of learning).
Ultimately, individuals emerge with their personal knowledge
warranted (certified), and potentially able to participate in
these conversations as teachers or mathematicians

26. Expanded View of Maths Knowledge
Expanded View of personal Maths Knowledge (Kuhn, Kitcher ,
Ernest)
Mainly explicit components
• Accepted propositions & statements
• Accepted reasonings & proofs
• Problems and questions
Mainly tacit components
• Language and symbolism
• Meta-mathematical views: proof & definition standards, scope &
structure of mathematics
• Methods, procedures, techniques, strategies
• Aesthetics and values

27. Implications for Maths & Education
• Central role of conversation and language - both its use and
extended representational forms - in maths and education
• Mathematical knowledge includes a tacit or craft concrete
dimension: knowledge of instances and exemplars of problems,
situations, calculations, arguments, proofs, applications, etc.
• Maths problem solving depends on concrete knowledge of
instances of past problem solutions (Schoenfeld).
• Mathematical craft-knowledge of concrete particulars and instances
is vital in mathematics and learning mathematics
- contrary to widely held view that over-emphasises abstract and
general knowledge and neglects concrete and specific knowledge.
• This has significant implications for both epistemology and
mathematics education
• tacit or craft knowledge plays a central role in the mathematics and
teaching conversations, especially in the warranting of would-be-
knowledge and assessment of learning

28. Situated Views of Maths & Learning
• tacit and craft knowledge learned in the practices of a
culture. Embedded in shared social 'forms of life'
(Wittgenstein)
• Need not be seen as exclusively sited in an individual
mind, as assumed by cognitivism and constructivism
• Some developments in philosophy, psychology and
mathematics education assume this, e.g. 'situated
cognition' of Lave and Wenger, Vygotsky, Saxe,
Walkerdine, Harré, Shotter, Gergen, Mead etc.
• Tacit knowledge may be elicited in its context(s) of
origination as automatic component of engagement
with situation.

29. Vygotskian Space For Mind/Knowledge

30. Conversation in Vygotskian Space
Interpersonal
Conversation
Appropriation Surface Learning
Intrapersonal
Conversation (&
Interpersonal
Conversation)
Transformation Understanding – new
personal knowledge
Interpersonal Conversation Publication New utterance –
knowledge representation
Cultural Conversation Conventionalisation Warranted knowledge

31. Justification of Maths Knowledge
To be knowledge it must have a warrant or justification.
• tacit or craft knowledge validated by public performance and
demonstration. (To have knowledge is to have the power to give a
successful performance. Ayer).
• Parallel between justification of knowledge, and assessment of
learning. Identical for tacit or craft mathematical knowledge.
In assessment of learning:
• Explicit recall of propositions is low-rated
• The application of tacit or craft knowledge is rated higher, especially
the production of warrants for claims.
• Critical evaluation of knowledge productions very high-rated
(Necessary skill for teachers and mathematicians - in role of critic /
assessor. The role of critic is an important internalised
conversational role )

32. The Rhetoric of Mathematics
• 'rhetoric' is not mere ornament or manipulation or trickery.
It is persuasive discourse. In matters from mathematical
proof to literary criticism, scholars write rhetorically.
(Nelson et al.)
• Even in the most austere case, namely mathematics, a
rhetorical function is served by the presentation of the
proof. (Kitcher)
• The content and style of proofs and texts are judged with
reference to experience of mathematical tradition (i.e. tacit
and craft knowledge), rather than explicit criteria.
• Rhetorical styles vary for different mathematical
communities, throughout research (and school)
mathematics.

33. Criteria For Rhetoric of Maths Texts
Some key criteria for acceptance of a mathematical claim text:
• Use restricted technical language in conformity with accepted usage,
using the standard accepted mathematical notation
• Avoid deixis: pronouns (except we) or terms re context of utterance
• Use spare, clipped expressions with minimal grammatical conventions
observed, no superfluous prose used, formal symbols predominating.
• Be succinct and preferably short (length lessens acceptance likelihood)
• Use accepted models of style for ‘motivating’ prose, linking prose,
definition, exposition, proof, etc., at appropriate points in the texts
• Use standard methods of computation, transformation or proof
• Justify proof steps in accordance with accepted rhetorical practice
• Refer to standard theorems, results, definitions, texts, mathematicians.
• Relate any new problems, methods or results to recognised ones
• Express text to minimize its novelty, re-arrangement of known
elements.
• Provide a persuasive logical narrative establishing any claims.

34. Rhetoric of School Maths Texts
Accepted rhetorical style of school mathematical text typically:
• Uses a restricted technical language and standard notation
• Uses spare, minimal overall forms of expression.
• Uses certain forms of spatial organisation of symbols, figures and
text on the page (‘linear’ with side-illustrations)
• Avoids deixis (pronouns or spatio-temporal locators).
• Employs standard methods of computation, transformation or
proof.
When used in classroom by learner this style is strictly regulated
(according to local, tacit norms)
When applied to published text books the style subject to different
constraints (commercial, content as well as professional)

35. Rhetoric of the Classroom
Students work on symbolic tasks, writing text-sequences,
learning through oral/written teacher-pupil 'dialogue':
• 1. content: symbols, concepts, definitions, procedures,
etc.
• 2. rhetorical style for school mathematics in written,
symbolic, iconic and oral modes of representation.
• Rhetorical style incorporates public justifications: evidence
for teacher of the desired processes and concepts. formal
mathematical texts with no trace of authorial subject,
• Project / investigational / problem solving work involves
shift in rhetorical style to text including judgements and
thought processes of the mathematical subject (learner),
and writer may use pronouns (‘I’).

36. Varieties of Knowledge

37. Comparing School & Research Maths
• The overall scheme of social constructivism
integrates the formation and warranting of both
subjective and objective knowledge of
mathematics.
• These concern
• 1. The individual, in the context of education
(learning and assessment), and
• 2. Shared or social knowledge, in the context of
research maths (creation and warranting of
mathematical knowledge)
• There are many similarities and differences

38. Differences between (traditional)
school and research mathematics
SCHOOL
MATHEMATICS
RESEARCH
MATHEMATICS
Learning of existing
knowledge
Creation of new
knowledge
Studied by all children Done by a tiny group of
adults
A preparatory learning
activity
Based on the
preparatory activity
Interactions face-to-face Interactions at a distance
Matters only to the
learner
Becomes part of public
knowledge

39. Similarities Between (Traditional)
School and Research Mathematics
SCHOOL MATHEMATICS RESEARCH MATHEMATICS
Based on school texts Based on mathematics texts
Answers to school problems Answers to disciplinary
problems
Submitted to teacher Submitted to editor
Produced and validated by
conversational pupil-teacher
interaction
Produced and validated by
conversational mathematician-
editor interaction
Acceptance depends on
judgement of teacher
Acceptance depends on
judgement of editor/referees
Judgement based on shared
tacit criteria of correctness and
values of school mathematics
culture
Judgement based on shared
tacit criteria of correctness and
values of research mathematics
culture

40. Contribution of Social Constructivism
IT PROPOSES THAT:
• 1. Mathematical knowledge is necessary, stable and
autonomous, but that
• 2. This co-exists with its contingent, fallibilist3, and
historically shifting character.
As Vico said, re geometry: the only things we can know
completely are those we have made (because there is
nothing more to know beyond what we have
constructed).
Social Constructivism links both the learning of
mathematics and research in mathematics in an
overall scheme in which knowledge travels either
embodied in a person or in a text, and the processes
of formation and warranting in the two contexts are
parallel

41. Social Constructivism provides an explanation of how
• Mathematics & logic seem irrefutably certain, yet are
contingent, historical creations
• The objects of mathematics are cultural fictions
emerging from the use of mathematical language and
symbolism, yet seem so solid
• Mathematics is so unreasonably effective in providing
the conceptual foundations of our scientific theories
about the world
The central explanatory concept is emergence: the
evolutionary history of culture and the individual, and
the shaping role of conversation
For more complete arguments see
• Ernest, Paul (1998) Social Constructivism as a
Philosophy of Mathematics, Albany, New York: SUNY
Press.