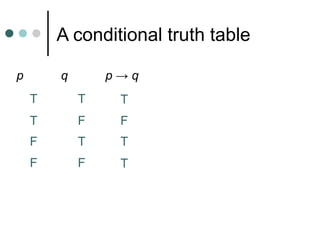
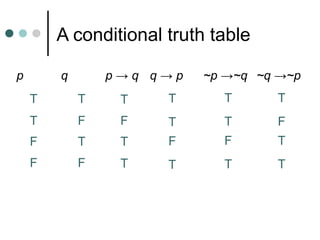
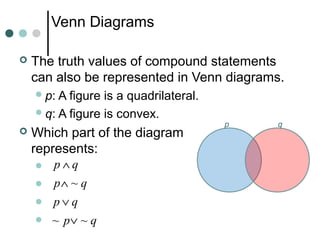
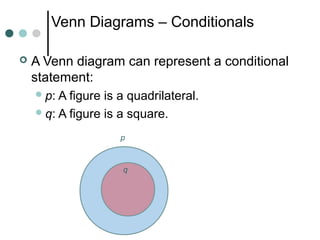
Inductive reasoning uses examples and observations to reach a conclusion, called a conjecture. A conjecture is either always true or false. While examples can support a conjecture, they cannot prove it. A counterexample can demonstrate that a conjecture is false.

1. Inductive Reasoning
Inductive reasoning is the process of using examples
and observations to reach a conclusion.
Any time you use a pattern to predict what will come
next, you are using inductive reasoning.
A conclusion based on inductive reasoning is called a
conjecture.

2. Counterexamples
A conjecture is either true all of the time, or it is false.
If we wish to demonstrate that a conjecture is true all
the time, we need to prove it through deductive
reasoning.
We will have more on deductive reasoning and the
proof process later. But for now, know that we can
never prove an idea by offering examples that support
the idea.
However, it can be easy to demonstrate that a
conjecture is false. We simply need to provide a
counterexample.

3. Intro to Logic
 A statement is a sentence that is either true or false
(its truth value).
 Logically speaking, a statement is either true or false.
What are the values of these statements?
 The sun is hot.
 The moon is made of cheese.
 A triangle has three sides.
 The area of a circle is 2πr.
 Statements can be joined together in various ways to
make new statements.

4. Conditional Statements
 A conditional (or propositional) statement has two parts:
 A hypothesis (or condition, or premise)
 A conclusion (or result)
 Many conditional statements are in “If… then…” form.
 Ex.: If it is raining outside, then I will get wet.
 A conditional statement is made of two separate
statements; each part has a truth value. But the overall
statement has a separate truth value. What are the values
of the following statements?
 If today is Friday, then tomorrow is Saturday.
 If the sun explodes, then we can live on the moon.
 If a figure has four sides, then it is a square.

5. Conditional Statements
 Conditional statements don’t have to be “If…
then…” See if you can determine the
condition and conclusion in each of the
following, and restate in “If… then…” form.
 An apple a day keeps the doctor away.
 What goes up must come down.
 All dogs go to heaven.
 Triangles have three sides.

6. Inverse
 The inverse of a statement is formed by
negating both its premise and conclusion.
 Statement:
 IfI take out my cell phone, then Mr. Peterson
will confiscate it.
 Inverse:
 If
I do not take out my cell phone, then Mr.
Peterson will not confiscate it.

7. Try these
 Give the inverses for the following
statements. (You may wish to rewrite as
“If… then…” first.) Then determine the truth
value of the inverse.
 Barking dogs give me a headache.
 If lines are parallel, they will not intersect.
 I can use the Pythagorean Theorem on right
triangles.
 A square is a four-sided figure.

8. Converse
 A statement’s converse will switch its
hypothesis and conclusion.
 Statement:
 If I am happy, then I smile.
 Converse:
 If I am happy, then I smile .

9. Try these
 Give the converses for the following
statements. Then determine the truth value
of the converse.
 If I am a horse, then I have four legs.
 When I’m thirsty, I drink water.
 All rectangles have four right angles.
 If a triangle is isosceles, then two of its sides
are the same.

10. Contrapositive
A contrapositive is a combination of a
converse and an inverse. The premise
and conclusion switch, and both are
negated.
Statement:
If my alarm has gone off,
then I am awake.
Contrapositive:
If my alarm has not gone off,
not
then I am not awakenot .

11. Try these
 Give the contrapositives for the following
statements. Then determine its truth value.
 If it quacks, then it is a duck.
 When Superman touches kryptonite, he gets
sick.
 If two figures are congruent, they have the
same shape and size.
 A pentagon has five sides.
 Note: A contrapositive always has the same
truth value as the original statement!

12. Symbolic representation
 Logic is an area of study, related to math (and
computer science and other fields). In formal
logic, we can represent statements symbolically
(using symbols).
 Some common symbols:
p a statement, usually a premise
q a statement, usually a conclusion
→ or ⇒ creates a conditional statement
~ or ¬ negates a statement (takes its opposite)

13. Examples
 If p, then q p→q
 Inverse:
If not p, then not q ~ p →~ q
 Converse:
If q, then p
q→ p
 Contrapositive
If not q, then not p ~ q →~ p

14. Truth Table
 A truth table is a way to organize the truth
values of various statements.
 Ina truth table, the columns are statements
and the rows are possible scenarios.
 The table contains every possible scenario
and the truth values that would occur.
 Example: p ~p
T F
F T

15. A conditional truth table
p q p→q
T T T
T F F
F T T
F F T

16. A conditional truth table
p q p→q q→p ~p →~q ~q →~p
T T T T T T
T F F T T F
F T T F F T
F F T T T T

17. Logical Equivalents
 Two statements are considered logical
equivalents if they have the same truth
value in all scenarios. A way to
determine this is if all the values are the
same in every row in a truth table.

18. Logical Equivalents
 Which of the following statements are logically
equivalent?
p q p→q q→p ~p →~q ~q →~p
T T T T T T
T F F T T F
F T T F F T
F F T T T T

19. Conjunctions
 A conjunction consists of two statements
connected by ‘and’.
 Example:
 Water is wet and the sky is blue.
 Notation:
 A conjunction of p and q is written as p∧q

20. Conjunctions
 A conjunction is true only if
both statements are true.
Remember: the truth
p q p
^q value of a conjunction
T T T refers to the statement
as a whole.
T F F
Consider: “The sun is
F T F out and it is raining.”
F F F

21. Disjunctions
 A disjunction consists of two statements
connected by ‘or’.
 Example:
I can study or I can watch TV.
 Notation:
 A disjunction of p and q is written as p∨q

22. Disjunctions
 A disjunction is true if either
statement is true.
p q pvq Consider: “Timmy
goes to Stanton or he
T T T goes to Paxon.”
T F T
F T T
F F F

23. Biconditional
 A biconditional statement is a special type of
conditional statement. It is formed by the conjunction
of a statement and its converse.
 Example:
 If a quadrilateral has four right angles then it is a rectangle, and
if a quadrilateral is a rectangle then it has four right angles.
 Biconditional statements can be shortened by using “if
and only if” (iff.).
 A quadrilateral is a rectangle if and only if it has four right
angles.
 This is true whether you read it forwards or ‘backwards’.

24. Biconditional
 A good definition will consist of a
biconditional statement.
 Ex: A figure is a triangle if and only if it has
three sides.

25. Biconditional
 A biconditional is true when the
statements have the same truth value.
p q p↔q Consider: “Two distinct
coplanar lines are
T T T parallel if and only if
they have the same
T F F
slope.”
F T F “Our team will win the
playoffs if and only if
F F T
pigs fly.”

26. Venn Diagrams
 The truth values of compound statements
can also be represented in Venn diagrams.
 p: A figure is a quadrilateral.
 q: A figure is convex.
p q
 Which part of the diagram
represents:
 p∧q
 p∧ ~ q
 p∨q
 ~ p∨ ~ q

27. Venn Diagrams – Conditionals
 A Venn diagram can represent a conditional
statement:
 p: A figure is a quadrilateral.
 q: A figure is a square.
p
q