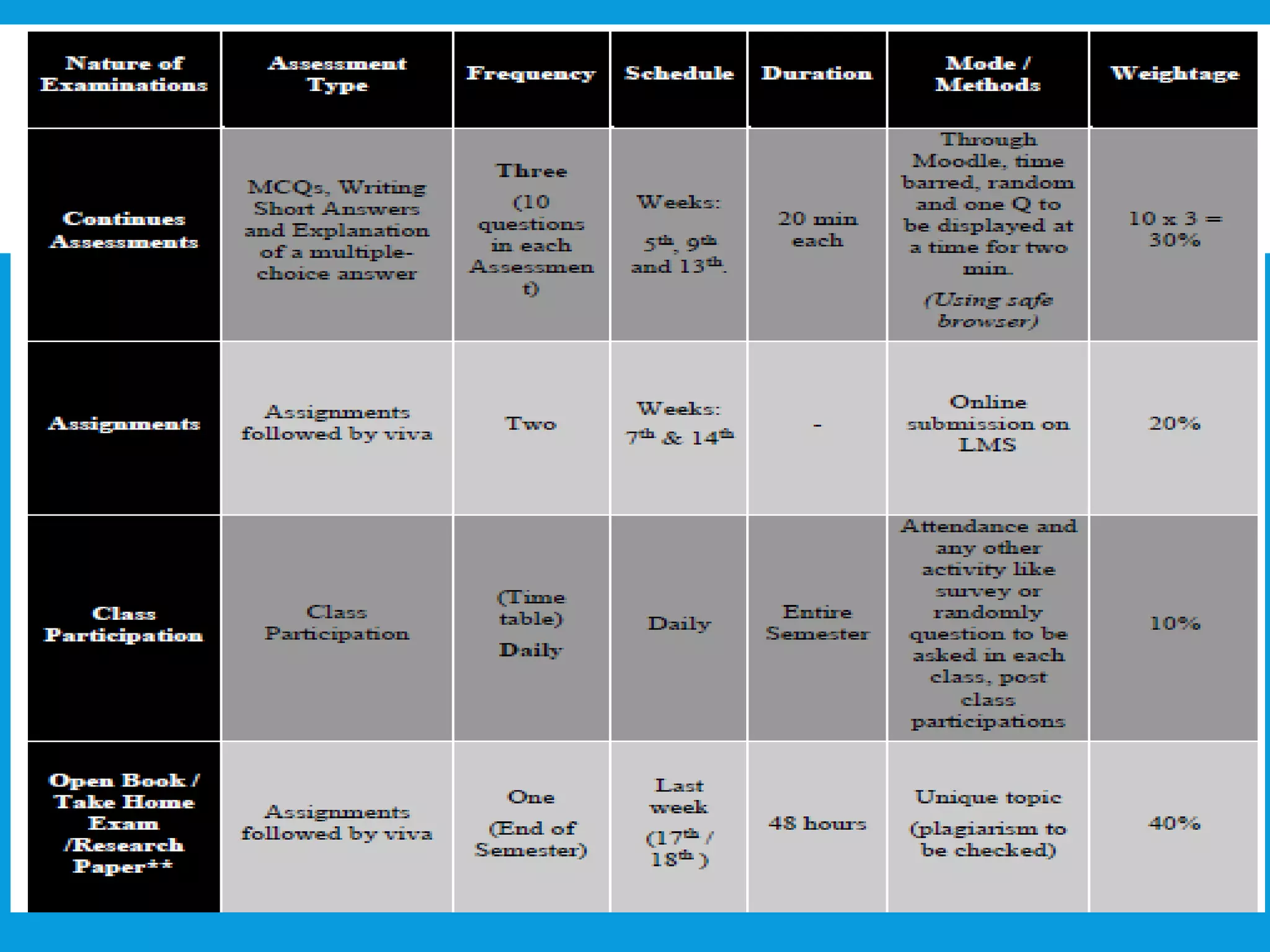
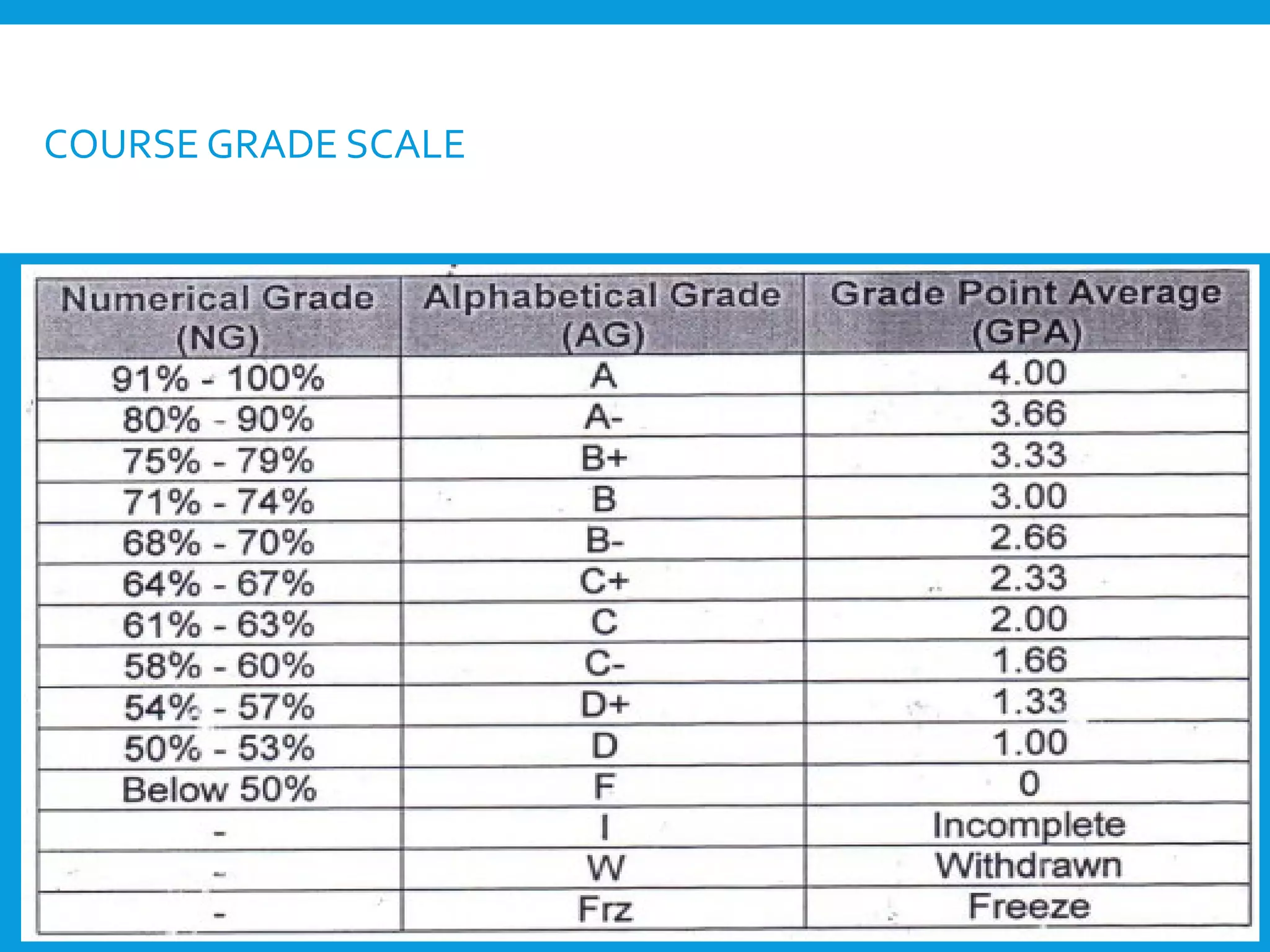
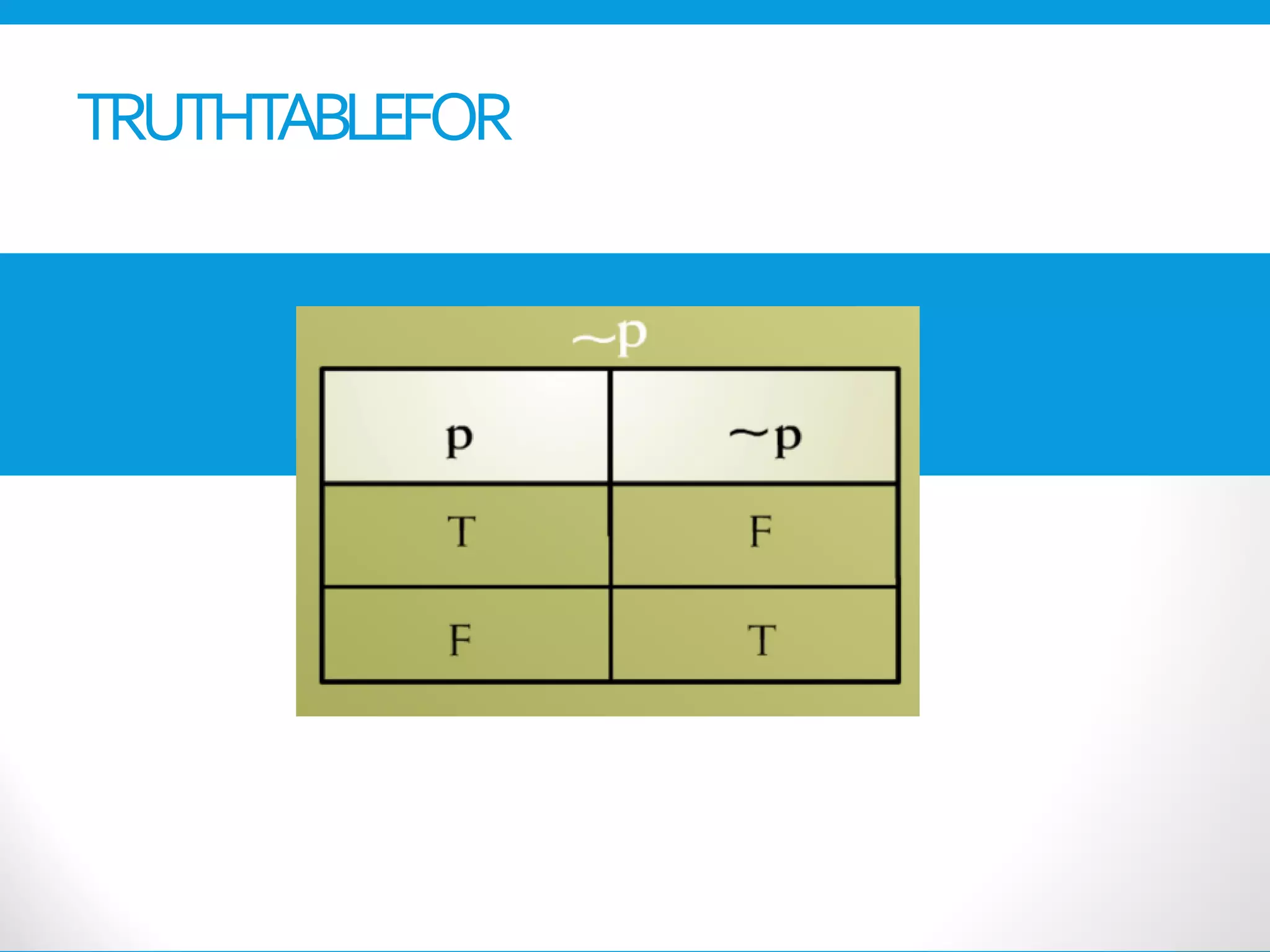
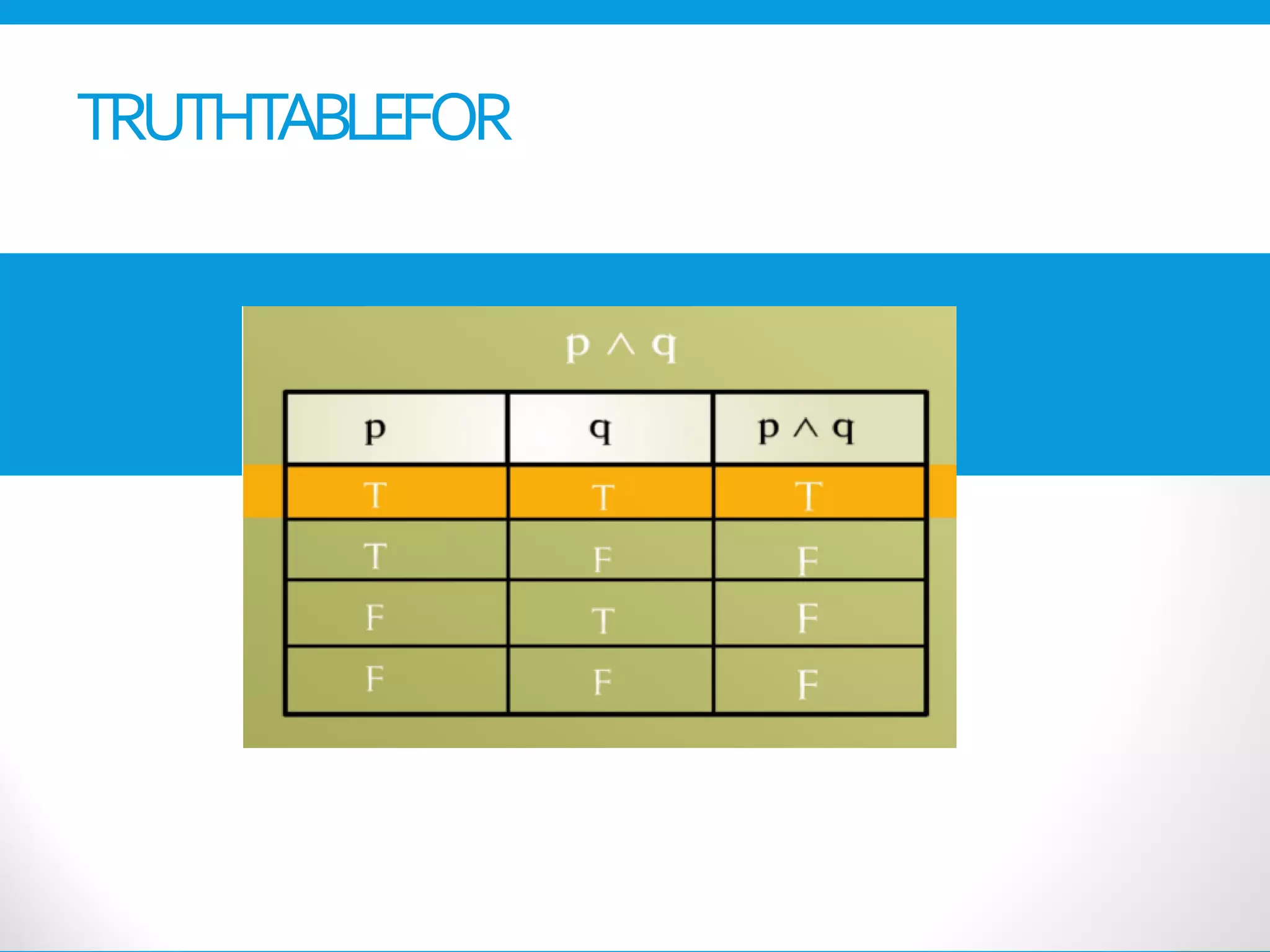
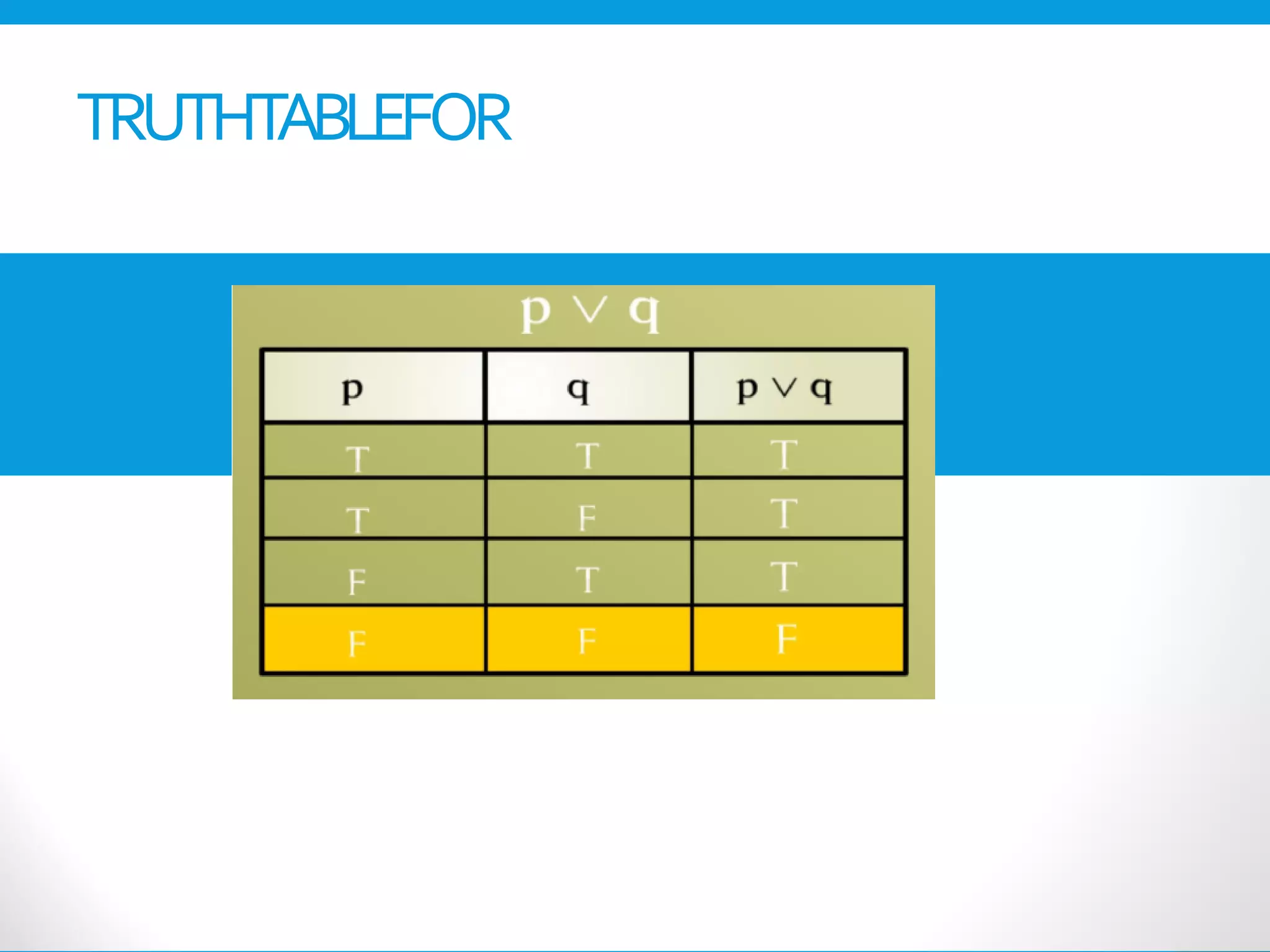
This document provides an introduction to the Discrete Structures course MAT-104. It includes the course objectives, which are to introduce topics like logic, set theory, functions, and graph theory. Active learning strategies like assignments and projects will be used. The course will be evaluated through quizzes, assignments, presentations, and a midterm and final exam. Policies around attendance and plagiarism are also outlined.

1. Sindh Madressatul Islam
University, Karachi
Department of Information
Technology

2. COURSE INTRODUCTION
Course Code
MAT-104
Course Title
Discrete Structure
Credit Hours
3+0 (3hr)

3. COURSE OBJECTIVES
 Mathematical reasoning: introduction to logic, propositional and
predicate calculus; negation disjunction and conjunction; implication
and equivalence; truth tables; predicates; quantifiers; natural
deduction; rules of Inference; methods of proofs; use in program
proving; resolution principle; Set theory: Paradoxes in set theory;
inductive definition of sets and proof by induction; Relations,
representation of relations by graphs; properties of relations,
equivalence relations and partitions; Partial orderings; Linear and
wellordered sets; Functions: mappings, injection and surjection,
composition of functions; inverse functions; special functions; Peano
postulates; Recursive function theory; Elementary combinatorics;
counting techniques; recurrence relation; generating functions. Graph
Theory: elements of graph theory, Planar Graphs, Graph Colouring,
Euler graph, Hamiltonian path, trees and their applications.

4. LEARNING STRATEGIES
Active learning strategies are employed in this course to encourage students'
participation in class and to foster their abilities to gather information and data
from its sources and analyze it.
Active learning strategies include assignments/projects where students work in
individual and in teams to solve certain problems. Readings may include many
Research Papers and other related studies.

5. RECOMMENDED RESOURCES
• Discrete Mathematical Structure with Application to
Computer Science, J. P. Temblay and B Manohar, McGraw-
Hill, 2nd Edition.
• Discrete Mathematics, 7th edition, Richard Johnson Baugh,
2008, Prentice Hall Publishers.
• Relevant Research Papers (Journal + Conference)

6. EVALUATION CRITERIA

7. COURSE GRADE SCALE

8. ATTENDANCE POLICY
• Students are expected to attend their classes. Absence never exempts a
student from the work required for satisfactory completion of the courses.
• Excessive absences of any course will result in:
 First warning for absence of 10% of the class hours
 Second warning for absence of 20% of the class hours
• A failing grade in the course for an absence of 25% of the class hours (as per
HEC guidelines)
• Exception to (3) may be made in the case of serious illness or death to an
immediate family member if approved by the dean of the college. In such
case, the student will receive a W grade in the course

9. PLAGIARISM
It is use of someone else’s idea, words, projects, artwork, phrasing, sentence
structure, or other work without properly acknowledging the ownership
(source) of the property.
Plagiarism is dishonest because it misrepresents the work of someone else as
ones own.
Students who are suspected of plagiarism will answer to an investigation
Those found guilty will face a disciplinary action as per the university
rules.

10. ASSESSMENT BREAKDOWN(THEORY)
100 MARKS
 Quizzes 10%
 Two + one quizzes
 Assignments 10%
 Two+One assignment
 Presentation 15%
 Class Participation/Attend. 05%
 Total 40%
 Mid term 20%
 Final 40%

11. OUTLINE
 Introduction to Discrete Structure
 Why Discrete Mathematics?
 Basic preliminaries

12. INTRODUCTIONTO DISCRETE
STRUCTURES

13. INTRODUCTION
 Discrete Structure describes processes that consist
of a sequence of individual steps, as compared to
forms of mathematics that describe processes that
change in a continuous manner. The major topics we
cover in this course are single-membership sets,
mathematical logic, induction, and proofs.

14. WHATISDISCRETEMATHEMATICS?
• Discrete mathematics focuses on problems that are not
over a continuous domain. For example, is it possible to
visit 3 islands in a river with 6 bridges without crossing
any bridge more than once? That is a discrete math
problem (because there are a finite (fixed, discrete)
number of bridges). Or, what is the smallest number of
telephone lines needed to connect 200 cities? The
numbers can be large and the logic can be complex, but
these type of problems are different from finding an
optimal value for a function where the domain can be 3,

15. WHATISDISCRETEMATHEMATICS?
• Discrete Mathematics concerns processes that
consist of a sequence of individual steps.

16. WHY DISCRETE STRUCTURE /
MATHEMATICS? (I)
 Computers use discrete structures to represent
and manipulate data.
 Computer Science is not Programming
 Computer Science is not Software Engineering
 Edsger Dijkstra: “Computer Science is no more
about computers than Astronomy is about
telescopes.”
 Computer Science is about problem solving.

17. WHY DISCRETE MATHEMATICS?
(II)
 Mathematics is at the heart of problem solving
 Defining a problem requires mathematical rigor
 Use and analysis of models, data structures,
algorithms requires a solid foundation of
mathematics
 To justify why a particular way of solving a
problem is correct or efficient (i.e., better than
another way) requires analysis with a well-defined
mathematical model.

18. PROBLEM SOLVING REQUIRES MATHEMATICAL
 Your boss is not going to ask you to solve
 an MST (Minimal SpanningTree) or
 aTSP (Travelling Salesperson Problem)
 Rarely will you encounter a problem in an abstract
setting
 However, he/she may ask you to build a rotation
of the company’s delivery trucks to minimize fuel
usage
 It is up to you to determine
 a proper model for representing the problem and
 a correct or efficient algorithm for solving it

19. Why Discrete Math?
Design efficient computer systems.
•How did Google manage to build a fast search engine?
•What is the foundation of internet security?
algorithms, data structures, database,
parallel computing, distributed systems,
cryptography, computer networks…
Logic, sets/functions, counting, graph theory…

20. What is discrete mathematics?
logic, sets, functions, relations, etc
Logic: artificial intelligence (AI), database, circuit design
Counting: probability, analysis of algorithm
Graph theory: computer network, data structures
Number theory: cryptography, coding theory

21. L
OGIC
Logicis the study of the principles and methods
that distinguishes between a valid and an invalid
argument.

22. STATEMENT

23. Topic 1: Logic and Proofs
Logic: propositional logic, first order logic
Proof: induction, contradiction
How do computers think?
Artificial intelligence, database, circuit, algorithms

24. Topic 2: Counting
• Sets
• Combinations, Permutations, Binomial theorem
• Functions
• Counting by mapping, pigeonhole principle
• Recursions, generating functions
Probability, algorithms, data structures

25. Topic 2: Counting
How many steps are needed to sort n numbers?

26. Topic 3: Graph Theory
• Relations, graphs
• Degree sequence, isomorphism, Eulerian graphs
• Trees
Computer networks, circuit design, data structures

27. Topic 4: Number Theory
• Number sequence
• Euclidean algorithm
• Prime number
• Modular arithmetic
Cryptography, coding theory, data structures

28. PROPOSITIONS
 A statement that has a truth value
 Which of the following are propositions?
 TheWashington State flag is red
 It snowed inWhistler, BC on January 4, 2008.
 Hillary Clinton won the democratic caucus in Iowa
 Space aliens landed in Roswell, New Mexico
 Ron Paul would be a great president
 Turn your homework in onWednesday
 Why are we taking this class?
 If n is an integer greater than two, then the equation an + bn = cn has no
solutions in non-zero integers a, b, and c.
 Every even integer greater than two can be written as the sum of two
primes
 This statement is false
– Propositional variables: p, q, r, s, . . .
– Truth values: T for true, F for false

29. TRUTHV
ALUESOFPROPOSITIONS

30. E
XAMPLES

31. E
XAMPLES

32. COMPOUND PROPOSITIONS
 Negation (not) ¬ p
 Conjunction (and) p ∧ q
 Disjunction (or) p ∨ q
 Exclusive or p ⊕ q
 Implication p → q
 Biconditional p ↔ q

33. NOTPROPOSITIONS

34. LECTURE #2/WEEK #2
 Rules of Discrete Structure
 TruthTable

35. RULE

36. E
XAMPLE

37. E
XAMPLE

38. UNDERSTANDINGSTATEMENTS

39. UNDERSTANDINGSTATEMENTS

40. COMPOUNDSTATEMENT

41. SYMBOLICREPRESENTATION

42. LOGICALCONNECTIVES

43. E
XAMPLES

44. TRANSLATING FROM ENGLISHTO
SYMBOLS

45. TRANSLATING FROM ENGLISHTO
SYMBOLS

46. TRANSLATING FROM ENGLISHTO
SYMBOLS

47. TRANSLATING FROM ENGLISHTO
SYMBOLS

48. TRANSLATING FROM ENGLISHTO
SYMBOLS

49. NEGATION(~)

50. TRUTHTABLE

51. TRUTHTABLEFOR

52. CONJUNCTION(^)

53. TRUTHTABLEFOR

54. DISJUNCTION(ᴠ)

55. TRUTHTABLEFOR