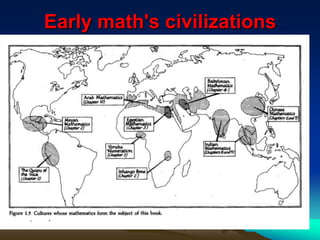
Mathematics has developed over thousands of years through contributions from many early civilizations. Key ideas emerged from cultures like the Babylonians with their number systems, Egyptians with practical applications of math, Indians who developed the base-10 system, and Greeks who made advances in geometry, astronomy, and formalizing math. Islamic mathematicians also made important contributions, especially in algebra. The study of math history can help students by putting a human face on the subject and showing how concepts developed to further understanding. It also provides motivation and opportunities to investigate. Philosophy of math examines questions around what math is, what is means for objects to exist in math, and how knowledge is acquired in the field.

2. Like the crest of a
peacock, like the
gem on the head of a
snake, so is
mathematics at the
head of all
knowledge

3. Dieudonné characterizes the
mathematician as follows:
we believe in the reality of
mathematics, but of course when
philosophers attack us with their
paradoxes we rush to hide behind
formalism and say "mathematics is
just a combination of meaningless
symbols" . . . Finally we are left in
peace to go back to our
mathematics, with the feeling each

4. What is Mathematics? (A
definition by) B. Russell
Mathematics may be defined as the
subject in which we never know what we
are talking about, nor whether what we
are saying is true.

5. What is Philosophy of
Mathematics?
 Formalism / Deductivism-
 is a school of thought that all work in mathematics should be
reduced to manipulations of sentences of symbolic logic, using
standard rules.
 It was the logical outcome of the 19th-century search for greater
rigor in mathematics. Programmes were established to reduce the
whole of known mathematics to set theory (which seemed to be
among the most generally useful branches of the science).
 First attempts to do this included those of Bertrand Russell and A.N.
Whitehead in Principia Mathematica (1910), and the later Hilbert
Programmes.

6. What is Philosophy of
Mathematics?(contd)
Ontology for Mathematics: “Being”
Ontology studies the nature of the
objects of mathematics.
It is the claim that mathematical
objects exist independently of their
linguistic expression.
“What we are talking about.”
• What is a point? line?
• What is a number?
• What is a set?
• In what sense do these objects exist?

7. What is Philosophy of
Mathematics?(contd)
Epistemology for Mathematics:
“Knowing”
Epistemology studies the acquisition of
knowledge of the truth of a
mathematical statement.
“whether what we are saying is true.”
 Does knowledge come from experience and evidence?
 Does knowledge come from argument and proof?
 Is knowledge relative or absolute?

8. What is Philosophy of
Mathematics?(contd)
According to Plato, knowledge
is a subset of that which is
both true and believed.

9. Semantic
 is a discipline concerned with inquiry into the meaning of
symbols, and especially linguistic meaning.
 Semantics in this sense is often contrasted with syntax,
 which deals with structures, and pragmatics,
 which deals with the use of symbols in their relation to
speakers, listeners and social context

10. Two Views of Mathematics Includes
Absolutist views of mathematics
Absolutism is a blanket term for several distinct views, which include: logicism,
formalism, constructivism
(intuitionism), Platonism and conventionalism.
Logicism is the thesis that mathematics is reducible to logic.
Advocates of logicism include: G.W. Leibniz (1646-1716), Gottolb Frege (1848-
1925). David Hilbert (1862-1943), John von Neumann (1903-1957) and Haskell
B. Curry are the main figures
associated with formalism. Formalism is so-named because its adherents see
mathematics as a formal
language. This school was dominant in the mid twentieth century.

11. Absolutist views of mathematics
(contd)
Immanuel Kant (1724-1804) and
Leopold Kronecker (1823-1891) are the
forebears of constructivism, though
the best-known constructivists are the
intutionists L.E.J Brouwer and Arend
Hevting,The constructivists contend is
invented not
discovered.Consequently,this is a
modified subgroup to absolutism
progressive absolutism.

12. Fallibilist views of mathematics

13. The development of
mathematical ideas
1. The mathematics we know today is the result of an
accumulation of content and processes developed
over a period of 4000 years;
2. Real people in early civilizations developed ideas
and ways to solve problems they faced in
agriculture, and needs for weights and measures,
religious worship, astronomy etc.
3. They invented number systems to help them make
calculations; geometry ideas to meet construction
needs etc.

14. Early math's civilizations

15. Spread of mathematical ideas

16. Mathematical Traditions:
1. Babylonian mathematics – large (base 60) number system
used to construct tables for calculations. Strong in Algebra.
Development of calendar.
2. Egyptian mathematics – used math's as practical tool in
agriculture (harvest & storage, control flooding. Geometry
strong. Devised & used Calendar. Fractions.
3. Indian mathematics – invention of the Number system
(base 10 system). Some geometry & trigonometry.
4. Greek mathematics – many famous names e.g. Plato,
Aristotle, Pythagoras, Thales. Greatest developments in
math ideas. Strongest in astronomy & geometry.
5. Arabic mathematics – Centered on Iran & Iraq. Algebra
was greatest contribution. Also astronomy & geometry.
Islamic religious rituals impacted development of geometry
& astronomy (moon).

18. Egyptian Mathematics
1. Used mathematics as practical tool to solve problems
e.g. construction, trade. Used calculations.
2. Calculations based on addition & 2x tables
3. Preferred unit fractions (⅓, ⅛, ½, ¼ etc.) – greater
accuracy
4. Trade: no currency but traded using goods such as
bread & beer
5. Much construction work e.g. canals, pyramids
6. Notable achievements – development of Lunar
Calendar; Pyramids

19. Indian Mathematics
1. Ancient Hindu society regarded as sacred & pure discipline.
Concealed math development & ideas.
2. Hindu Brahmins (highest caste) saw math's as related to
stars & planets, and the gods/heaven & hell.
Math knowledge & study accessible only to high-caste
children, so math was knowledge of the elite.
Greatest early mathematicians were Brahmins –
Brahmagupta, Mahavira, Bhaskara etc
3. Indian mathematicians known outside India – Ramanujan &
Shakuntala Devi – worked in number patterns & theorems

20. Greek Mathematics
1. Inherited legacy of accumulated knowledge from
Babylon & Egypt. Improved & perfected ideas into a
formal discipline of study – practical to abstract math's.
2. Greek were renowned astronomers
3. Important areas of discovery – Algorithms (how & why
they worked), Theorems & mathematical Proofs,
geometry, astronomy
Elements of Euclidean geometry ##
4. Schools of Plato, Aristotle & Pythagoras opened study
to women.
5. Greek mathematicians: Thales, Pythagoras, Aristotle,
Pascal

21. Math ideas from Europe
1. Bernoulii – brilliant math family from Netherland
2. Euler – son of Protestant minister. Was minister but studied
mathematics. Renowned for Algebra, Calculus
3. Laplace
4. Lagrange
5. Fourier
6. Gauss
7. Hardy
8. Polya – Problem solving
9. Von Neumann
etc

22. Famous Women Mathematicians
1. HYPATIA (Greek) - First woman
mathematician. Daughter of renowned
Prof of Math. Well educated, trained in
arts, literature, science & philosophy.
University lecturer, author, philosopher,
mathematician. Executed by the
Christian church.
2. MARIA AGNESI (Italian) – daughter of
Prof of Math. Private tutoring, highly
educated. University position.
3. SONYA KOVALESKY (Russian) –

23. Famous Men Mathematicians
1. Pythagoras of Samos (Greek) known for the
Pythagoras theorem used in trigonometry.
2. Andrew Wiles know for his proof of Fermat’s
Last Theorem.
3. Isaac Newton and Wilhelm Leibniz both know as
the ‘inventor’ of modern infinitesimal calculus.
4. Euclid known as the Father of Geometry and his
magnum opus.

24. Some mathematical history ideas
1. Number systems in India & Babylon, and now
2. Multiplication methods in Egypt & India, & now
3. Fractions in Egypt.
4. A mathematics problem from India
5. Tangrams (puzzles) & Abacus from China
6. Fractions as 2 numbers, numerator / denominator from
China
7. Algebra in Arab countries
8. The Calendar in Babylon, Egypt, and now
9. Geometry (Pythagoras, Euclid) in Greece
10. Finger counting in Africa
11 Measurement by body parts e.g PNG, Fiji etc.
12 Counting systems e.g. Fijian society

25. How can “history” ideas help mathematics learning?
Gives mathematics a human face
Make mathematics less frightening
Showing pupils how concepts developed will
help their understanding.
Changes pupils’ ideas of mathematics.
Increases motivation for learning.
Provides opportunities for investigation.
Past obstacles help to explain what today’s pupil
find hard.

26.  Pupils derive comfort from realizing that they are not the only one
with problems.
 Encourages fast learners to look further.
 Helps develop a multicultural approach.
 Helps math's teacher to maintain excitement & interest in math's.
 Explains the role of math's in society.
 Indicates link between math's & other subjects
 Very good way of introducing a lesson

27. Ways of using ”history” in class.
 As anecdotes (short, amusing or personal accounts) during the
lesson.
 Link concepts they’re learning as answers to historical problems
faced in the past.
 As a drama to demonstrate the mathematical interaction.

28. Ways of using ”history” in class
(contd)
As classroom or homework exercises
Poster displays and projects with a historical theme.
Use examples to illustrate particular techniques or
methods in the past e.g. multiplication.
Use errors and alternative views from the past to
help resolve difficulties today

29. Roles for Philosophy of in Teaching and Learning
Roles for Philosophy in Teaching and Learning
For the Teacher/Mentor (T/M)
 Awareness of issues can alert the T/M to excessively authoritarian
approaches.
 Alternative philosophical views can allow the T/M to use and/or
develop alternatives to traditional approaches.
 Philosophical issues can illuminate the value of and need for
developing a variety of mathematical tools for “solving problems”.

30. Roles for Philosophy in
Teaching and Learning
For the Student/Learner (S/L)
Helps the S/L understand the context,
goals, and objectives of the mathematics
being studied.
Opens the S/L to considerations of the
human values and assumptions made in
developing and using mathematics.
Alerts the S/L to the use of authority and
the value of different approaches to
mathematics.