The document discusses the foundations of propositional logic, focusing on variables, domains, predicates, and quantifiers, specifically universal and existential quantifiers. It explains the structure of predicate logic, including unary, binary, and n-ary predicates, as well as providing symbolic representations for various statements. Additionally, it addresses the truth values of predicate formulas, their interpretations, and criteria for validity in logical arguments.









![Preparedby:SharifOmarSalem–ssalemg@gmail.com
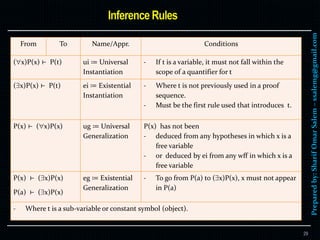
Predicate wffs can be built similar to propositional wffs using logical
connectives with predicates and quantifiers.
Examples of predicate wffs
(x)[P(x) Q(x)]
(x) ((y)[P(x,y) V Q(x,y)] R(x))
S(x,y) Λ R(x,y)
9](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-10-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
“Every person is nice”
can be rephrased as
“For any thing, if it is a person, then it is nice.”
P(x) ≔ “x is a person”
Q(x) ≔ “x is nice” the statement can be symbolized as
For any thing, if it is a person, then it is nice
(x) [ P(x) Q(x) ]
“All persons are nice” or “Each person is nice” will also have the
same symbolic formula.
always related with (implication)
10](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-11-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
“There is a nice person”
can be rewritten as
“There exists something that is both a person and nice.”
In symbolic form,
(x)[P(x) Λ Q(x)].
Variations: “Some persons are nice” or “There are nice persons.”
always related with Λ (conjunction)
What would the following form mean for the example above?
(x)[P(x) Q(x)] ???????
11](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-12-320.jpg)
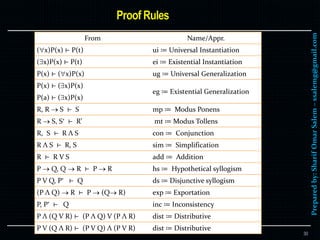
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Example for forming symbolic forms from predicate symbols
All dogs chase all rabbits ≔
For anything, if it is a dog, Then for any other thing, if it is a rabbit,
then the dog chases it ≔
(x)[ D(x) (y)( R(y) C(x,y) ) ]
12
D(x) ≔ “x is a dog”
R(y) ≔ “y is a rabbit”
C(x,y) ≔ “x chases y”](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-13-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Some dogs chase all rabbits ≔
There is something that is a dog and for any other thing, if that thing is a rabbit,
then the dog chases it ≔
(x)[D(x) Λ (y)(R(y) C(x,y) ) ]
Only dogs chase rabbits ≔
For any things, If it chase rabbits, then it is a dog.
≔ For any things and for any other things if the other things is rabbits and
chases by the first thing, then that first thing is a dog
≔ For any two things, if one is a rabbit and the other chases it, then the other is
a dog
≔ (y) (x)[R(y) Λ C(x,y) D(x)]
13
D(x) ≔ “x is a dog”
R(y) ≔ “y is a rabbit”
C(x,y) ≔ “x chases y”](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-14-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Everything is fun ≔ (x)A(x)
Negation will be “it is false that everything is fun,” ≔ [(x)A(x)]
i.e. “something is non-fun.” ≔ (x)[A(x)]
In symbolic form, [(x)A(x)] ↔ (x)[A(x)]
Similarly negation of “Something is fun” ≔ (x)A(x)
Negation will be “it is false that Something is fun,”
“Nothing is fun” ≔ [(x)A(x)]
i.e. “Everything is boring.” ≔ (x)[A(x)]
Hence, [(x)A(x)] ↔ (x)[A(x)]
14](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-15-320.jpg)

![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Write wffs that express the following statements:
All players are good.
Some good players, score goals.
16
For anything, if it is a player, then it is good ≔ (x)[S(x) I (x)]
There is something that is good and it is a player and it score goals
≔ (x)[I(x) Λ S(x) Λ M(x)]
S(x)≔ x is a player
I(x)≔ x is good
M(x)≔ x scores goals](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-17-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Everyone who scores goals is a bad player.
Only good player, scores goals.
17
For anything, if that thing scores goals, then it is a player and it is not good
≔ (x)[ M(x) S(x) Λ (I (x)) ]
For any thing, if it scores goals , then it is a player and it is good
≔ (x)(M(x) S(x) Λ I(x))
S(x)≔ x is a player
I(x)≔ x is good
M(x)≔ x scores goals](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-18-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Similar to a tautology of propositional logic.
Truth of a predicate wff depends on the interpretation.
A predicate wff is valid if it is true in all possible interpretations just like a
propositional wff is true if it is true for all rows of the truth table.
A valid predicate wff is intrinsically true
18
Truth values
True or false – depends on the truth
value of statement letters
True, false or neither (if the wff
has a free variable)
Intrinsic truth
Tautology – true for all truth values
of its statements
Valid wff – true for all
interpretations
Methodology
(Validity Porve)
Truth Table/Proof sequence using
rules
Proof sequence using
rules/others
Free Variable (x)[P(x,y) (y) Q(x,y)]
variable y is not defined for P(x,y) hence y is called a free variable. Such
expressions might not have a truth value at all.](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-19-320.jpg)


![Preparedby:SharifOmarSalem–ssalemg@gmail.com
(x)[P(x) V Q(x)] (x)P(x) V (x)Q(x)
Invalid, can prove by mathematical context by taking P(x) = x is even
and Q(x) = x is odd.
In that case, the hypothesis is true but not the conclusion is false
because it is not the case that every integer is even or that every integer
is odd.
21](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-22-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
22
P(x) ≔ x is a painter
L(x,y) ≔ x loves y
a ≔ Alice
b ≔ Bob
Alice is a painter. ≔ P(a)
Bob loves Alice ≔ L(b,a)
Alice loves Bob ≔ L(a,b)
Bob is not a painter ≔ ¬P(b) or [P(b)]˜
If Bobisapainterthen AlicelovesBob ≔ P(b)L(a,b)
BobisapainteronlyifAliceisnotapainter ≔ P(b) ¬P(a)](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-23-320.jpg)

![Preparedby:SharifOmarSalem–ssalemg@gmail.com
W(x) ≔ x is a worker
P(x) ≔ x is a painter
L(x,y) ≔ x loves y
a ≔ Alice
b ≔ Bob
Every painter loves Bob ≔ (x)[P(x) L(xb)]
Some worker is a painter ≔ (x)[W(x) ∧ P(x)]
Alice loves every worker ≔ (x)[W(x) L(ax)]
Some painters are not workers ≔ (x)[P(x) ∧ ¬W(x)]
No painters are workers ≔ (x)[P(x) ¬W(x)]
Not every painter loves Alice ≔ ¬(x)[P(x) L(x,a)]
24](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-25-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
W(x) ≔ x is a worker
P(x) ≔ x is a painter
L(x,y) ≔ x loves y
a ≔ Alice
b ≔ Bob
Every worker loves some painter ≔ (x){W(x) (y)[P(y) ∧ L(x,y)]}
Some painter loves some worker ≔ (x){P(x) ∧ (y)[W(y) ∧ L(x,y)]}
No worker loves every worker
≔ (x){W(x)
¬(y)[W(y)L(x,y)]}
EveryworkerwhoisalsoapainterlovesBob ≔ (x){[W(x) ∧ P(x)] L(x,b)}
Some worker loves both Bob and Alice ≔ (x){W(x) ∧ [L(x,b) ∧ L(x,a)]}
EveryworkerwholovesBobalsolovesAlice ≔ (x){[T(x) ∧ L(x,b)]L(x,a)}
25](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-26-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
What is the truth of the following wffs where the domain consists of
integers:
(x)[L(x) O(x)] where O(x) is “x is odd” and L(x) is “x < 10”?
26](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-27-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
What is the truth of the following wffs where the domain consists of
integers:
(x)[L(x) O(x)] where O(x) is “x is odd” and L(x) is “x < 10”?
Using predicate symbols and appropriate quantifiers, write the
symbolic form of the following English statement:
D(x) is “x is a day” M is “Monday” T is “Tuesday”
S(x) is “x is sunny” R(x) is “x is rainy”
Some days are sunny and rainy.
It is always a sunny day only if it is a rainy day.
It rained both Monday and Tuesday.
Every day that is rainy is not sunny.
27](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-28-320.jpg)


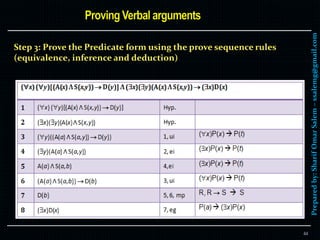
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Prove the following argument:
All flowers are plants. Sunflower is a flower. Therefore, sunflower is
a plant.
P(x) is “ x is a flower”
a is a constant symbol (Sunflower)
Q(x) is “x is a plant”
The argument is (x)[P(x) Q(x)] Λ P(a) Q(a)
The proof sequence is as follows:
32](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-33-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Prove the argument (x)[P(x) Q(x)] Λ [Q(y)] [P(y)]
Proof sequence:
Prove the argument (x)P(x) (x)P(x)
Proof sequence:
33](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-34-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Prove the argument (x)[P(x) Q(x)] Λ (x)P(x) (x)Q(x)
Proof sequence:
34](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-35-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Prove the argument
(x)[P(x) Λ Q(x)] (x)P(x) Λ (x)Q(x)
Proof sequence:
35](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-36-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Prove the argument
(y)[P(x) Q(x,y)] [P(x) (y)Q(x,y)]
Proof sequence:
36](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-37-320.jpg)

![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Prove the argument
[P(x) (y)Q(x,y)] (y)[P(x) Q(x,y)]
Proof sequence:
38](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-39-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Prove the Formula
[(x)A(x)] ↔ (x)[A(x)]
To prove equivalence, implication in each direction should be
proved
{[(x)A(x)] → (x)[A(x)]} Λ {[(x)A(x)] → (x)[A(x)]}
Proof sequence for [(x)A(x)] (x)[A(x)]
1. [(x)A(x)] hyp
2. A(x) temp. hyp
3. (x)A(x) 2, eg
4. A(x) (x)A(x) temp. hyp discharged
5. [A(x)] 1, 4, mt
6. (x)[A(x)] 5, ug
39](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-40-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Proof sequence for (x)[A(x)] [(x)A(x)]
1. (x)[A(x)] hyp
2. (x)A(x) temp. hyp
3. A(a) 2, ei
4. [A(a)] 1, ui
5. [(x)[A(x)]] 3, 4, inc
6. (x)A(x) [(x)[A(x)]] temp. discharged
7. [((x)[A(x)])] 1, dn
8. [(x)A(x)] 6, 7, mt
40](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-41-320.jpg)

![Preparedby:SharifOmarSalem–ssalemg@gmail.com
A(x) ≔ x is an ambassador
D(y) ≔ y is a diplomat
S(x,y) ≔ x speaks to y
Step 2: Convert verbal argument to predicate logic (hypothesis,
conclusion and form)
Every ambassador speaks only to diplomats
≔ For everyone and every others if this one is an ambassador
and he speaks to the other one, then that other one is a diplomat.
≔ (x) (y)[(A(x) Λ S(x,y)) D(y)]
42](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-43-320.jpg)
![Preparedby:SharifOmarSalem–ssalemg@gmail.com
A(x) ≔ x is an ambassador
D(y) ≔ y is a diplomat
S(x,y) ≔ x speaks to y
Some ambassadors speak to someone
≔ There exist someone and some others that this one is an
ambassador and he speaks to others.
≔ (x)(y)(A(x) Λ S(x,y))
there is a diplomat
≔ (x)D(x)
Argument formula
(x) (y)[(A(x) Λ S(x,y)) D(y)] Λ (x)(y)(A(x) Λ S(x,y))
(x)D(x)
43](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-44-320.jpg)

![Preparedby:SharifOmarSalem–ssalemg@gmail.com
Propositional Logic is not enough to describe properties and its related specs.
Predicate Logic Syntax are variables, quantifiers, predicate and connectives.
A collection of objects is called the domain of a variable.
Two kinds of quantifiers: Universal and Existential.
The collection of objects that satisfy the property P(x) is called the domain of
interpretation.
• always related with (implication)
• always related with Λ (conjunction)
• Negation of statements represented by the formula
[(x)A(x)] ↔ (x)[A(x)]
[(x)A(x)] ↔ (x)[A(x)]
Bound variable is the variable within the scope of the quantifier. Free variable is
the one out of the scope.
A predicate wff is valid if it is true in all possible interpretations
46](https://image.slidesharecdn.com/4formalmethodspredicatelogic-150221214933-conversion-gate02/85/4-formal-methods-predicate-logic-47-320.jpg)


