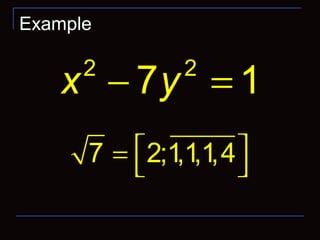This document summarizes continued fractions and their applications in number theory and combinatorial game theory. It defines general and simple continued fractions and explains how they can represent rational and irrational numbers. Finite simple continued fractions uniquely represent rational numbers, while infinite simple continued fractions represent irrational numbers. Continued fractions can be used to solve Pell's equation and find integer solutions. The document provides examples of representing numbers like π and√2 as continued fractions and using convergents of the continued fraction of √2 to solve the Pell equation x2 - 2y2 = 1.

1. Continued Fractions in
Combinatorial Game Theory
Mary A. Cox

2. Overview of talk
 Define general and simple continued fraction
 Representations of rational and irrational
numbers as continued fractions
 Example of use in number theory:
Pell’s Equation
 Cominatorial Game Theory:
The Game of Contorted Fractions

3. What Is a Continued Fraction?
 A general continued fraction representation of
a real number x is one of the form
 where ai and bi are integers for all i.
1
0
2
1
3
2
3 ...
b
x a
b
a
b
a
a
= +
+
+
+

4. What Is a Continued Fraction?
 A simple continued fraction representation of
a real number x is one of the form
 where
0
1
2
3
1
1
1
...
x a
a
a
a
= +
+
+
+
0ia >
ia +
∈Z

5. Notation
 Simple continued fractions can be written as
 or
[ ]0 1 2; , ,...x a a a=
0
1 2
1 1
...x a
a a
= +
+ +

6. Representations of
Rational Numbers

7. Finite Simple Continued Fraction
0ia >
0
1 2
1 1 1
...
n
x a
a a a
= +
+ +
[ ]0 1 2; , ,..., nx a a a a=

8. Finite Simple Continued Fraction
0ia >
1 1 1 1
3
4 1 4 2
x = +
+ + +

9. Finite Simple Continued Fraction
0ia >
1
3
1
4
1
1
1
4
2
x = +
+
+
+

10. Finite Simple Continued Fraction
0ia >
1
3
1
4
1
1
9/ 2
= +
+
+

11. Finite Simple Continued Fraction
0ia >
1
3
1
4
2
1
9
= +
+
+

12. Finite Simple Continued Fraction
0ia >
1
3
9
4
11
= +
+

13. Finite Simple Continued Fraction
0ia >
11
3
53
= +

14. Finite Simple Continued Fraction
0ia >
170
53
=

15. Theorem
 The representation of a rational number as a
finite simple continued fraction is unique (up
to a fiddle).

16. 170 1
3
153 4
1
1
1
4
2
= +
+
+
+

17. ( ) ( )
1
1
1 1 1
1
n
n n n
a
a a a
>
⇒ = − + = − +

18. 170 1
3
153 4
1
1
1
4
2
= +
+
+
+

19. 170 1
3
153 4
1
1
1
4
1
1
1
= +
+
+
+
+

20. [ ] [ ]
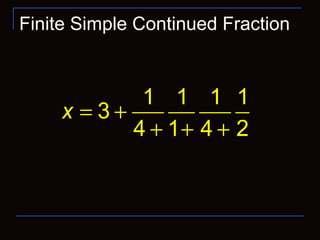
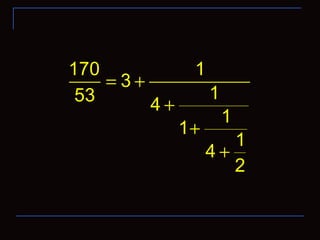
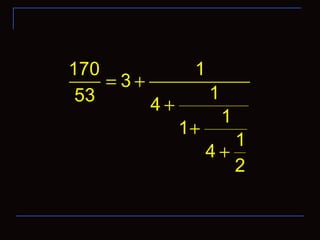
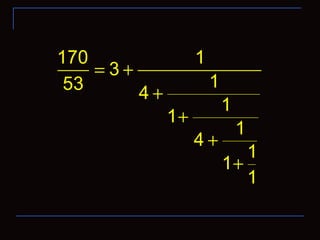
170
3;4,1,4,2 3;4,1,4,1,1
53
= =

21. Finding The Continued Fraction
19
51
x =

22. Finding The Continued Fraction
We use the Euclidean Algorithm!!
51 2 19 13
19 1 13 6
13 2 6 1
6 6 1 0
= ∗ +
= ∗ +
= ∗ +
= ∗ +

23. Finding The Continued Fraction
We use the Euclidean Algorithm!!
51 13
51 2 19 13 2
19 19
19 6
19 1 13 6 1
13 13
13 1
13 2 6 1 2
6 6
6
6 6 1 0 1
6
= ∗ + ⇔ = +
= ∗ + ⇔ = +
= ∗ + ⇔ = +
= ∗ + ⇔ =

24. 51 2 19 13
19 1 13 6
13 2 6 1
6 6 1 0
= ∗ +
= ∗ +
= ∗ +
= ∗ +
Finding The Continued Fraction
We use the Euclidean Algorithm!!

25. 19 1
0
151 2
1
1
1
2
6
= +
+
+
+
Finding The Continued Fraction

26. Finding The Continued Fraction
[ ]
19
0;2,1,2,6
51
=

27. Representations of
Irrational Numbers

28. Infinite Simple Continued Fraction
0ia >
0
1 2
1 1
...x a
a a
= +
+ +
[ ]0 1 2; , ,...x a a a=

29. Theorems
 The value of any infinite simple continued
fraction is an irrational number.
 Two distinct infinite simple continued
fractions represent two distinct irrational
numbers.

30. Infinite Simple Continued Fraction
[ ]3;7,15,1,292,...π =

31. Infinite Simple Continued Fraction
23 ?=

32. Infinite Simple Continued Fraction
 Let
 and
1 2
0 0 1 1
1 1
, ,...x x
x x x x
= =
− −      
0 0 1 1 2 2, , ,...a x a x a x= = =          

33. Infinite Simple Continued Fraction
23 4.8≈

34. Infinite Simple Continued Fraction
( )
( )
0
1
2
3
4
23 4 23 4
1 23 4 23 3
1
7 723 4
23 3
3
2
23 4
1
7
23 4 8 23 4
x
x
x
x
x
= = + −
+ −
= = = +
−
−
= +
−
= +
= + = + −
0
1
2
3
4
4
1
3
1
8
a
a
a
a
a
=
=
=
=
=

35. Infinite Simple Continued Fraction
23 4;1,3,1,8 =  

36. Theorem
 If d is a positive integer that is not a perfect
square, then the continued fraction expansion
of necessarily has the form:d
0 1 2 2 1 0; , ,..., , ,2d a a a a a a =  

37. Solving Pell’s Equation

38. Pell’s Equation
2 2
1x dy− =

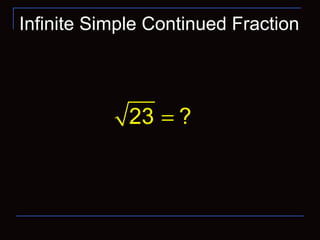
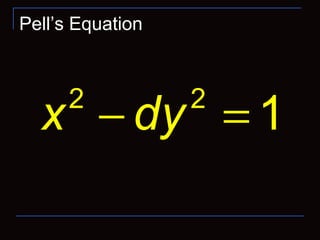
39. Definition
 The continued fraction made from
by cutting off the expansion after the kth
partial denominator is called the kth
convergent of the given continued fraction.
[ ]0 1 2; , ,...x a a a=

40. Definition
 In symbols:
[ ]0 1 2; , ,... ,1k kC a a a a k n= ≤ ≤
0 0C a=

41. Theorem
 If p, q is a positive solution of
 then is a convergent of the continued
fraction expansion of
2 2
1x dy− =
p
q
d

42. Notice
 The converse is not necessarily true.
 In other words, not all of the convergents of
supply solutions to Pell’s Equation.
d

43. Example
2 2
7 1x y− =
7 2;1,1,1,4 =  

44. Example
2
1
1
2 3
1
1 1 5
2
1 1 2
1 1 1 8
2
1 1 1 3
+ =
+ =
+
+ =
+ +
2 2
2 2
2 2
2 2
2 7 1 3
3 7 1 2
5 7 2 3
8 7 3 1
− ∗ = −
− ∗ =
− ∗ = −
− ∗ =