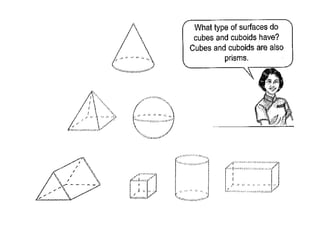
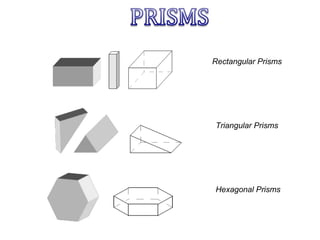
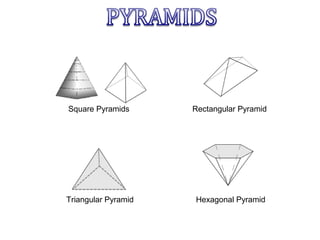
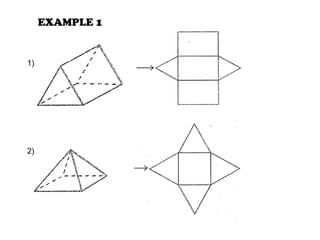
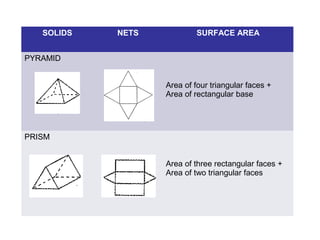
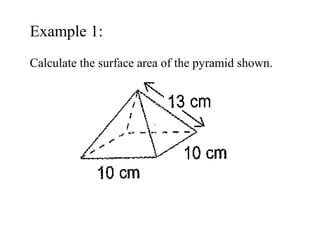
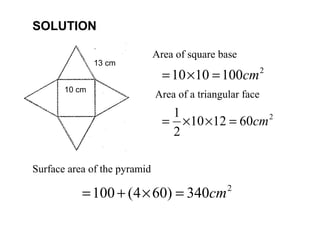
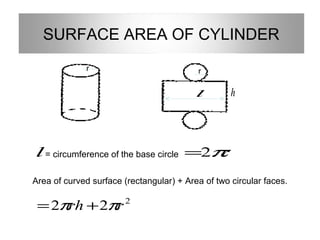
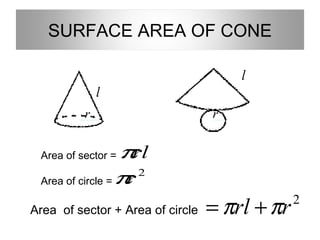
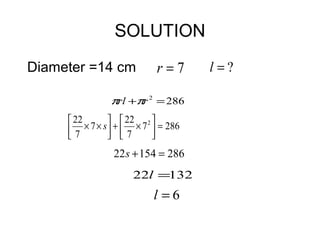
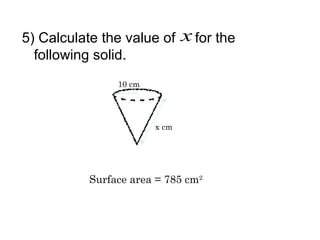
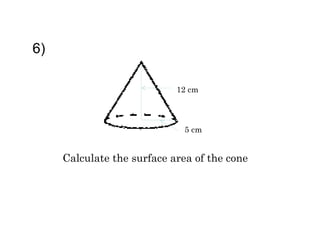
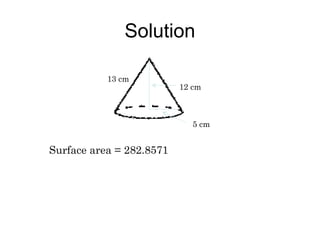
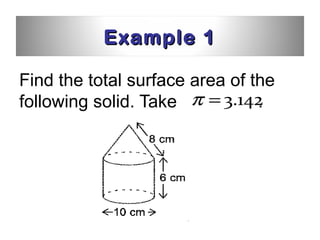
This document provides information about solid geometry, including definitions of different 3D shapes like prisms, pyramids, cylinders, cones, and spheres. It describes their key properties and provides examples. It also discusses nets, which are 2D shapes that can be folded into 3D solids. The document then covers calculating the surface areas of different solids and provides examples of solving surface area problems for prisms, cylinders, cones, and spheres. It concludes with practice problems for students to calculate surface areas.

1. What shape
can you see?

2. SOLID
GEOMETRY II

3. LEARNING OUTCOMES
State the geometric properties of prisms,
pyramids, cylinders, cones and spheres.
Draw nets for prisms, pyramids,
cylinders and cones.
State and find surface areas of prisms,
pyramids, cylinders, cones and spheres.

5. DEFINITION
Solid geometry is concerned with
three-dimensional shapes.
Some examples of three-dimensional
shapes are:
• Prisms
• Pyramids
• Cylinders
• Cones
• Spheres

6. 12.1 PROPERTIES
SOLIDS DESCRIPTION EXAMPLES
PRISM A solid with two congruent, parallel
bases which are polygons.
PYRAMID A solid with a base which is a polygon
and triangular sides that converge at a
vertex.
CYLINDER A solid with two parallel congruent
circular faces and a curved surface.
CONE A solid with a circular base and a
vertex.
SPHERE A solid having all of its points the same
distance from its centre.

7. Rectangular Prisms
Triangular Prisms
Hexagonal Prisms

8. Square Pyramids Rectangular Pyramid
Triangular Pyramid Hexagonal Pyramid

9. 5 faces
8 edges
5 vertices
2 faces
2 edges
1 vertices
5 faces
9 edges
6 vertices

10. 12.2 NETS OF GEOMETRIC
12.2 NETS OF GEOMETRIC
SOLIDS
SOLIDS
A net is a two-dimensional
figure that can be folded
into a three-dimensional
solid.

11. EXAMPLE 1
1)
2)

12. 3)
4)

13. WORKSHEET

14. 12.3 SURFACE AREA
The surface area of a solid is the
total area of all the faces of the
solid.
• It is measured using squares
• Units include mm²,cm²,m²,km².

15. SOLIDS NETS SURFACE AREA
PYRAMID
Area of four triangular faces +
Area of rectangular base
PRISM
Area of three rectangular faces +
Area of two triangular faces

16. Example 1:
Calculate the surface area of the pyramid shown.

17. SOLUTION
Area of square base
13 cm
= 10 × 10 = 100cm 2
10 cm
Area of a triangular face
1
= ×10 ×12 = 60cm 2
2
Surface area of the pyramid
= 100 + (4 × 60) = 340cm 2

19. SURFACE AREA OF CYLINDER
r r
l h
l = circumference of the base circle =2πr
Area of curved surface (rectangular) + Area of two circular faces.
= 2πrh + 2πr 2

20. Example
Find the surface area of a cylinder
with a radius of 7 cm and a height of
22
20 cm. (Take π=
7
)

21. SOLUTION
r = 7cm h = 20cm
Surface area of the cylinder
= 2πr + 2πrh
2
22 2 22
= 2( )(7 ) + 2( )(7)(20)
7 7
= 308 + 880 = 1188cm 2

22. SURFACE AREA OF CONE
l
l
r r
Area of sector = π rl
Area of circle = π
2
r
Area of sector + Area of circle = πrl + πr 2

23. Example
Calculate the surface area of a cone
with a radius of 5 cm and a slant
height of 8 cm. (Take π = 3.142)

24. SOLUTION
r = 5cm l = 8cm
Surface area of the cone
= πrl + πr 2
= (3.142)(5)(8) + (3.142)(52 )
= 204.23cm 2

25. SURFACE AREA OF SPHERE
Surface area of a sphere = 4πr
2
Where r is the radius of the sphere

26. Example:
Find the surface area of the sphere.
22
(Take π = )
7

27. SOLUTION
Surface area of the sphere:
22
= 4πr = 4 × × 3.52 = 154cm 2
2
7

28. POP QUIZ

29. 1) Find the surface area of the sphere
that has
3
a) radius = 1 m
11
b) diameter = 2.8cm

30. SOLUTION
3
a) r =1
11
2
22 14 
4πr 2 = 4 × × 
7  11 
= 20.3636
b) Diameter = 2.82
22 2.8 2
4πr = 4 ×
2
×( ) = 24.64
7 2

31. 2) Find the value of h for the solid
shown in the diagram if its surface
area is 1551 cm 2 .
22
Take π=
7
21 cm
h cm

32. SOLUTION
21
The solid given is cylinder. r= h=?
2
2πr 2 + 2πrh = 1551
 22  21  2   22 21 
 2 × ×    +  2 × × × h = 1551
 7 2   7 2 
 
693 + 66h = 1551
66h = 858
h = 13

33. 3) A cone has a base of diameter 14 cm.
Find the slant height of the cone if its
surface area 286 cm 2 .
22
Take π=
7

34. SOLUTION
Diameter =14 cm r=7 l =?
πrl +πr 2 = 286
 22   22 
7 × 7 × s  +  × 7 2  = 286
  7 
22 s + 154 = 286
22l =132
l =6

35. 4
4) A sphere has a surface area of 804 mm 2.
7
What is its radius?

36. Let r be the radius of the sphere.
Surface area of the sphere = 4πr 2
4
4π =804 mm 2
r 2
7
22 5632
4 × ×r =
2
7 7
88 2 5632
r =
7 7
r 2 = 64
r =8

37. 5) Calculate the value of x for the
following solid.
10 cm
x cm
Surface area = 785 cm2

38. SOLUTION
r =10
 22   22 
πrl + πr 2 =  ×10 × l  +  ×10 2  = 785
7  7 
220 2200
l+ = 785
7 7
220 3295
l=
7 7
l = 14.97

39. 6)
12 cm
5 cm
Calculate the surface area of the cone

40. Solution
13 cm
12 cm
5 cm
Surface area = 282.8571

41. 7) 2.8 mm
If the diameter of the iron rod is 2.8 mm and the
surface area of the rod is 2.8mm, find its length.

42. Solution
r =1.4
 22   22 2
2π rh + 2π r =  2 × × 1.4 × h +  2 × × (1.4)  = 892.32
2
 7   7 
8.8h +12.32 = 898.32
h = 100

44. Example 1
Find the total surface area of the
following solid. Take π = 3.142 .

45. Example 2
The solid shown below consists of a
cone and a hemisphere with a common
base. What is the total surface area of
=
the solid? Take π3.142 .
“Hemi”
means half.

48. HOMEWORK
• Ex12.3A, Ex12.3B, Ex12.3C
NEXT LESSON Chapter 13 - Statistics
http://www.harcourtschool.com/jingles/jingles_all/1what_am_i.html