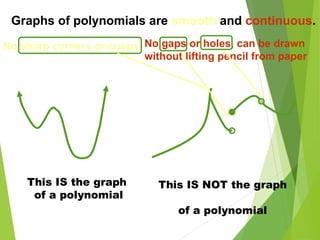
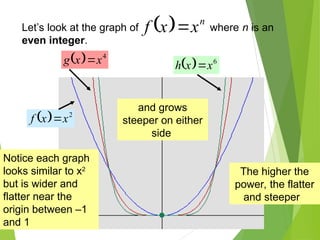
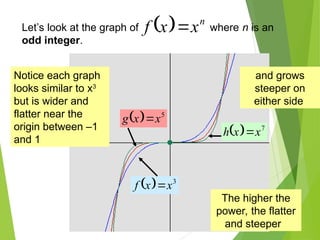
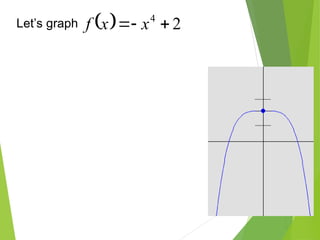
The document defines polynomials and polynomial functions, noting the importance of coefficients, degrees, and the distinction between polynomial and non-polynomial functions. It provides practice problems for identifying degrees, evaluating functions, and understanding the graphs of polynomials. The behavior of graphs for even and odd degrees is discussed, emphasizing their smooth and continuous nature.

3. Polynomials and Polynomial Functions
Definitions
Coefficient: the numerical factor of each term.
Constant: the term without a variable.
Term: a number or a product of a number and variables raised
to a power.
Polynomial: a finite sum of terms of the form axn
, where a is a
real number and n is a whole number.
2 2
3, 5 , 2 , 9
x x x y

2 2
9
, ,
5 2
x x x y

3, 6, 5, 32

3 2
15 2 5
x x
  
6 5 3
21 7 2 6
y y y y
  

4. A polynomial function is a function of the form:
  o
n
n
n
n a
x
a
x
a
x
a
x
f 



 
 1
1
1 
All of these coefficients are real numbers
n must be a positive integer
Remember integers are … –2, -1, 0, 1, 2 … (no decimals
or fractions) so positive integers would be 0, 1, 2 …
The degree of the polynomial is the largest
power on any x term in the polynomial.

5. Practice Problems
3 2
5 4 5
x x x
 
Identify the degrees of each term and the degree of the
polynomial.
3 2 1
3
9 6 2
6 3 0
Polynomials and Polynomial Functions
8
8
10
10

6. x 0
2
1
x
x 
Not a polynomial because of the
square root since the power is NOT
an integer
  x
x
x
f 
 4
2
Determine which of the following are polynomial
functions. If the function is a polynomial, state its
degree.
A polynomial of degree 4.
  2

x
g
  1
2 
 x
x
h
  2
3
x
x
x
F 

A polynomial of degree 0.
We can write in an x0
since this = 1.
Not a polynomial because of the x in
the denominator since the power is
negative 1
1 
x
x

7. Practice Problems
Evaluate each polynomial function
 
2
3 1
1 0
   3 1 10
   
3 10
 7

   
2
6 11 2
3 3 0
   

6 9 33 20
  
54 33 20
  87 20
  67
Polynomials and Polynomial Functions
  10
3 2

 x
x
f  
1

f
  20
11
6 2


 y
y
y
g  
3
g

8. Practice Problems

9. Simplify each sum and find the coefficient of
given term in the bracket
Remember
Use a zero as a placeholder for the
“missing” term.
Word Problem

10. Graphs of polynomials are smooth and continuous.
No sharp corners or cusps No gaps or holes, can be drawn
without lifting pencil from paper
This IS the graph
of a polynomial
This IS NOT the graph
of a polynomial

11. Let’s look at the graph of where n is an
even integer.
  n
x
x
f 
  2
x
x
f 
  4
x
x
g    6
x
x
h 
and grows
steeper on either
side
Notice each graph
looks similar to x2
but is wider and
flatter near the
origin between –1
and 1
The higher the
power, the flatter
and steeper

12. Let’s look at the graph of where n is an
odd integer.
  n
x
x
f 
  3
x
x
f 
  5
x
x
g 
  7
x
x
h 
and grows
steeper on
either side
Notice each graph
looks similar to x3
but is wider and
flatter near the
origin between –1
and 1
The higher the
power, the flatter
and steeper

13. Let’s graph   2
4


 x
x
f

14. Content, graphics and
Content, graphics and
text
text
belong to the rightful
belong to the rightful
owner.
owner.
No copyright intended
No copyright intended