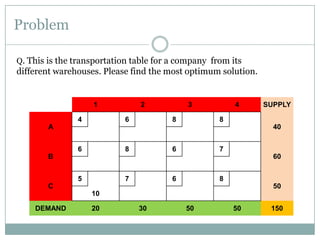
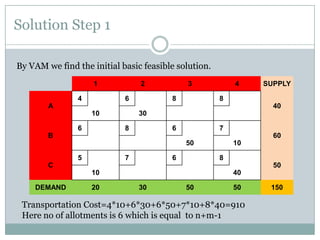
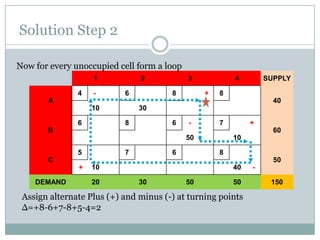
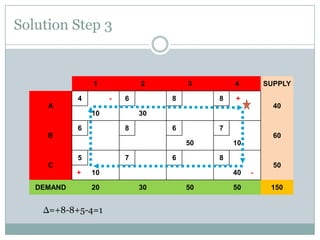
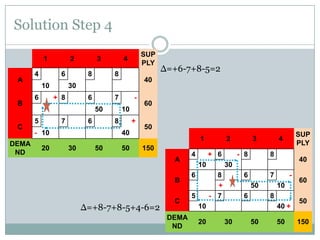
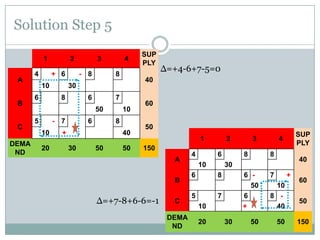
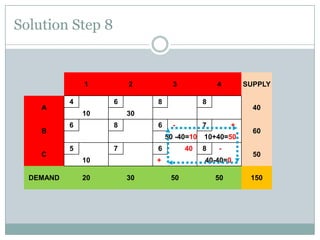
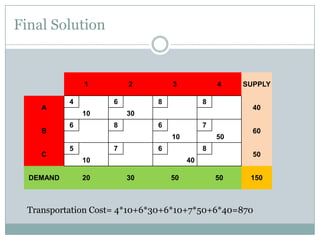
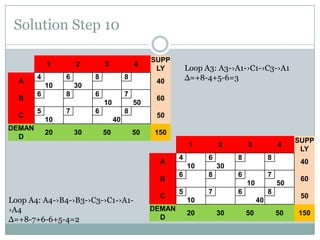
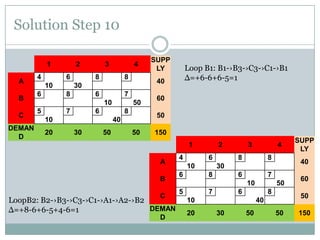
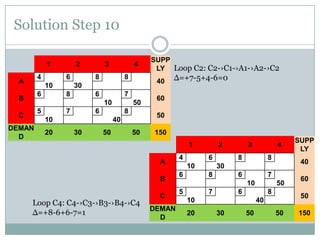
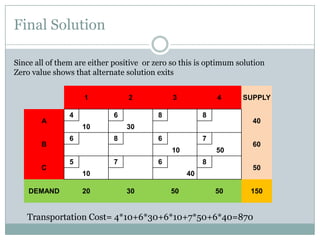
The stepping stone method is used to find the optimal feasible solution to a transportation problem after an initial basic feasible solution is found. It involves systematically checking each unused cell to see if shipping one additional unit to that cell would lower total transportation costs. This is done by forming closed loops around the cell and calculating the net change in cost. If a cell is found that lowers costs, units are reallocated until no further improvements can be made. The document provides an example problem that is solved step-by-step using this method, ultimately arriving at a lower optimal transportation cost than the initial basic feasible solution.

1. Transportation Problem:
Stepping Stone Method
MBA OIL & GAS 2013-2015

2. Stepping Stone Method
 Used to find Optimum feasible solution after finding




basic feasible solution by either North West Corner
Method (NWCM), Least Cost Method (LCM), Vogel’s
Approximation Method (VAM)
An Alternate method to MODI method to find
optimum solution
The Optimum solution by both will be the same.
The effect of unoccupied cells on transportation cost
is calculated
Every individual cell is tested to find the effect on
cost.

3. Steps Involved
 Start at any unused cell and trace a closed loop back
 Loop can turn only at occupied cells
 Only horizontal & Vertical moves allowed. No diagonal
movement
 Assign alternate plus (+) and minus (-) sign at the
corner cells
 Assign 1 unit of good at unused cell
 Calculate the “net change in cost” due to assignment
of 1 unit of good at unused cell by adding the cells
containing plus sign and subtracting the cells
containing minus sign

4. Problem
Q. This is the transportation table for a company from its
different warehouses. Please find the most optimum solution.
1
4
2
6
3
8
4
SUPPLY
8
A
40
6
8
6
7
B
60
5
7
6
8
C
50
10
DEMAND
20
30
50
50
150

5. Solution Step 1
By VAM we find the initial basic feasible solution.
1
4
2
6
3
8
4
8
A
40
10
6
30
8
6
7
B
60
50
5
7
6
10
8
C
50
10
DEMAND
SUPPLY
20
40
30
50
50
Transportation Cost=4*10+6*30+6*50+7*10+8*40=910
Here no of allotments is 6 which is equal to n+m-1
150

6. Solution Step 2
Now for every unoccupied cell form a loop
1
4
-
2
6
3
8
4
+
SUPPLY
8
A
40
10
6
30
8
6
-
7
+
B
60
50
5
7
6
10
8
C
50
+
DEMAND
10
20
40
30
50
50
Assign alternate Plus (+) and minus (-) at turning points
Δ=+8-6+7-8+5-4=2
150

7. Solution Step 3
1
4
2
-
6
3
8
4
8
SUPPLY
+
A
40
10
6
30
8
6
7
B
60
50
5
7
6
10
8
C
50
+
DEMAND
10
20
Δ=+8-8+5-4=1
40
30
50
50
150

8. Solution Step 4
1
A
B
C
DEMA
ND
4
2
6
10
6
3
8
8
6
7
50
7
6
20
10
8
- 10
+
40
30
50
Δ=+6-7+8-5=2
40
30
+ 8
5
SUP
PLY
4
50
60
50
1
150
A
B
Δ=+8-7+8-5+4-6=2
C
DEMA
ND
4
2
+ 6
10
6
8
6
7
40
30
50
6
10
8
10
20
SUP
PLY
4
- 8
8
+
- 7
5
3
40 +
30
50
50
60
50
150

9. Solution Step 5
1
A
B
C
DEMA
ND
4
2
+ 6
10
6
3
4
- 8
8
6
7
50
5
- 7
10
20
6
10
8
+
40
30
50
Δ=+4-6+7-5=0
40
30
8
SUP
PLY
50
60
50
1
150
A
B
Δ=+7-8+6-6=-1
C
DEMA
ND
4
2
6
10
6
8
6 50
6
+
7
40
30
7
10
20
SUP
PLY
4
8
8
5
3
30
50
+
10
8 40
50
60
50
150

10. Solution Step 6
 Each
Negative cost indicates the amount by which
transportation cost can be reduced by allocating one unit of
product were to be shipped from that source
 Choose the source which has most negative amount
 We can find maximum possible units which can be
transported by forming a loop
 Now for cell C 3 the value is negative so we will have to form
a loop and do reallocation of units

11. Solution Step 7
 The maximum quantity that can be shipped on the new
money-saving route can be found by referring to the closed
path of plus signs and minus signs drawn for the route and
selecting the smallest number found in those squares
containing minus signs
 To find the new solution add the smallest number to all the
squares with positive sign and subtract it from cells with
negative sign.
 Now again check the unoccupied cells for any negative
value.

12. Solution Step 8
1
A
B
C
DEMAND
4
2
6
10
6
3
4
8
8
6
-
7
50 -40=10
7
6
10
20
40
30
8
5
SUPPLY
40
+
30
+
10+40=50
8
-
40-40=0
50
50
60
50
150

13. Final Solution
1
A
B
C
DEMAND
4
2
6
10
6
3
4
8
8
6
7
10
5
7
50
6
8
10
20
40
30
8
50
60
50
40
30
SUPPLY
50
150
Transportation Cost= 4*10+6*30+6*10+7*50+6*40=870

14. Solution Step 10
1
A
B
C
DEMAN
D
4
2
6
10
6
3
4
8
8
6
7
10
5
7
8
10
20
50
6
50
60
50
40
30
Loop A3: A3-›A1-›C1-›C3-›A1
Δ=+8-4+5-6=3
40
30
8
SUPP
LY
50
150
1
A
B
Loop A4: A4-›B4-›B3-›C3-›C1-›A1›A4
Δ=+8-7+6-6+5-4=2
C
DEMAN
D
4
2
6
10
6
3
4
8
8
6
7
10
5
7
50
6
8
10
20
40
30
8
50
60
50
40
30
SUPP
LY
50
150

15. Solution Step 10
1
A
B
C
DEMAN
D
4
2
6
10
6
3
4
8
8
6
7
10
5
7
8
10
20
50
6
50
60
50
40
30
Loop B1: B1-›B3-›C3-›C1-›B1
Δ=+6-6+6-5=1
40
30
8
SUPP
LY
50
150
1
A
B
C
LoopB2: B2-›B3-›C3-›C1-›A1-›A2-›B2
DEMAN
Δ=+8-6+6-5+4-6=1
D
4
2
6
10
6
3
4
8
8
6
7
10
5
7
50
6
8
10
20
40
30
8
50
60
50
40
30
SUPP
LY
50
150

16. Solution Step 10
1
4
A
2
6
10
6
B
3
4
8
8
6
7
10
5
C
7
20
50
6
8
10
DEMAN
D
40
30
8
50
Δ=+7-5+4-6=0
60
50
40
30
SUPP
LY Loop C2: C2-›C1-›A1-›A2-›C2
50
150
1
A
B
Loop C4: C4-›C3-›B3-›B4-›C4
Δ=+8-6+6-7=1
C
DEMAN
D
4
2
6
10
6
3
4
8
8
6
7
10
5
7
50
6
8
10
20
40
30
8
50
60
50
40
30
SUPP
LY
50
150

17. Final Solution
Since all of them are either positive or zero so this is optimum solution
Zero value shows that alternate solution exits
1
A
B
C
DEMAND
4
2
6
10
6
3
4
8
8
6
7
10
5
7
50
6
8
10
20
40
30
8
50
60
50
40
30
SUPPLY
50
150
Transportation Cost= 4*10+6*30+6*10+7*50+6*40=870

18. Thanks!!!