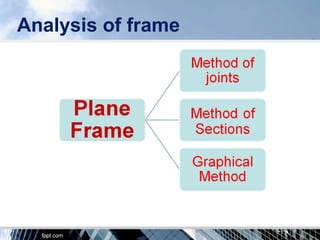
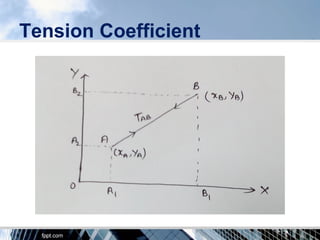
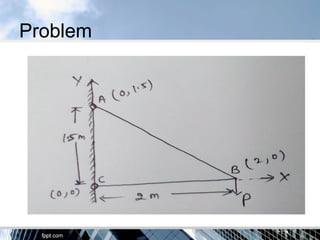
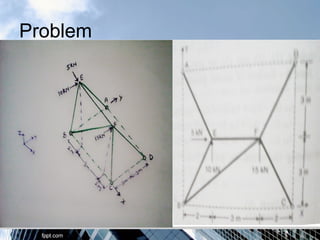
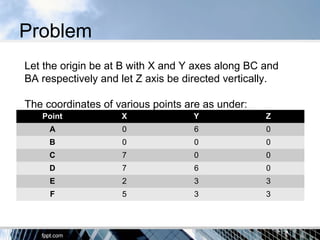
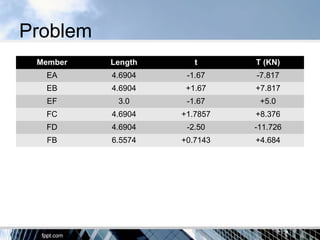
The document discusses the tension coefficient method for analyzing frames. The tension coefficient of a member is defined as the tension in the member divided by its length. Equilibrium equations are written at each joint using the tension coefficients and coordinates of the joints. Examples are provided to demonstrate how to set up and solve the equilibrium equations to determine the tension in each member for both plane and space frames under given loading conditions. Forces in all members of a sample space frame are calculated.

1. Unit-5
Tension Coefficient Method
Presented by : -DIVYA VISHNOI

2. Analysis of frame

3. Tension Coefficient Method
• Prof. R.V. Southwell introduce the Tension
Coefficient Method.
• It is systematic presentation of the method
of joints.
• This is specially useful for space frame.
• This method is valid for perfect frame.

4. Tension Coefficient
• The Tension Coefficient for a member of a
frame is defined as the pull or tension in
that member divided by its length.
t= Tension coefficient for the member
T= Pull in member
L= Length of the member
L
T
t =

5. Tension Coefficient

6. Tension Coefficient
• Consider a member AB of a pin jointed
perfect frame in equilibrium under a given
system of external forces (or reactions)
acting at the joint.
• be the resulting pull in the member.TAB

7. Tension Coefficient
Let (xA, yA) be the coordinate of A and (xB, yB) be the
coordinate of joint B
In X- direction,
TAB Cos = TAB
= TAB
= tAB*(xB- xA)

8. Tension Coefficient
In Y- direction,
TAB Sin = TAB
= TAB
= tAB*(yB- yA)
Note : -A member which is compression will have –ve tension coefficeint.

9. Analysis of Plane Frame
• Let us consider a joint A, where a no. of
members AB,AC,AD…….. etc are
meeting.
• Let PA is the external force acting at the
joint A and let xA & yA be the component of
this force P in X- direction and Y-direction.

10. Analysis of Plane Frame
Under equilibrium condition,
∑H=0
tAB×(xB - xA)+ tAC×(xC - xA)+ tAD×(xD - xA)+………..+XA =0
∑V=0
tAB×(yB - yA)+ tAC×(yC - yA)+ tAD×(yD- yA)+………..+YA=0
So,
∑t (xF - xN )+XA =0
∑t (yF - yN )+YA =0
(xF, yF )= Coordinate of far end
(xN, yN )= Coordinate of near end

11. Problem
• A plane frame consists of two members
AB and CB, hinged at A and C to the wall,
as shown in fig. Determine the forces in
the two members due to vertical force P
applied at joint B.

12. Problem

13. Problem
Let us consider origin at joint at C and CX and CY be the axes of
reference.
The coordinates of three joints are C(0,0) ; B(2,0) ; A(0,1.5).
There are only two members AB and CB.
So,
2.0 m (given)

14. Problem
At joint B,
∑H=0
tBA×(xA – xB)+ tBC×(xC – xB)+ 0=0
tBA×(0-2) + tBC× (0-2)=0
tBA+ tBC =0 ………………(1)
∑V=0
tBA×(yA – yB)+ tBC×(yC – yB)+ P=0
tBA× (1.5-0)+ tBC×(0-0)-P=0
1.5 tBA =P KN/m
From equ. (1) KN/m (-ve, means BC in Compression)

15. Problem
• Force in member BA = TAB = tBA×LBA
• Force in member BC = TBC = tBC×LBC

16. Analysis of Space Frame
• All concepts are similar as plane frame but
the coordinate system is in three
directions (X,Y,Z).
• So, the Formulas are;
∑t (xF - xN )+XA =0
∑t (yF - yN )+YA =0
∑t (zF - zN )+ZA =0
(xF, yF ,zF)= Coordinate of far end
(xN, yN, zN )= Coordinate of near end

17. Problem
• A space frame shown in fig. is supported
at A,B,C and D in a horizontal plane,
through pin joints. The member EF is
horizontal, and is at a height of 3m above
the base. The loads at the joints E and F,
shown un the fig. act in a horizontal
plane. Find the forces in all the members
of the frame.

18. Problem

19. Problem
Point X Y Z
A 0 6 0
B 0 0 0
C 7 0 0
D 7 6 0
E 2 3 3
F 5 3 3
Let the origin be at B with X and Y axes along BC and
BA respectively and let Z axis be directed vertically.
The coordinates of various points are as under:

20. Problem
Length of various members

21. Problem
Joint E: The three equations at joint E as follow:
tEA×(xA - xE)+ tEB×(xB - xE)+ tEF×(xF - xE)+XE =0
tEA×(0-2)+ tEB×(0-2)+ tEF×(5-2)+5 =0
-2tEA-2tEB+ 3tEF+5 =0 ……………….(1)
tEA×(yA - yE)+ tEB×(yB - yE)+ tEF×(yF - yE)+YE =0
tEA×(6-3)+ tEB×(0-3)+ tEF×(3-3)+10 =0
3tEA-3tEB+10 =0 ………………..(2)

22. Problem
tEA×(zA - zE)+ tEB×(zB - zE)+ tEF×(zF - zE)+ZE =0
tEA×(0-3)+ tEB×(0-3)+ tEF×(3-3) =0
-3tEA-3tEB =0 ………………..(3)
From (3) tEA=-tEB
From (2)
OR
From (1)

23. Problem
Joint F: The three equations at joint E as follow:
tFD×(xD – xF)+ tFC×(xC – xF)+ tFB×(xB – xF)+ tFE×(xE – xF)+XF =0
tFD×(7-5)+ tFC×(7-5)+ tFB×(0-5)+ tFE×(2-5) =0
2tFD+2tFC-5tFB-3 tFE =0 ……………….(4)
tFD×(yD – yF)+ tFC×(yC – yF)+ tFB×(yB – yF)+ tFE×(yE – yF)+YF =0
tFD×(6-3)+ tFC×(0-3)+ tFB×(0-3)+ tFE×(3-3)+15 =0
3tFD-3tFC-3tFB +15=0 ………………..(5)

24. Problem
tFD×(zD – zF)+ tFC×(zC – zF)+ tFB×(zB – zF)+ tFE×(zE – zF)+ZF =0
tFD×(0-3)+ tFC×(0-3)+ tFB×(0-3)+ tFE×(3-3) =0
-3tFD-3tFC-3tFB =0 ………………..(6)
By solving the equations (4), (5) and (6)
tFD = -2.5 KN/m
tFC = +1.7857 KN/m
tFB = +0.7143 KN/m

25. Problem
Member Length t T (KN)
EA 4.6904 -1.67 -7.817
EB 4.6904 +1.67 +7.817
EF 3.0 -1.67 +5.0
FC 4.6904 +1.7857 +8.376
FD 4.6904 -2.50 -11.726
FB 6.5574 +0.7143 +4.684

26. References
• SMTS-II, Theory of Structures, by “B.C.
Punmia” , ISBN:8170086183.
• Structural and Stress analysis, by “T.H.G.
Megson”, ISBN: 97-8008-099-936-4.
• www.iitg.ac.in/kd/Lecture
%20Notes/ME101-Lecture07-KD.pdf