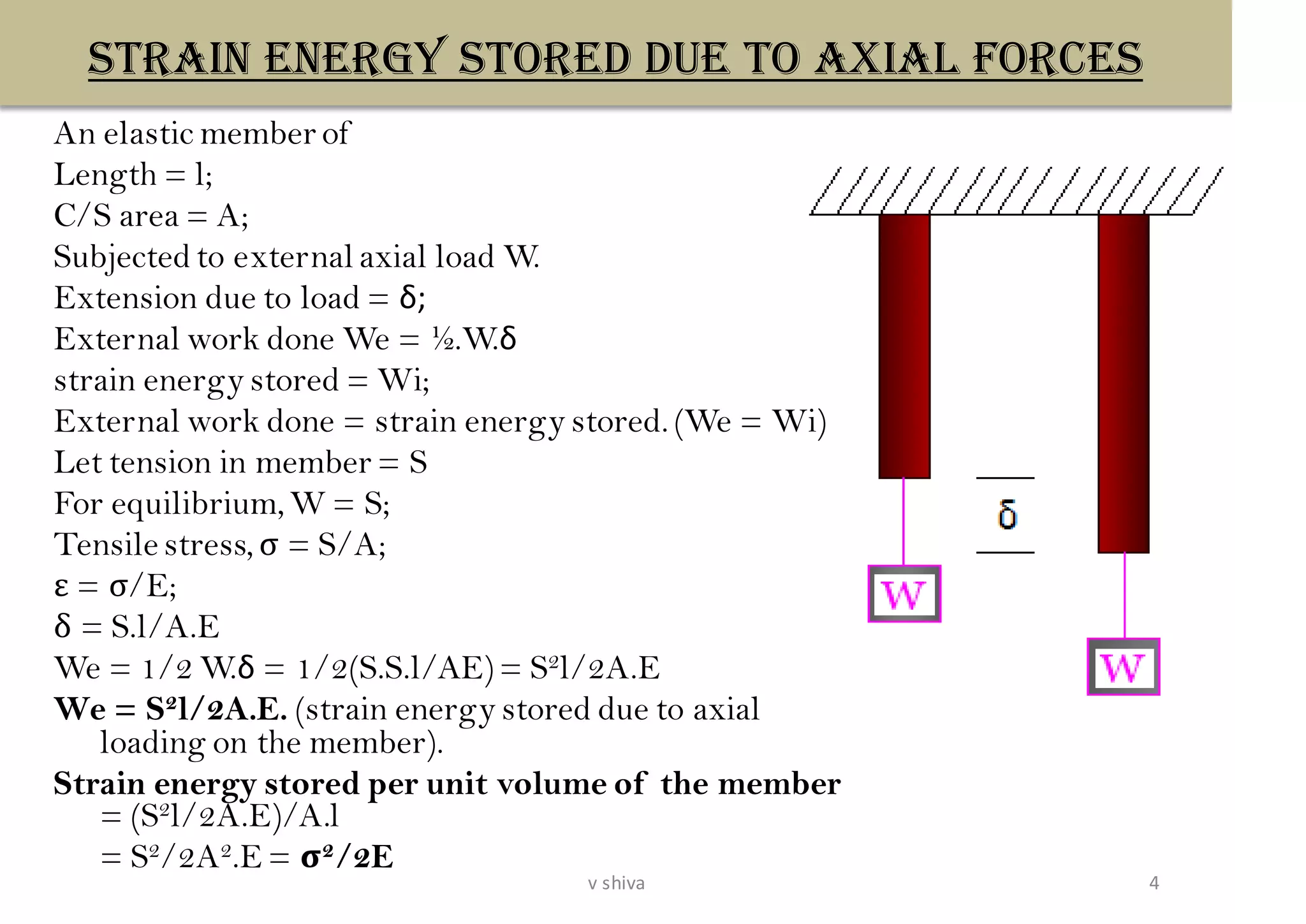
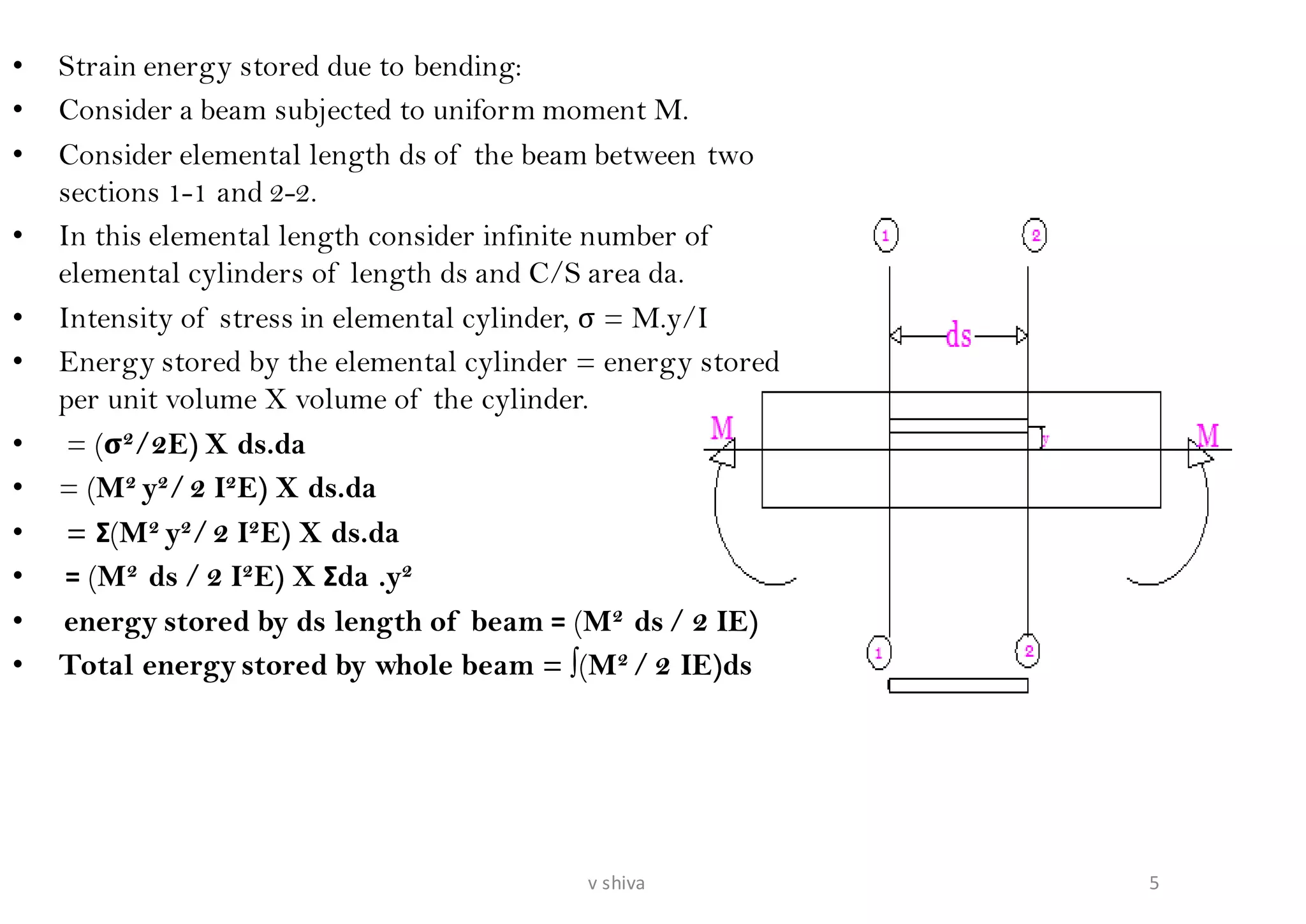
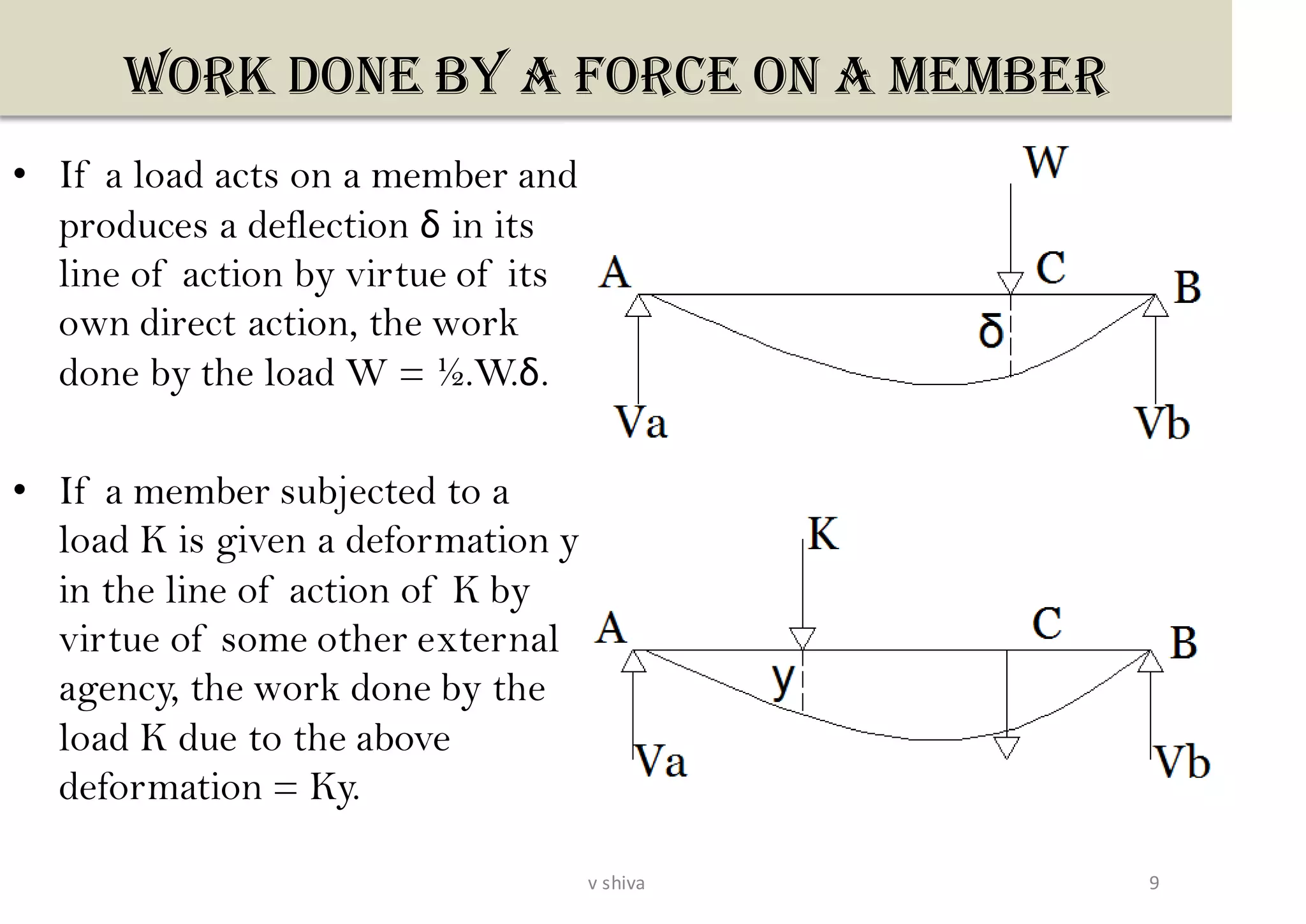
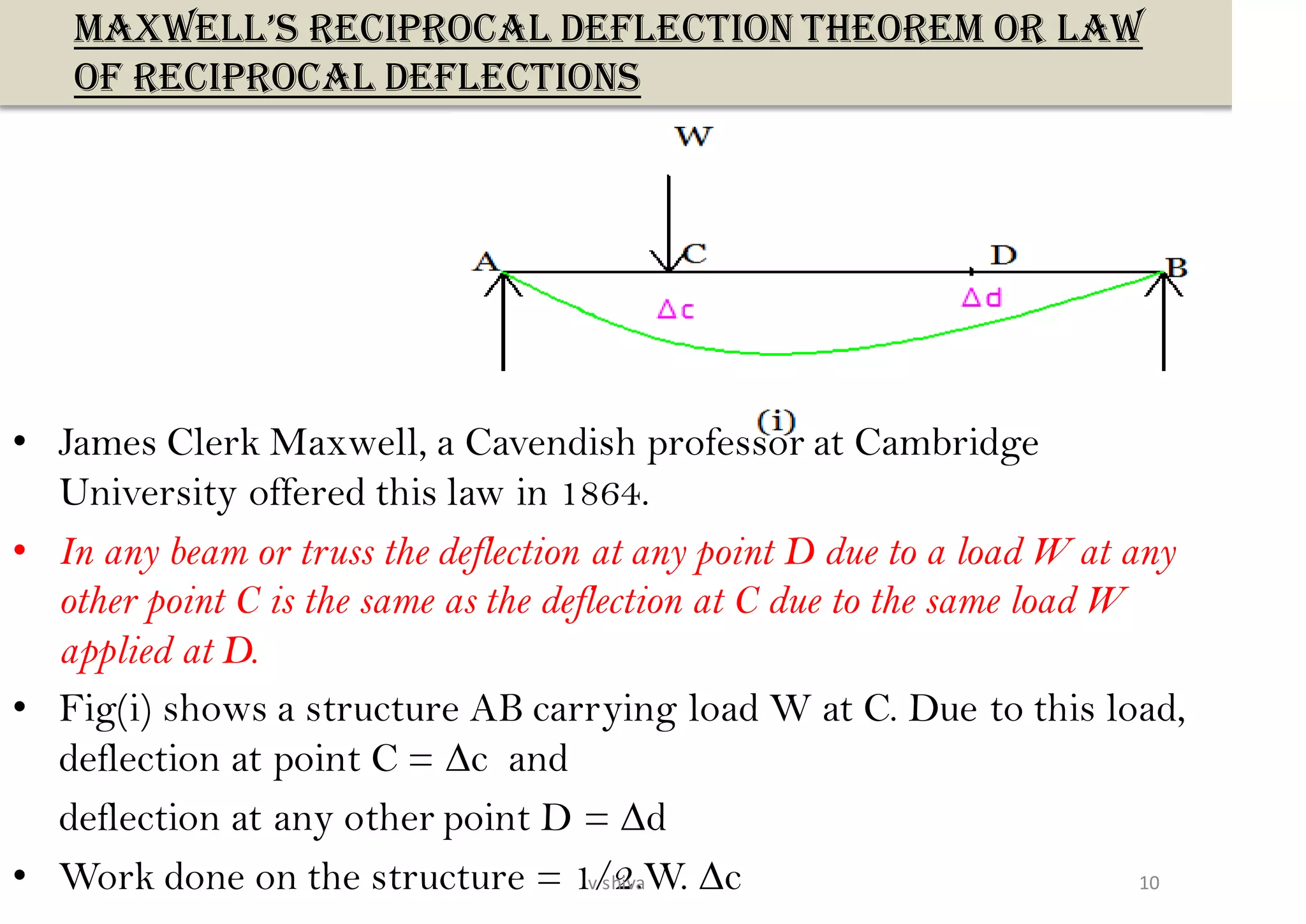
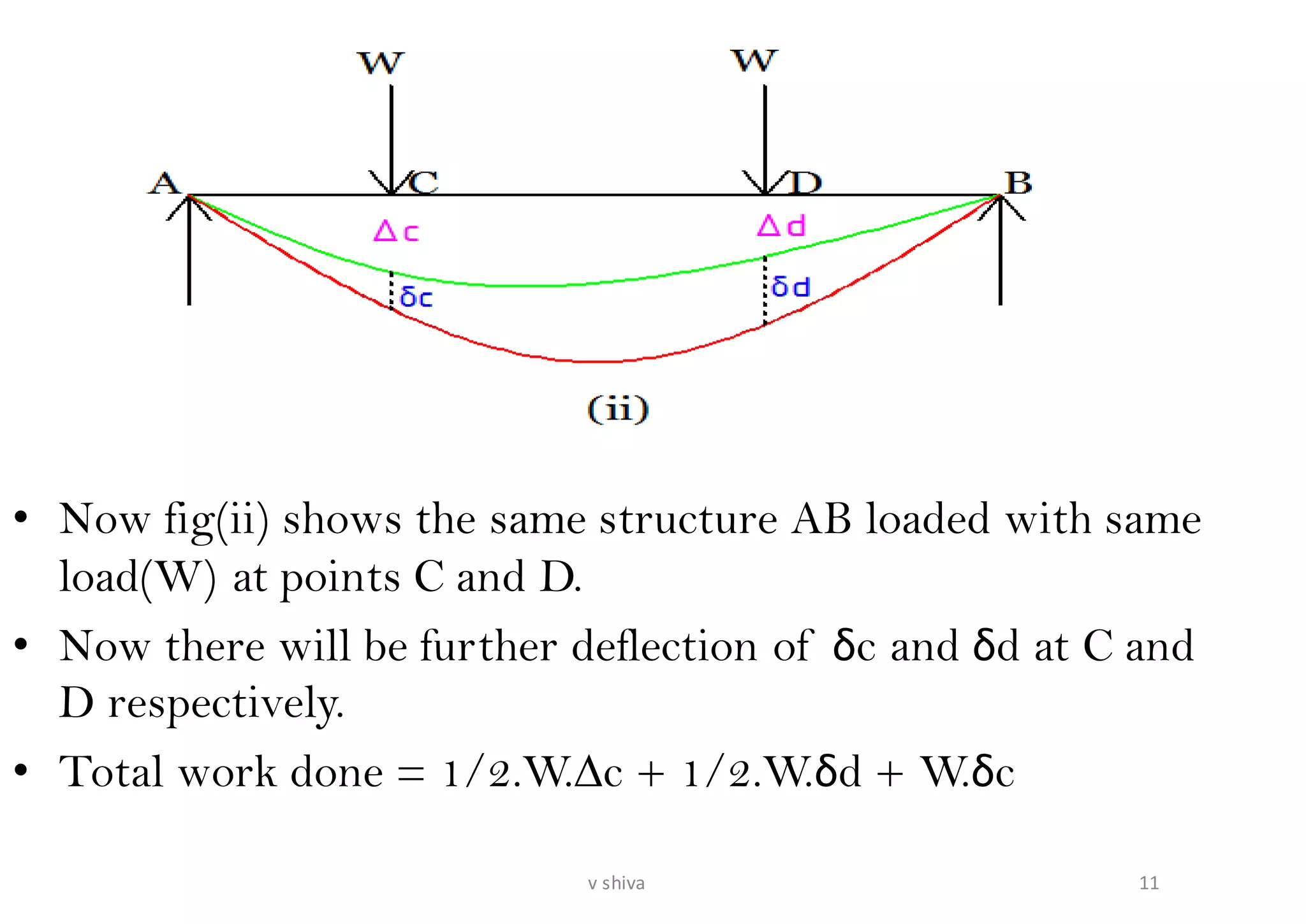
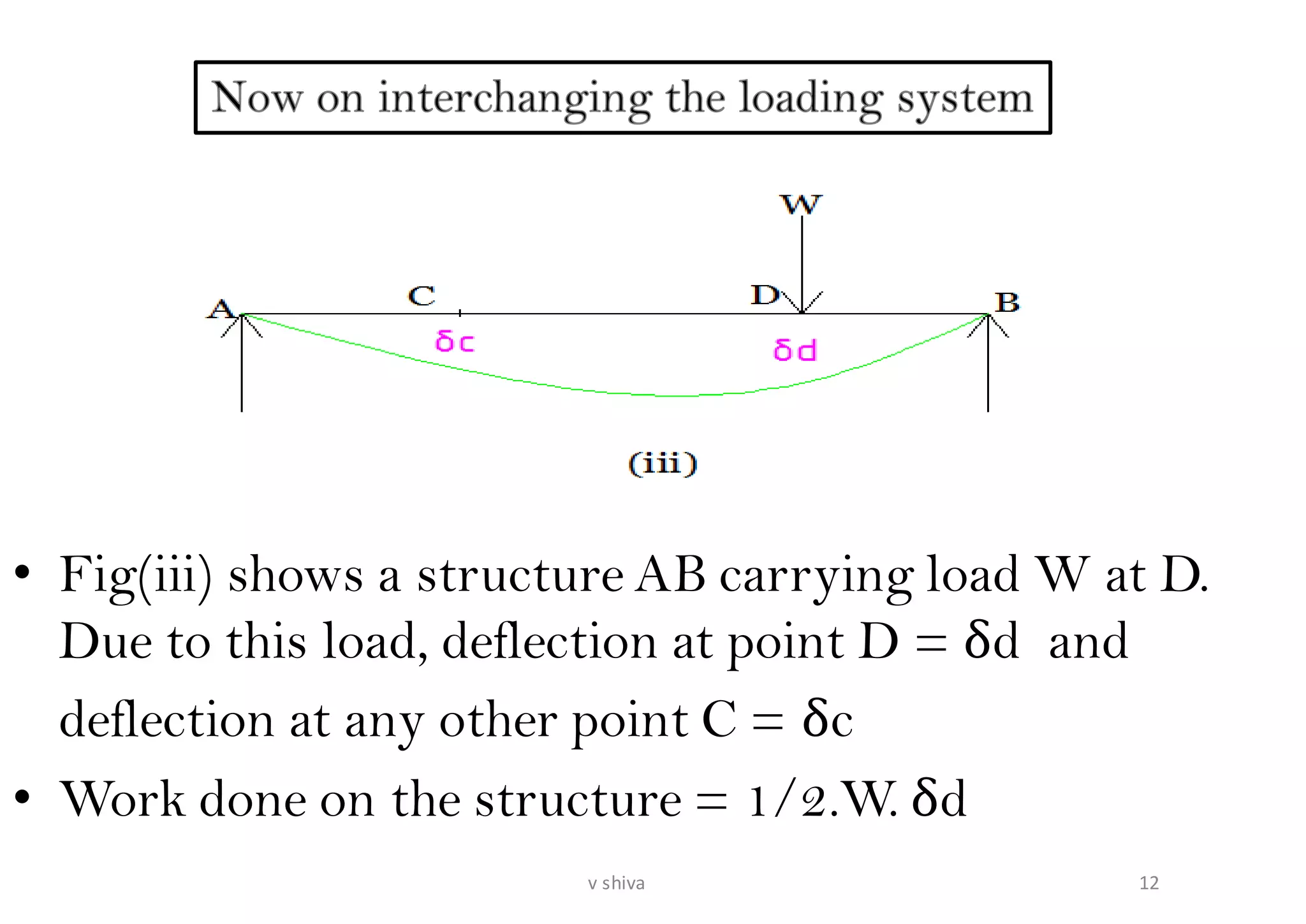
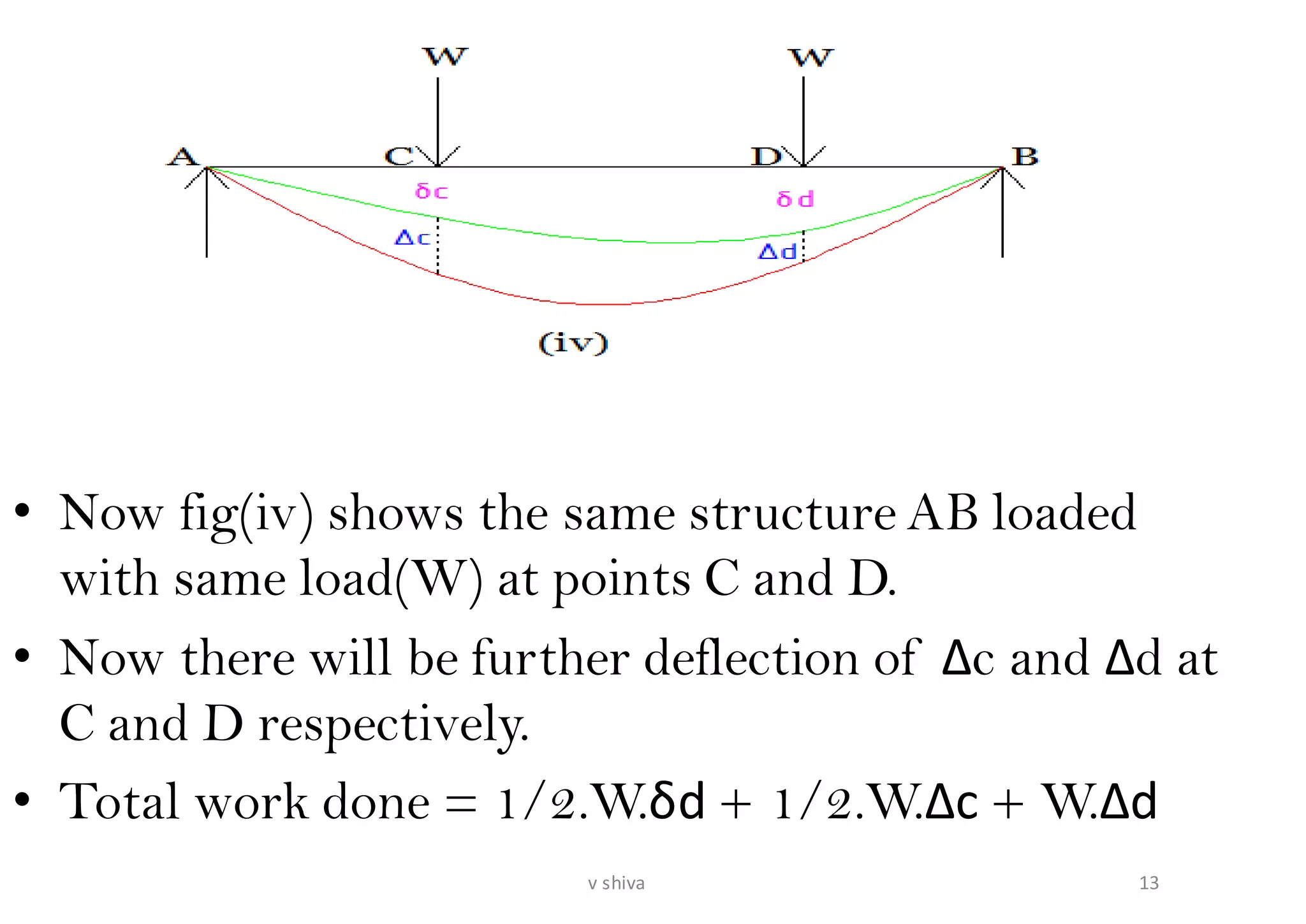
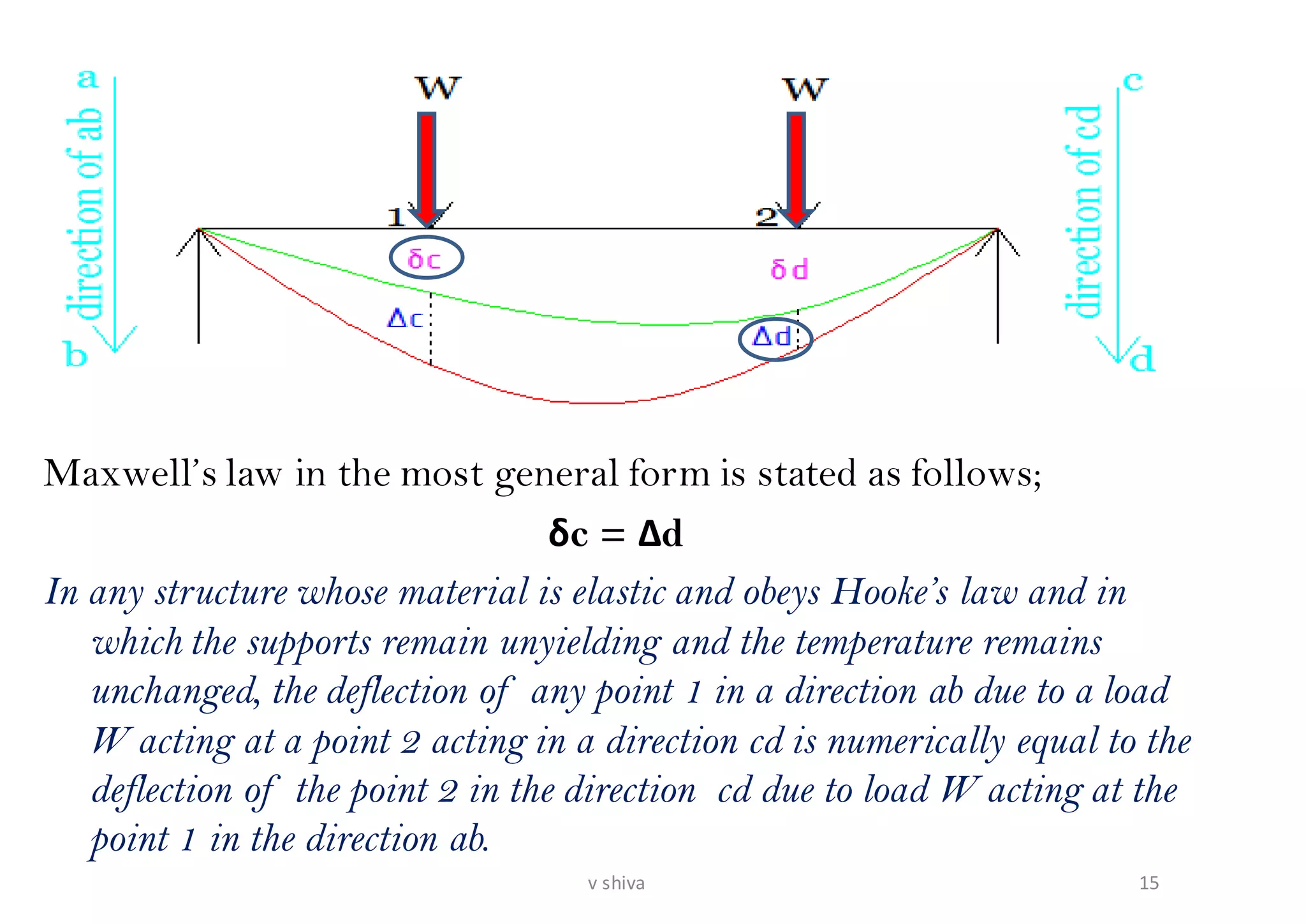
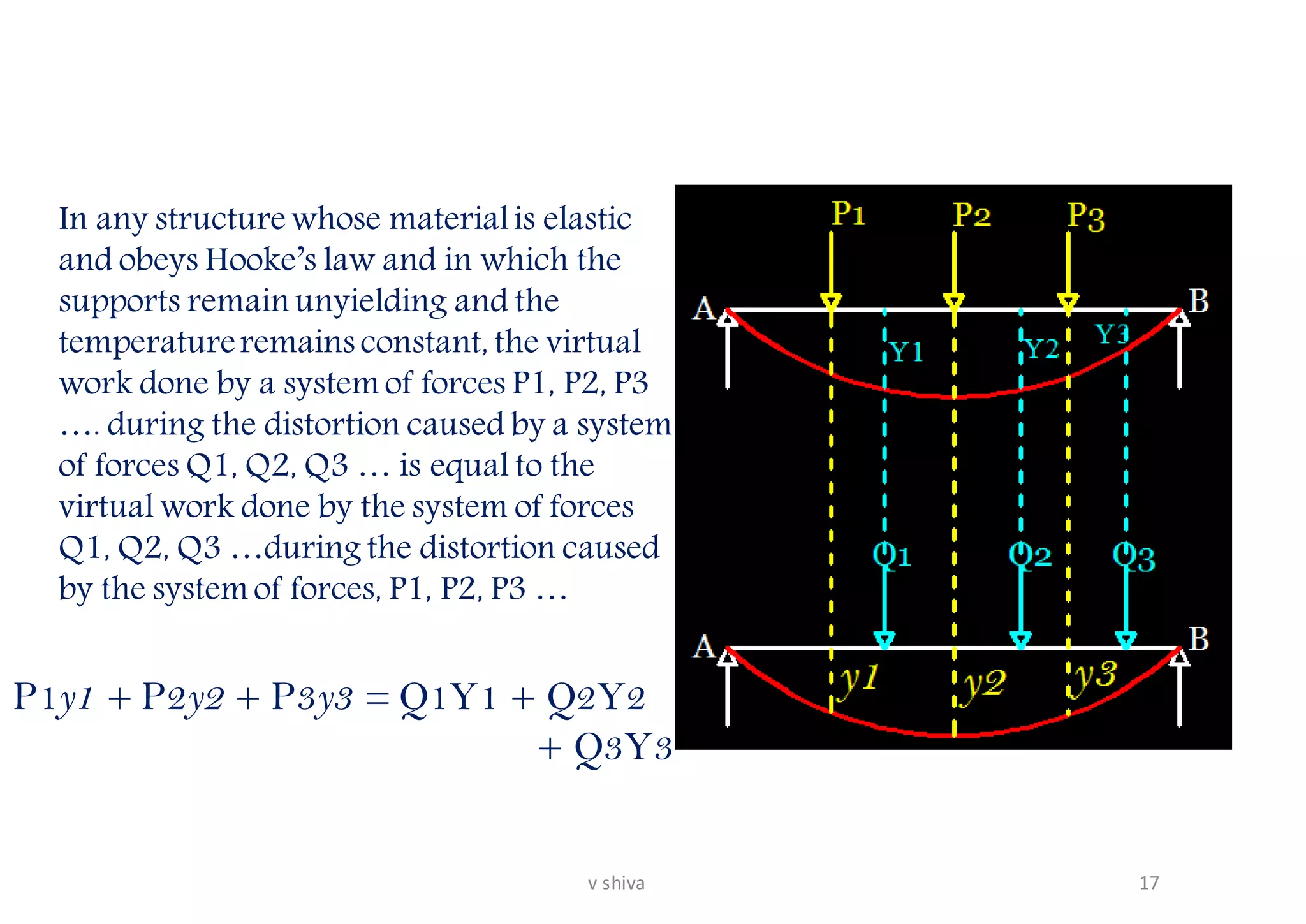
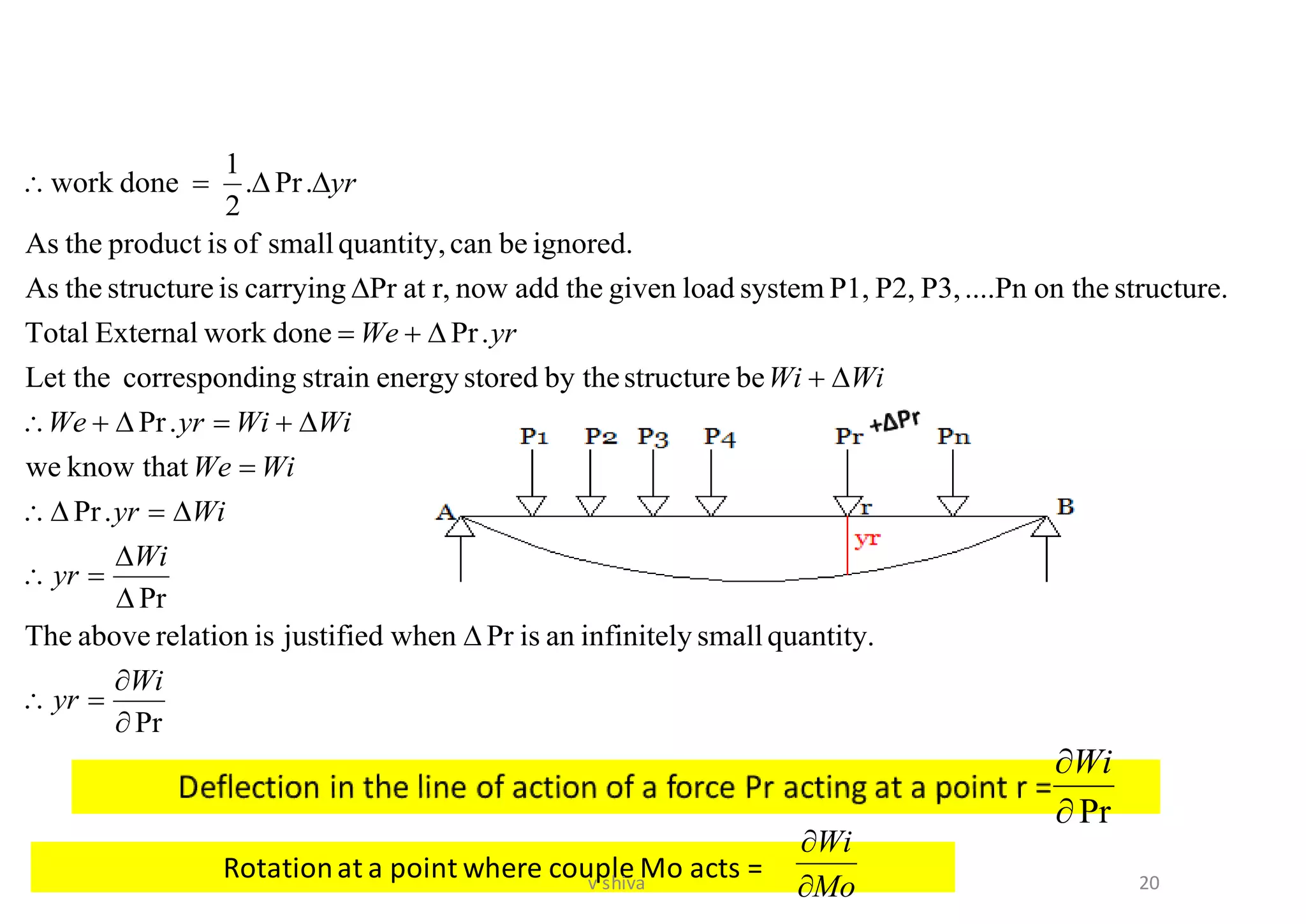
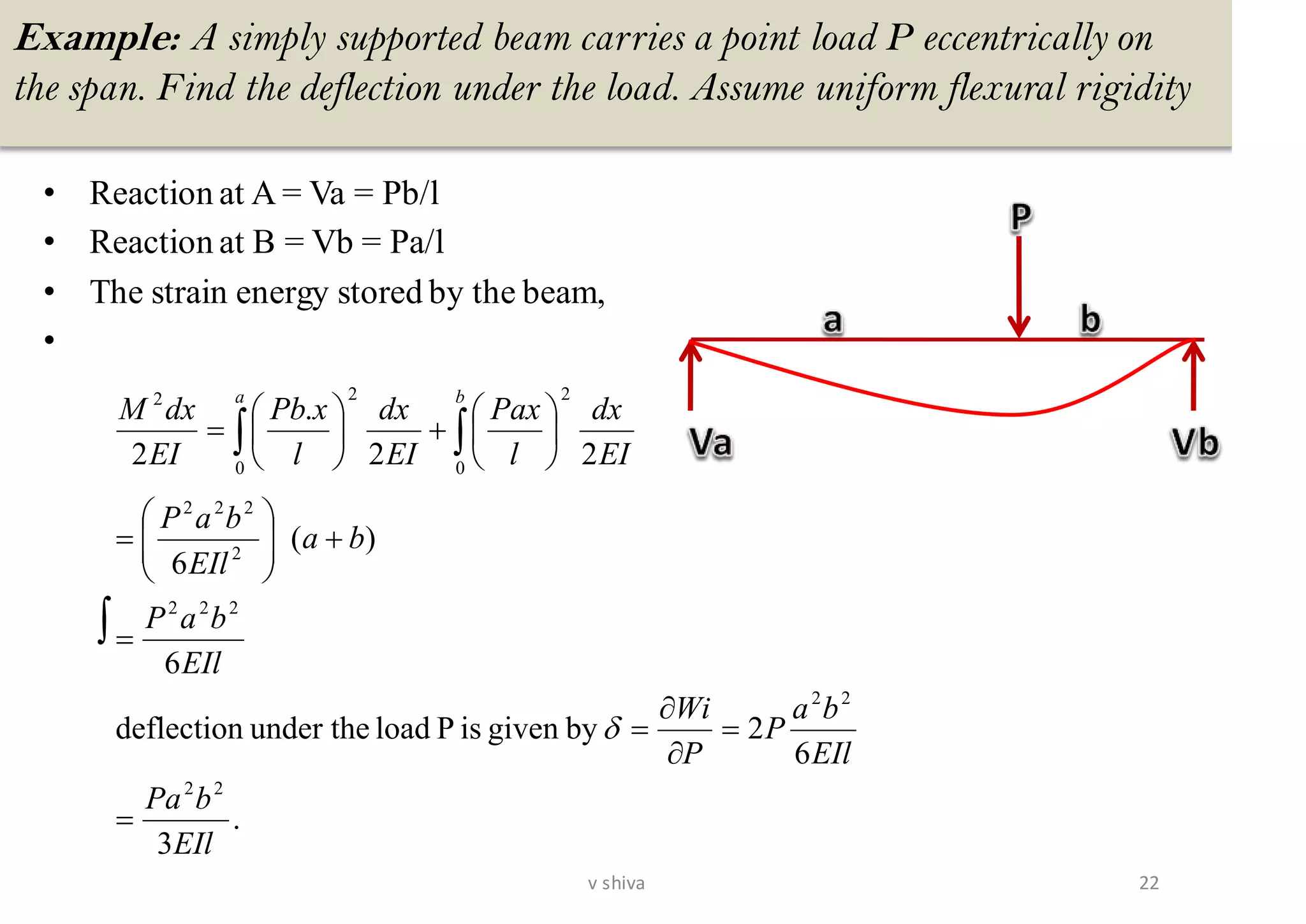
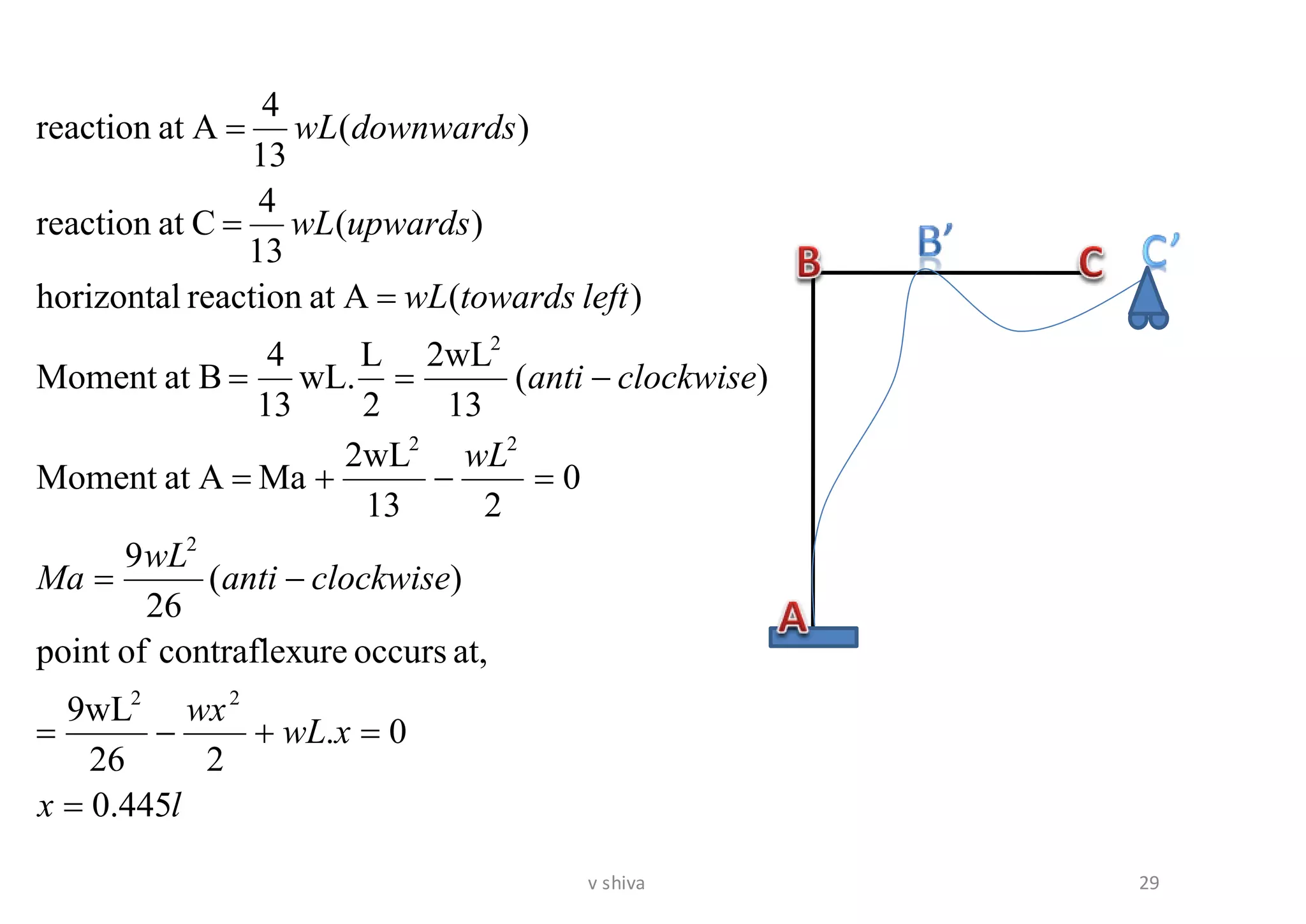
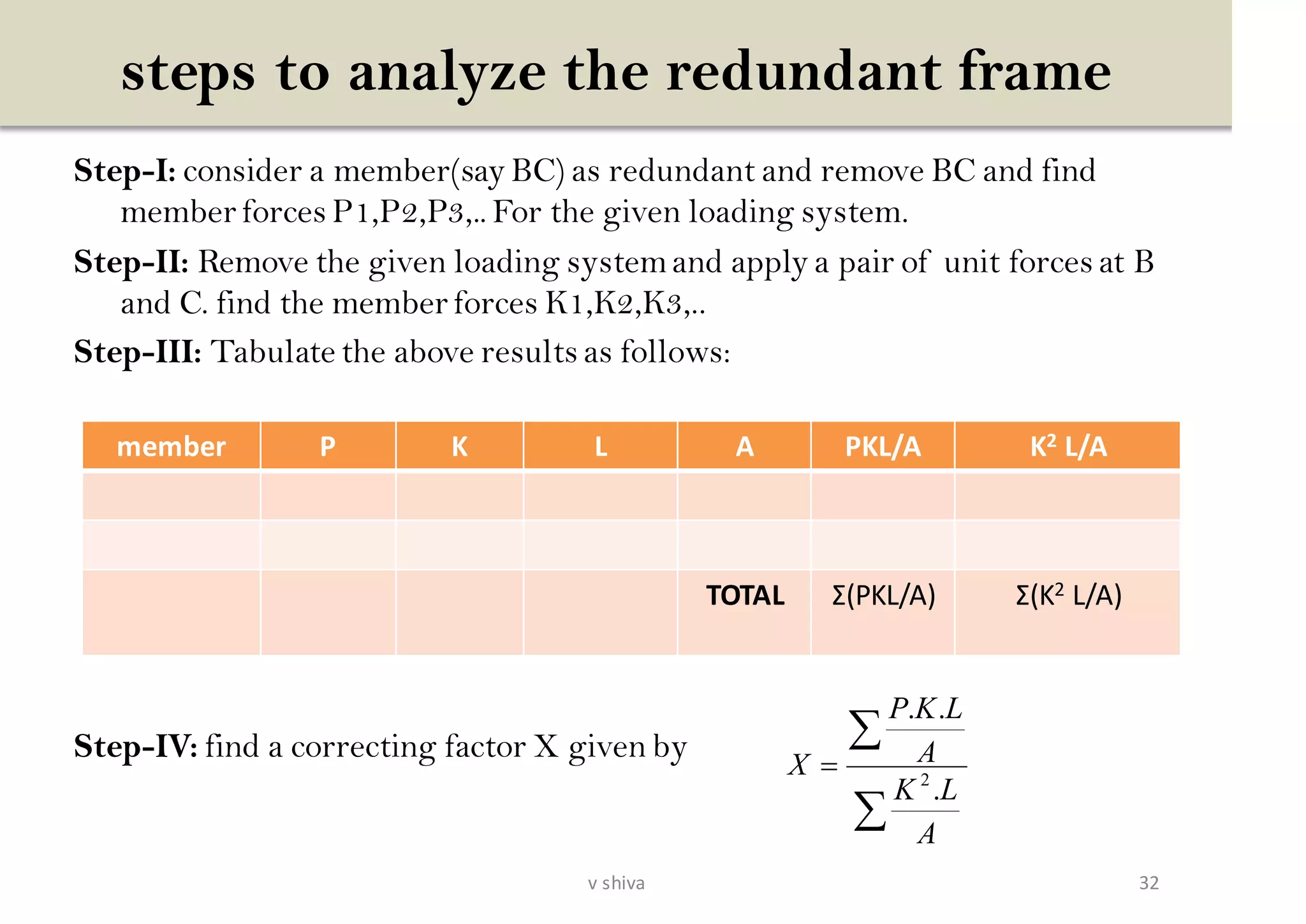
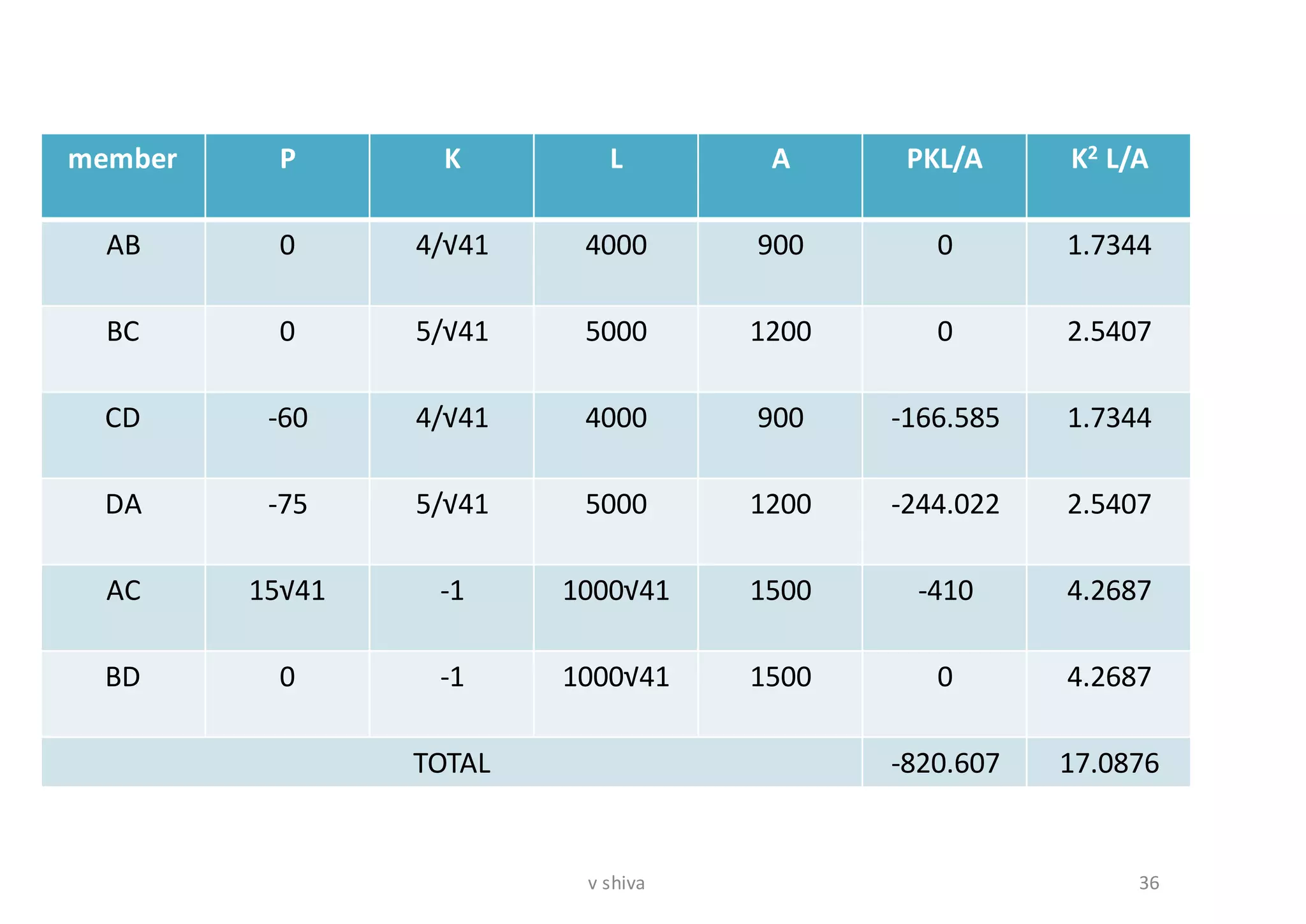
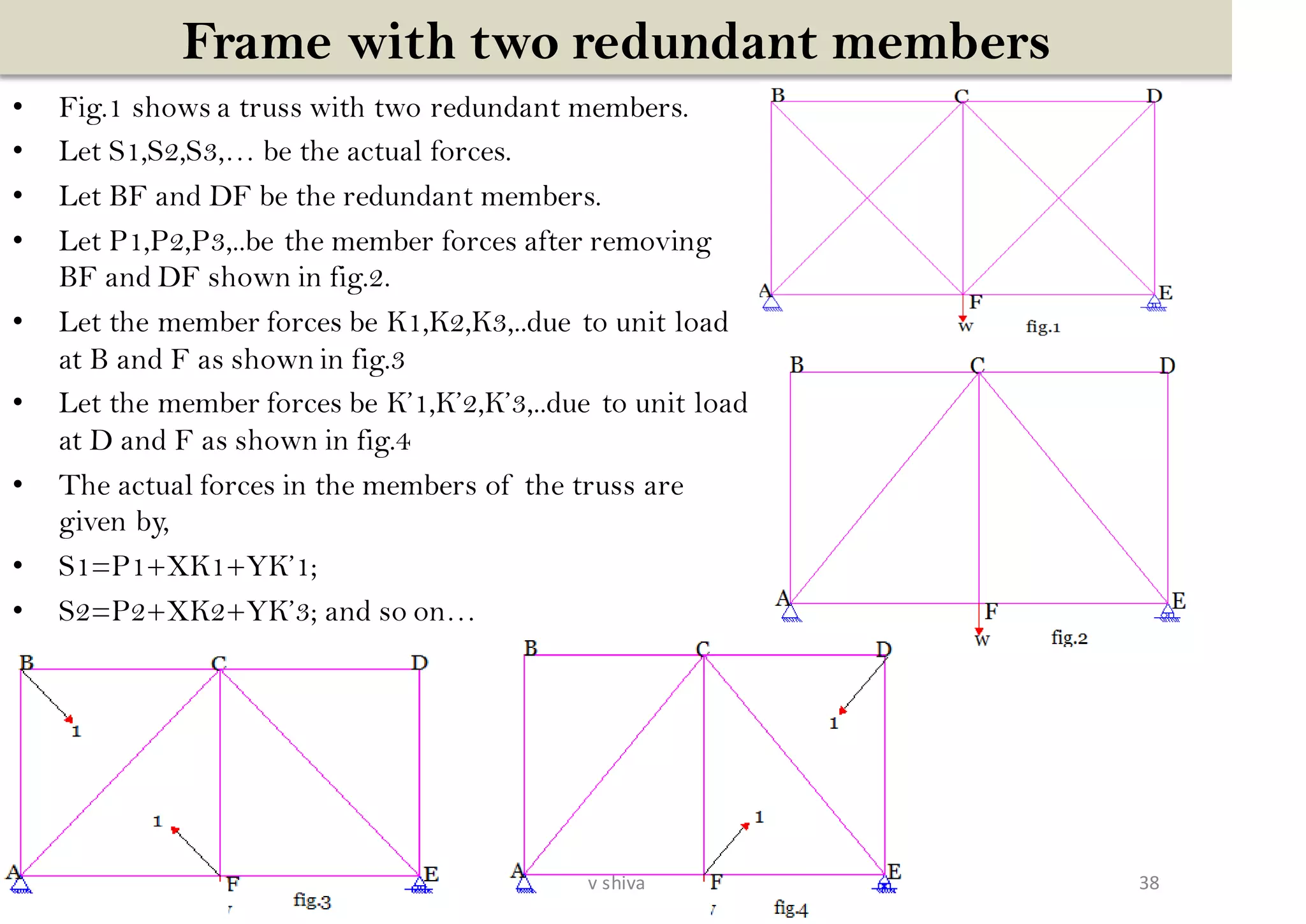
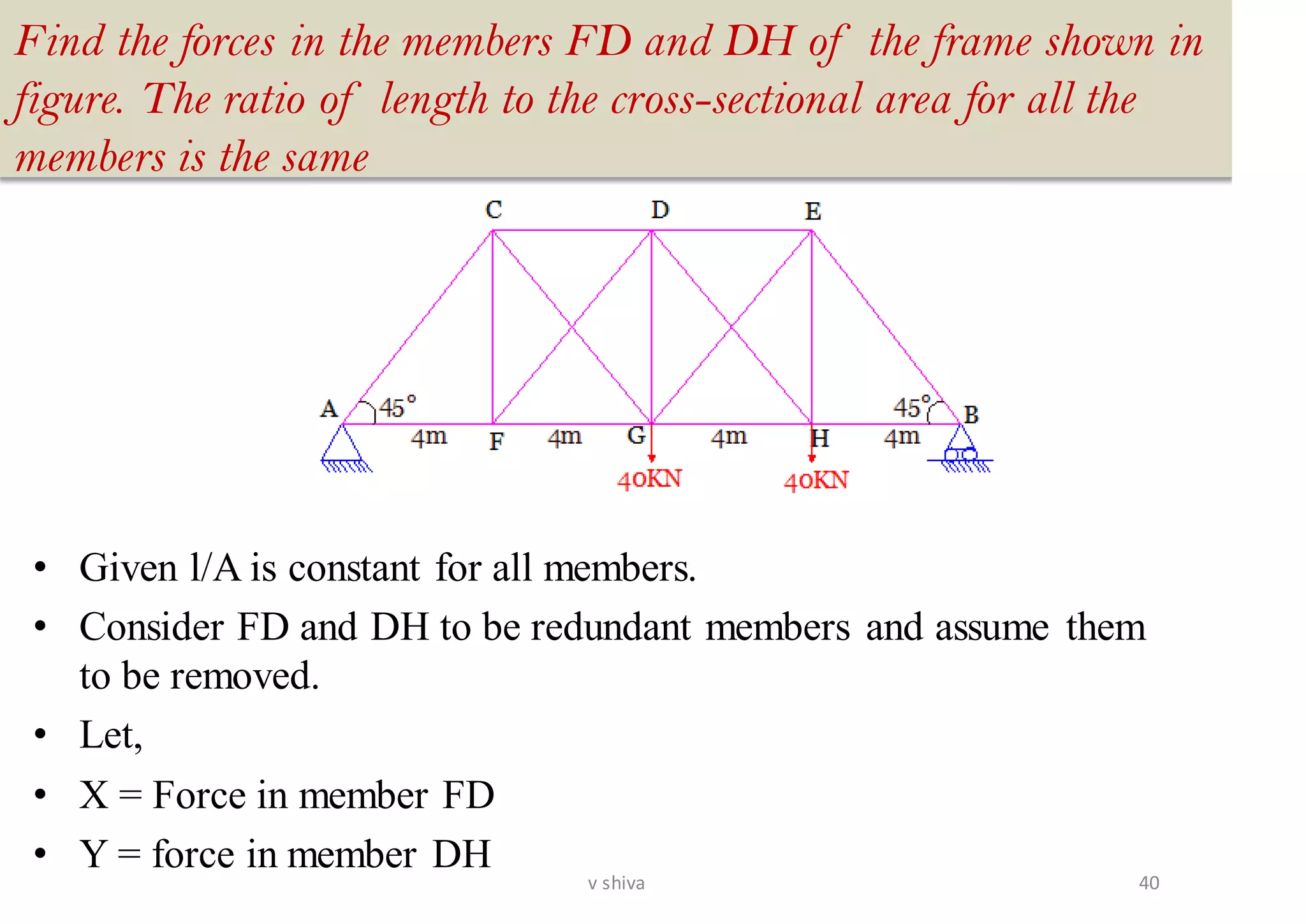
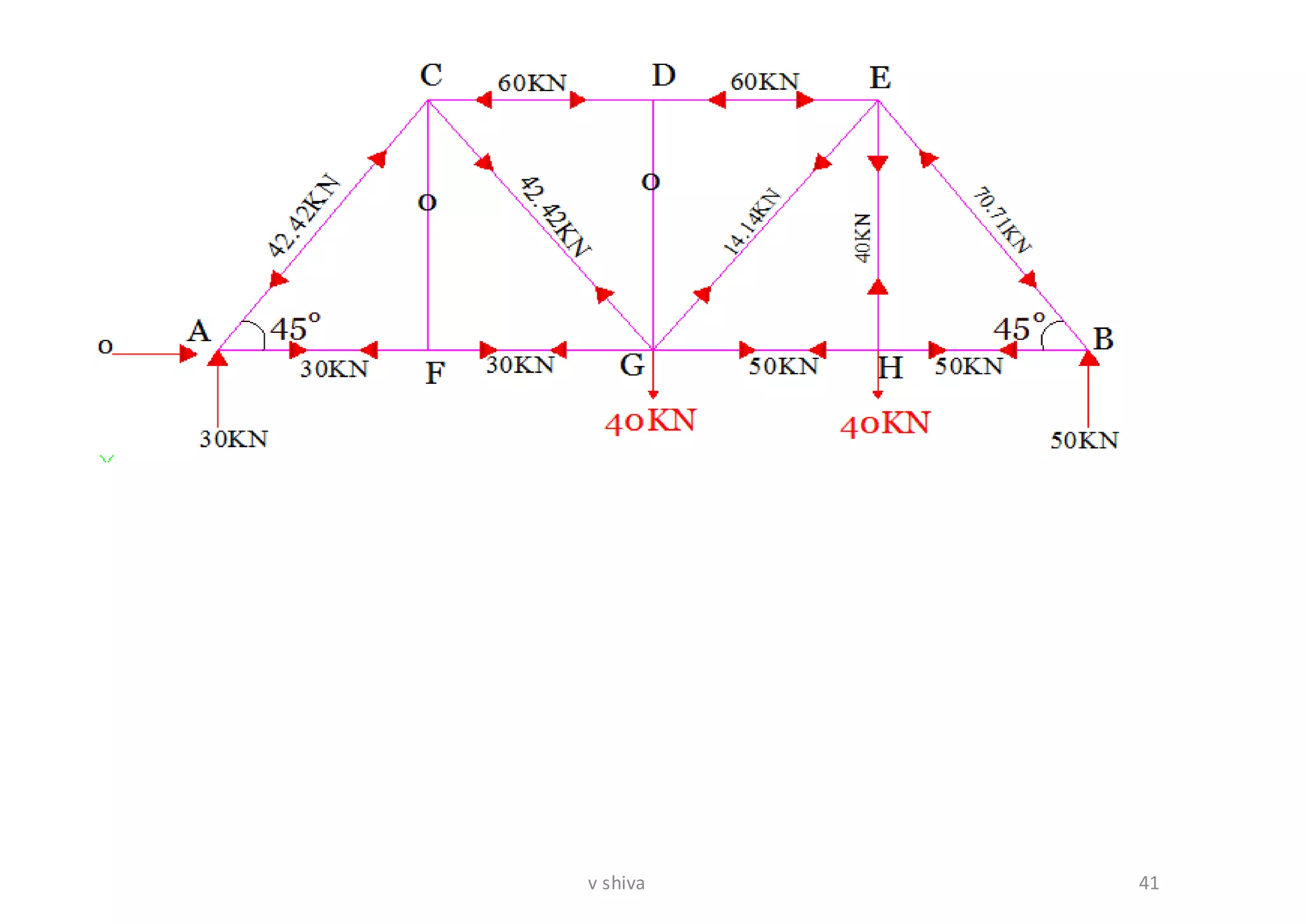
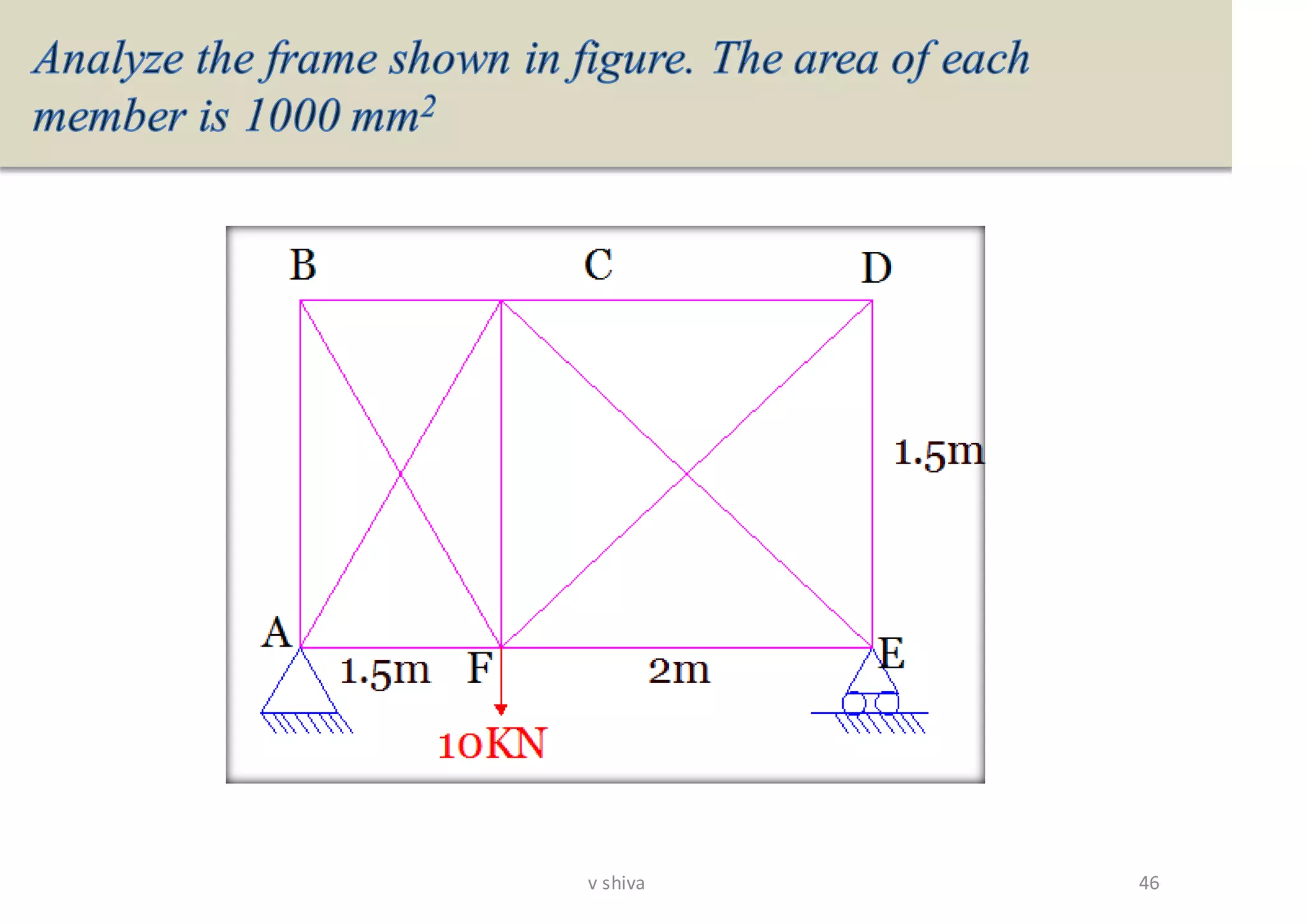
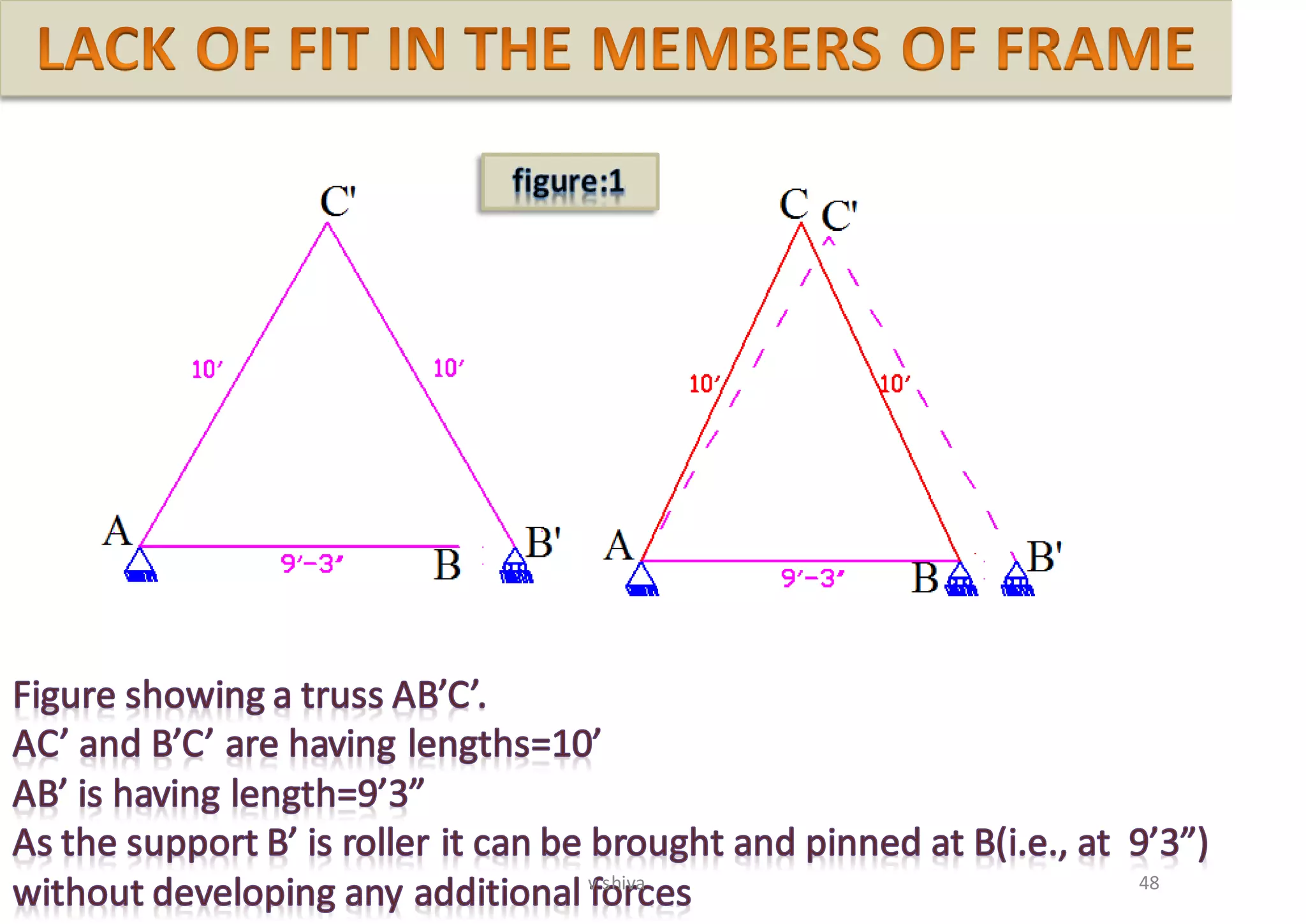
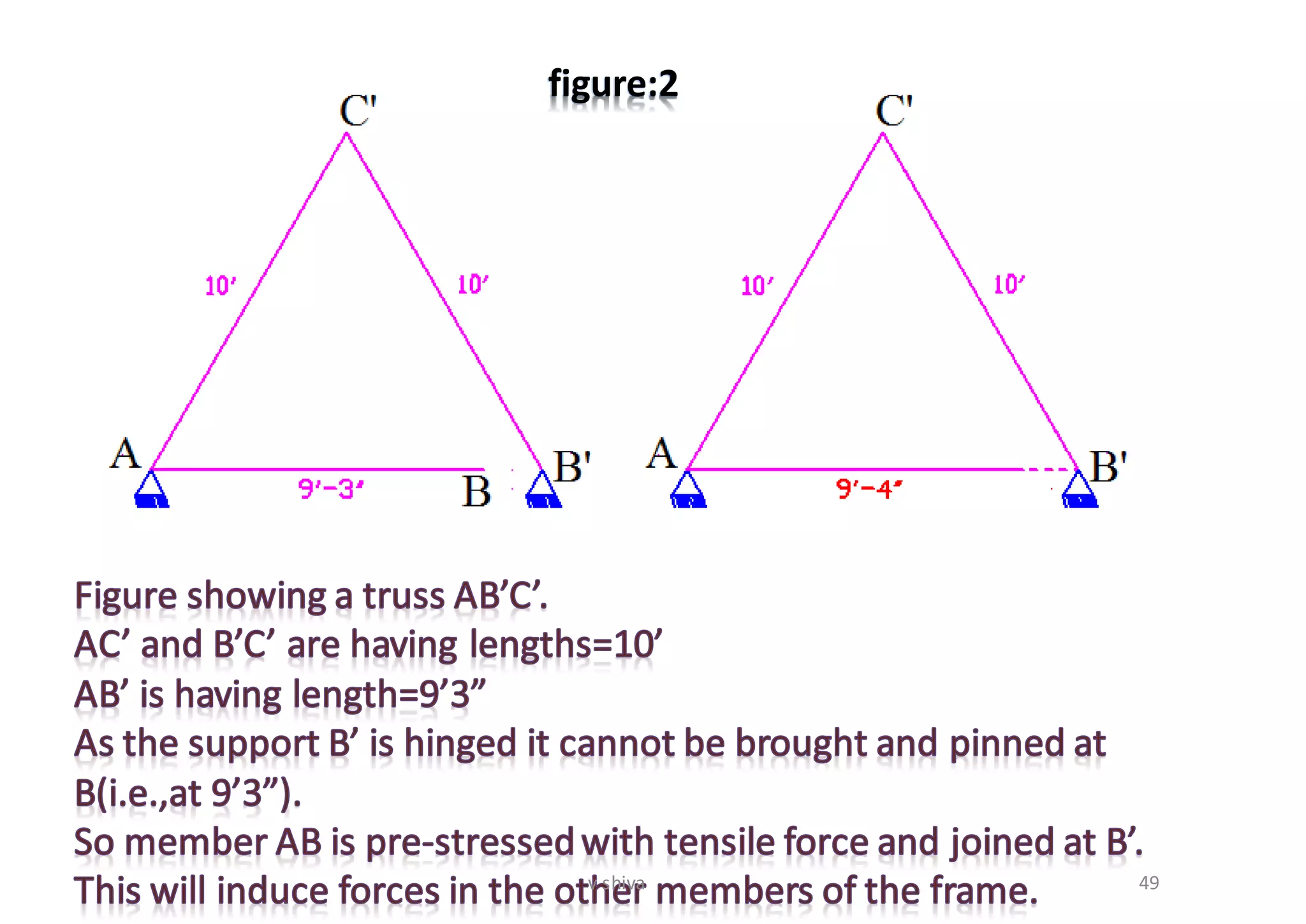
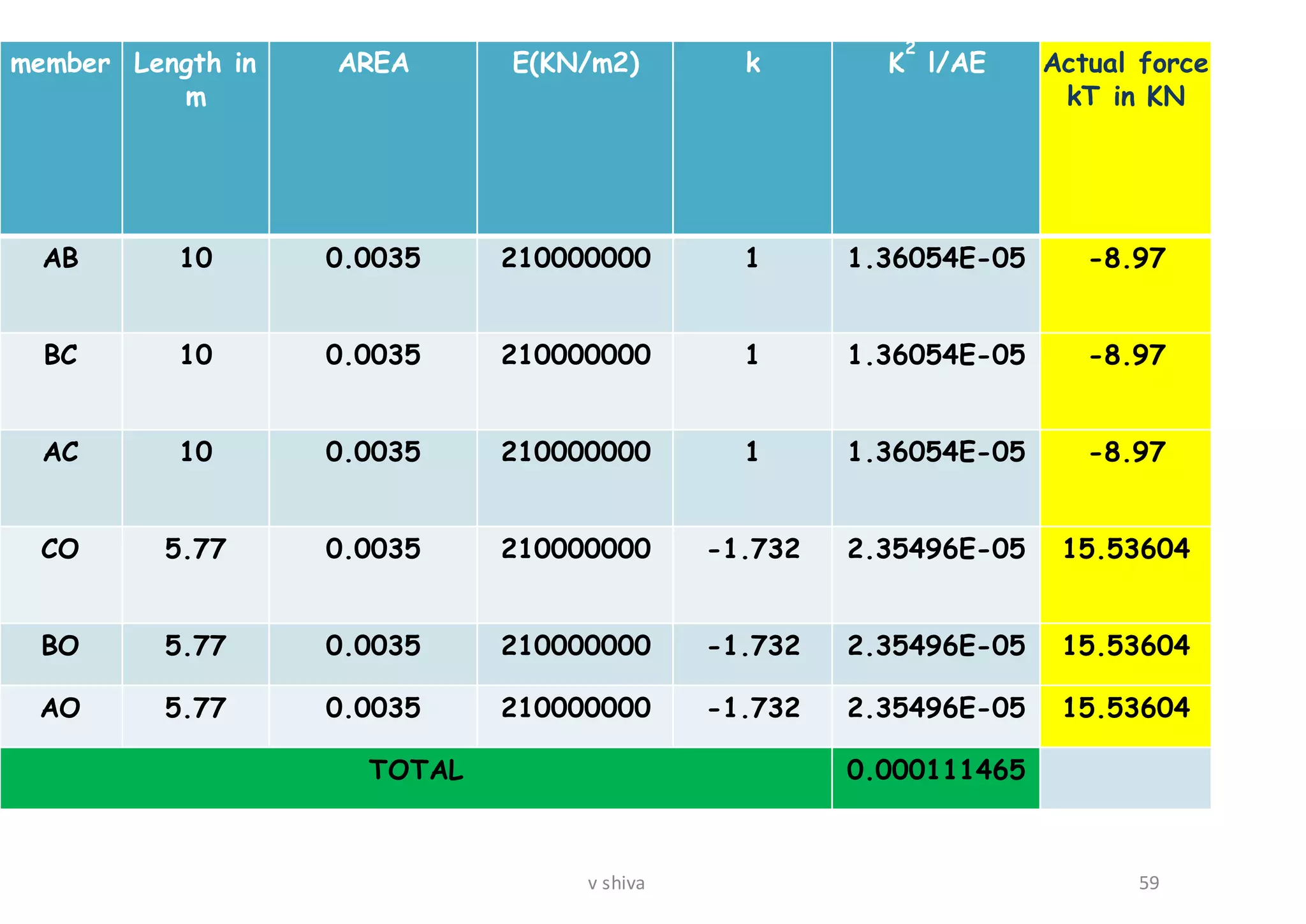
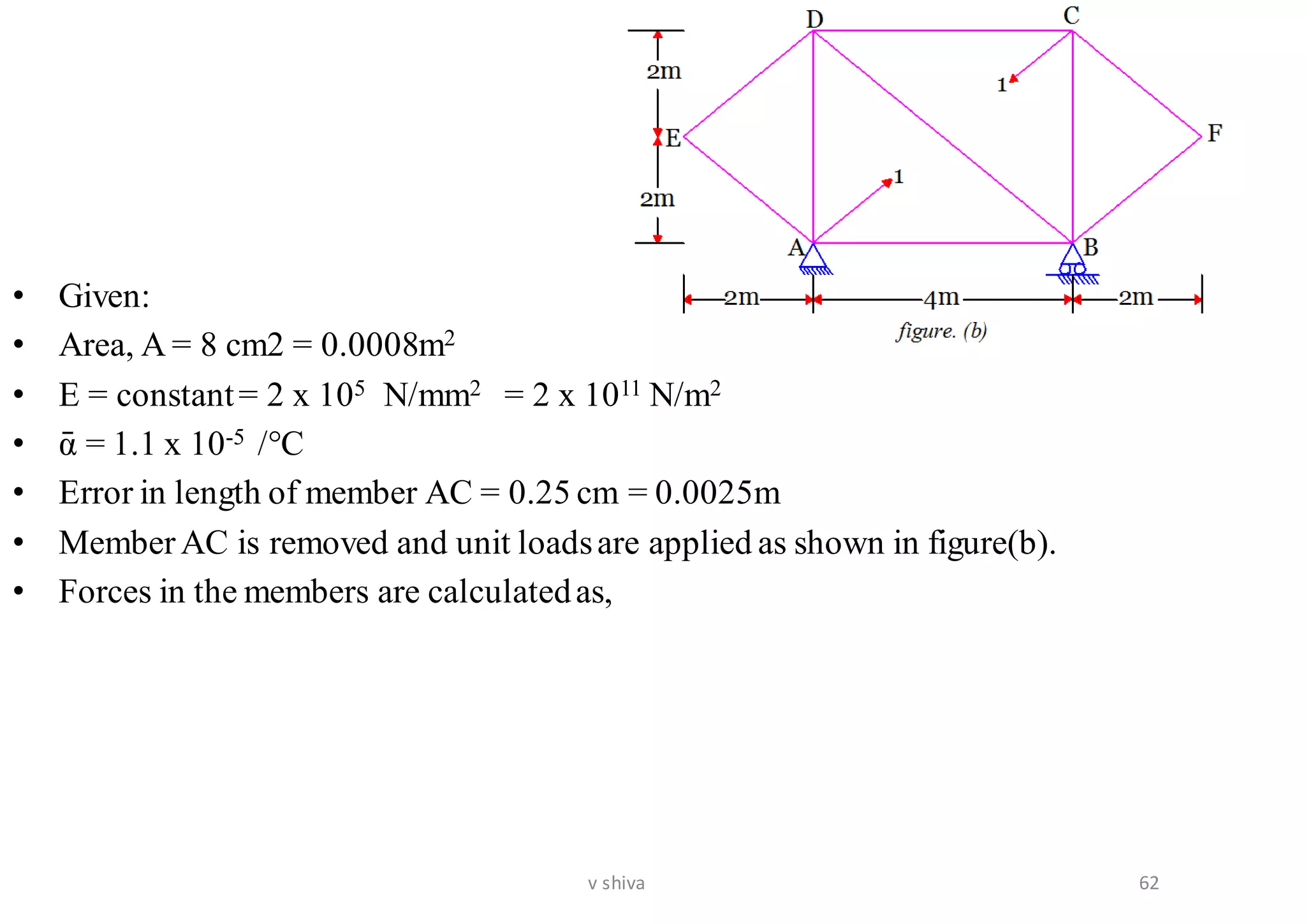
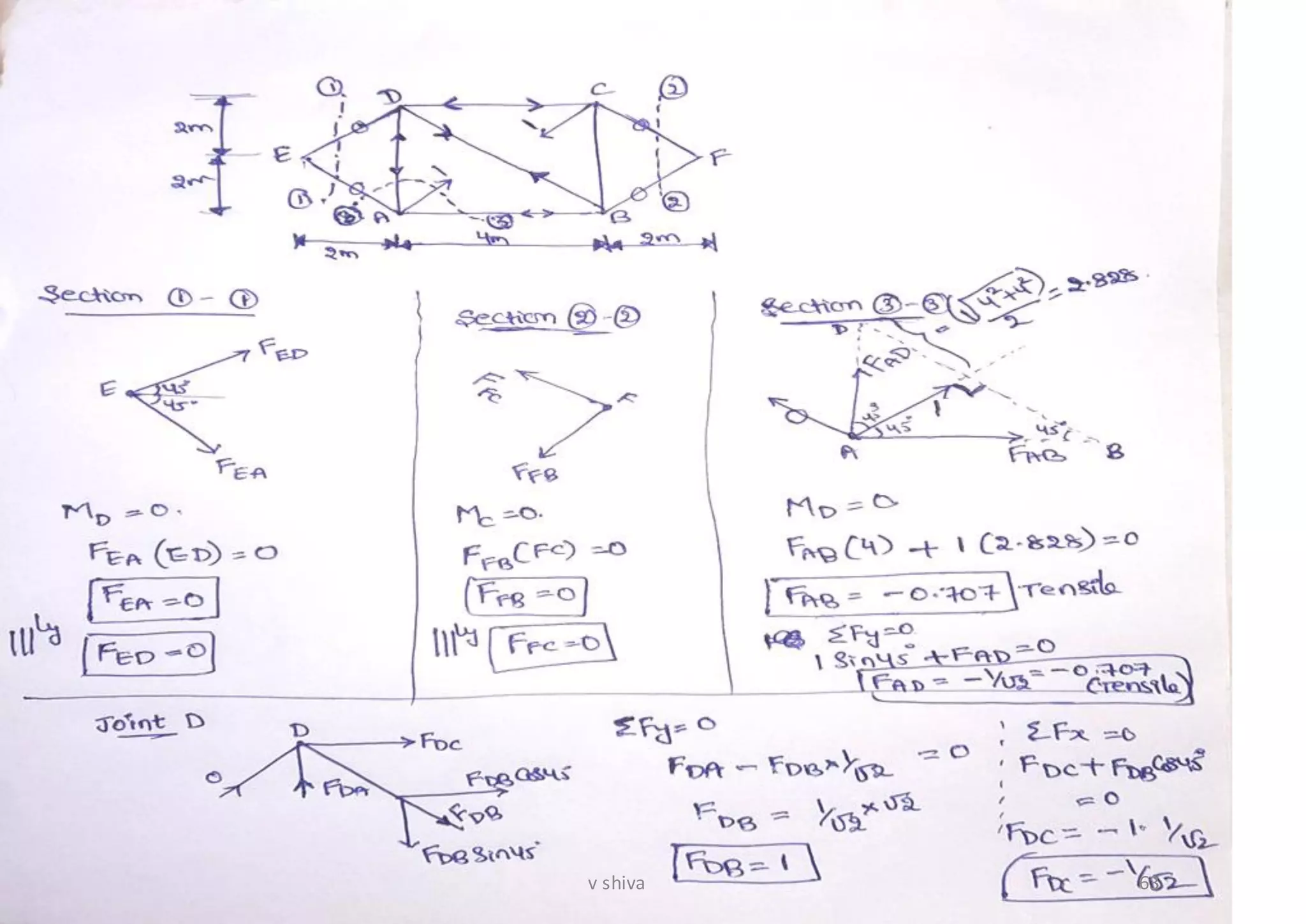
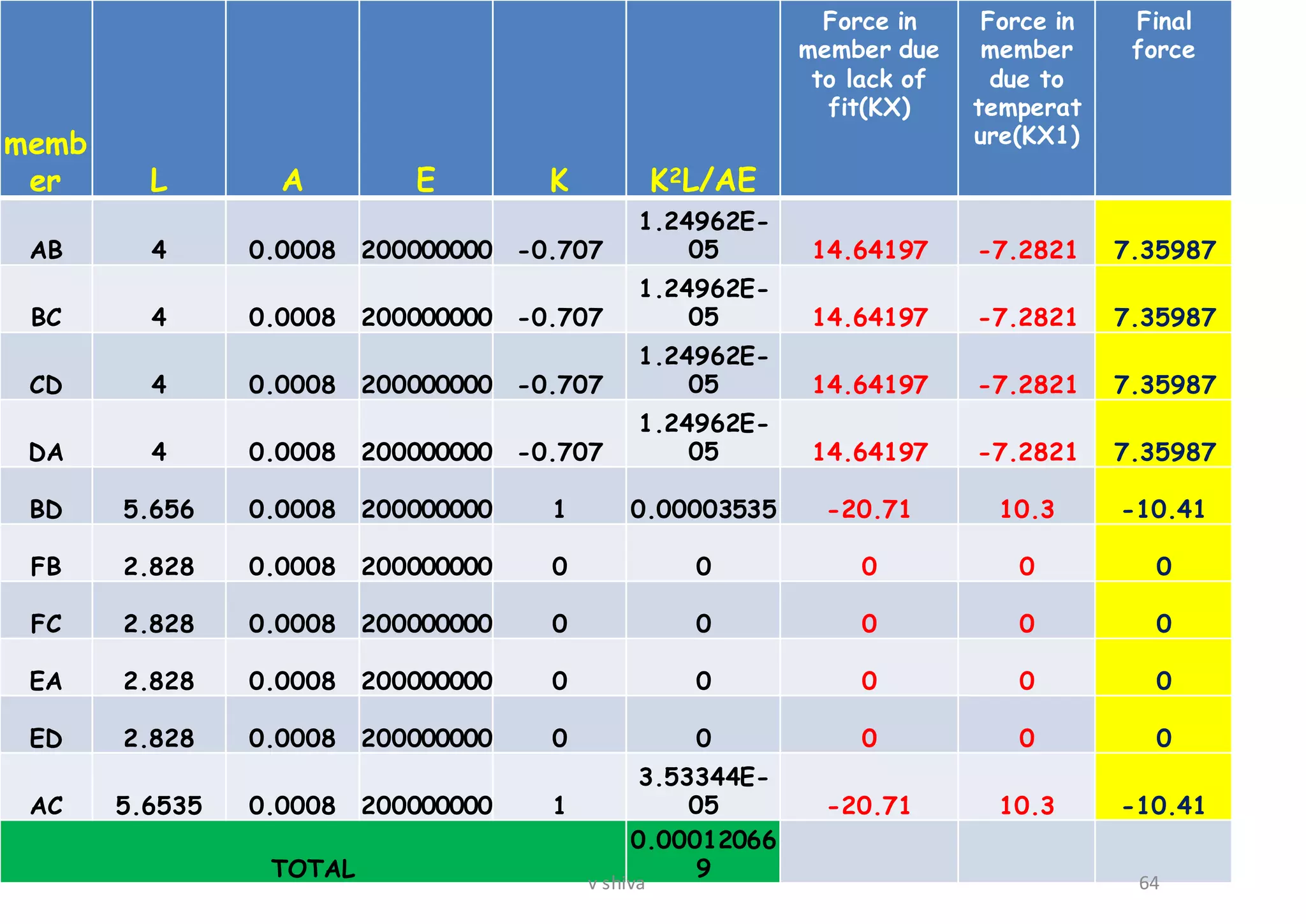
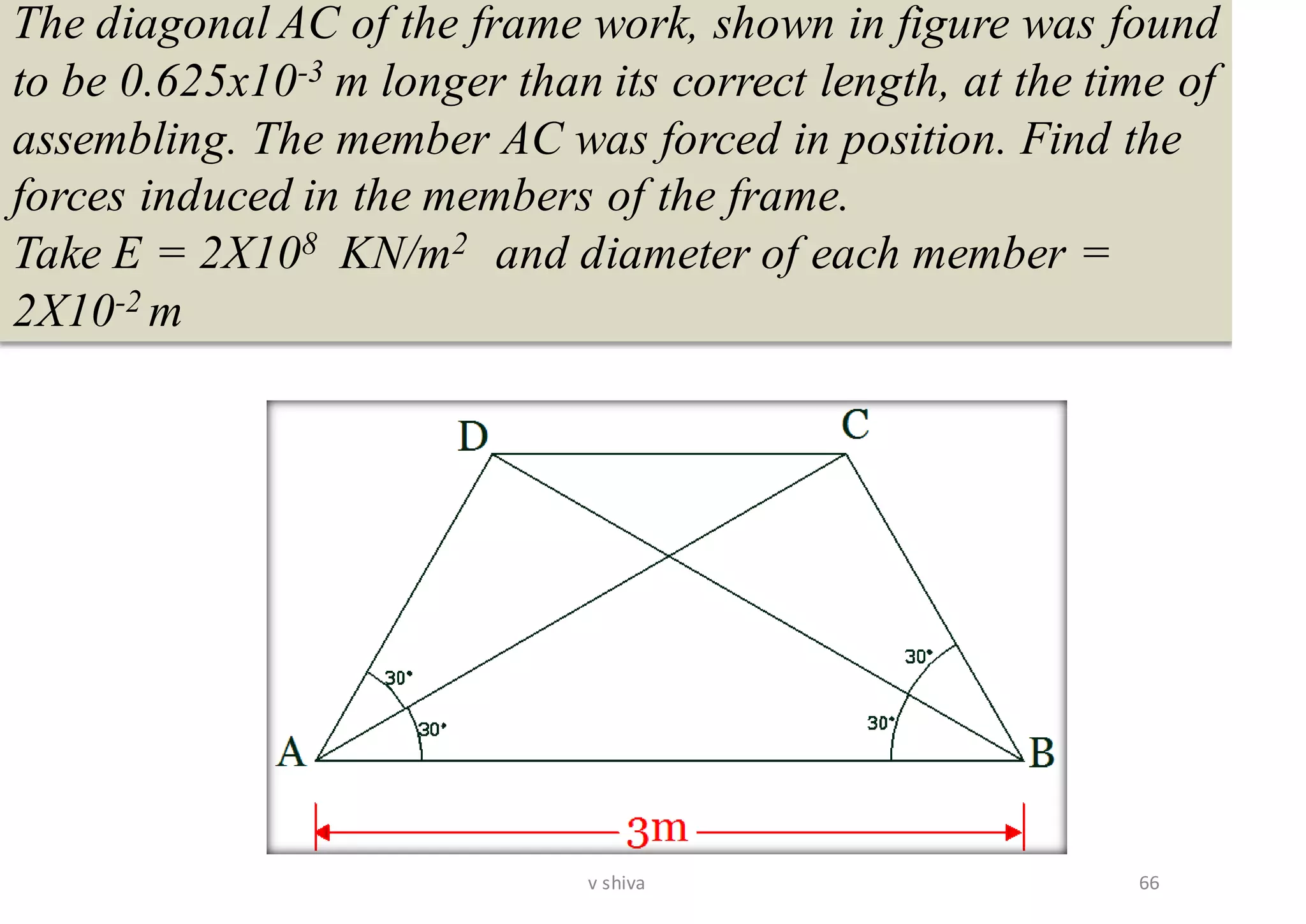
The document discusses strain energy in elastic members, detailing the concepts of work done, stored energy due to axial forces and bending, and theorems such as Maxwell's reciprocal deflection theorem and Castigliano's theorems. It covers calculations for deflections in various beam configurations under loading and provides a theoretical foundation for analyzing indeterminate structures related to strain energy. Additionally, it emphasizes the relationships between external work, internal strain energy, and structural deflections.