The document discusses various algorithms for finding shortest paths in graphs, such as Bellman-Ford and Dijkstra’s, and their application in network flow analysis. It details calculations for max-min fair flow distribution, capacity constraints, signal processing in GSM networks, and data rates in optical communication systems like SDH/SONET. Additionally, it covers the implications of fiber span analysis on network viability and optimal routing scenarios involving multiple traffic flows.

1. SPST
Floyd-Warshall, Bellman-Ford, Dijkstra’s
Dij = min (wij, Dik + Dkj), Di = min (Di, wik + Dk)
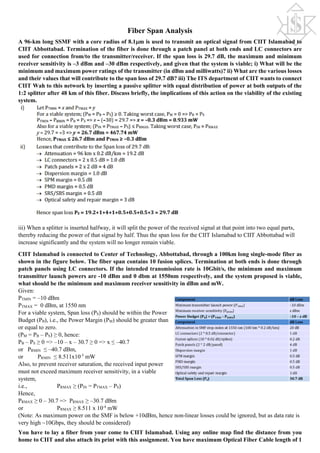
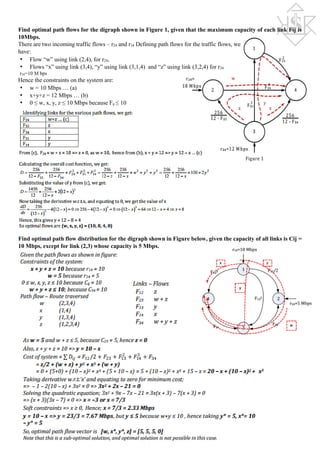
Find and draw the shortest path spanning tree (SPST) for the digraph shown in the figure using the Bellman-
Ford algorithm, from all nodes to node C. Then apply the MaxMin Fair flow control algorithm to find the max-
min fair flow vector for all sessions (shown in red). Assume the capacity of all links to be 10 Gbps. (Hint: All flows
take the minimum cost path)
As the shortest path cost has not changed for any node for 2 successive iterations, so we stop here. The SPST is shown
in the Figure.
All flows cause overflow on link EC, hence all flows stopped at 2.5 Gbps Max-min fair flow distribution is: [rAC, rDC,
rBC, rEC] = [2.5, 2.5, 2.5, 2.5]
Find the shortest path from all nodes to node 1 for the digraph shown in Figure 2, using the BellmanFord
algorithm. b.) Draw the SPST for node 1 as found in part (a).

2. Find the shortest path for all origin-destination pairs in Figure 4 using an appropriate technique.

3. For the network given below, find the SPST with ‘B’ as the node of interest using Bellman-Ford’s method. Show
all intermediate steps. Also draw the SPST. b) If each node has exactly one flow to node ‘B’ and that flow takes
the shortest path to node ‘B’, find the max-min fair flow vector for all flows. It is given that the capacity of link
DA is 1 Mbps, while all other links are 4 Mbps.
For more:
file:///E:/Telecommunication%20Systems%20Engineering/assignments/Solution_Problem%20Set%202_Routing.pdf
file:///E:/Telecommunication%20Systems%20Engineering/assignments/Q2-A-soln.pdf
file:///E:/Telecommunication%20Systems%20Engineering/assignments/Q2-B-soln.pdf

4. MST
Kruskal’s algorithm, Prim-Dijkstra’s algorithm
Operation of Kruskal's algorithm Prim-Dijkstra’s algorithm
Find the MST and the cost of the MST for the graph shown in Figure 1, using Prim Dijkstra’s method. Use node
3 as the starting node.
Find the MST of the graph shown in Figure 3 using Kruskal’s algorithm? Show your steps.

5. GSM
Question: (a) Indicate the GSM network elements which are responsible for executing these tasks
(i) Frequency hopping (ii) Rate adaptation (iii) Encryption and decryption (iv) Authentication.
(a) (i) BTS and BSC (ii) BTS (iii) BTS and BSC (iv) BSC
(b)How can discontinuous transmission and reception contribute towards optimizing the performance of a mobile
communication system from a user's and network's perspective?
(c) In GSM frame hierarchy, the periodic pattern of 26 slots occurs in all TDMA frames for a traffic channel.
What is the total time elapsed for 26 time slots when each slot is of 4.615 ms duration? 24 out of 26 time slots are
dedicated for user data transmission and each normal burst for data transmission carries 114 bits of user data.
Compute the maximum data rate.
Total time for 26 time slots= 26x4.615 =120 ms. Total number of bits carried in 26 slots= 114 bits/slot x 24
slots/multiframe =2736 bits (as 24 slots dedicated for user data transmission) Maximum data rate= (114 bits/slot) * (24
slots/multiframe) / (120 ms/mutiframe) = 22.8 Kbps
Indicate the functions of flag bit, guard bits and train bits in GSM frames.
Solution: (a) FLAG bit indicates whether user information or control information GUARD bits reduce interference to
signals in nearby cells using the same carrier. During this period no data is sent. It is at the end of the burst. TRAIN
(Training sequence) bits select the strongest signal in case of Multipath propagation
(b) For the registration procedure of a mobile station in a new MSC area would location update and authentication
confirmation involve the BSC and MSC of that area? Give reasons.
In case of registration in a new location BTS would report to BSC and onward to MSC about location change aspect and
mobility management thus authenticating the mobile station in that area so that it would be updated in the record of VLR.
(c) Discuss the conditions due to which handovers are initiated in a system and what are the types of handover?
The handovers are initiated due to signal strength deterioration at the edge of a cell and to establish communication with
the new cell tower thus also managing Traffic and load balancing (to ease traffic congestion). There are two types: Hard
handover and Soft handover.
Optimal Routing
Find optimal path flows for the digraph shown in Figure 1, given that the maximum capacity of each link Fij is
10Mbps.
There are two incoming traffic flows – r24 and r34 Defining path flows for the traffic flows,
we have: • Flow “w” using link (2,4), for r24, and “z” using link (3,2,4) for r34
Hence the constraints on the system are:
• w = 10 Mbps … (a)
• x + y + z = 12 Mbps … (b)
• 0 ≤ w, x, y, z ≤ 10 Mbps because Fij ≤ 10
Identifying links for the various path flows, we get
From (c), F24 = w + z = 10 => z = 0, as w = 10, hence from (b), x + y = 12 => y = 12 – x … (c)
Calculating the overall cost function, we get:

6. Find optimal path flows for the digraph shown in Figure 1, given that the maximum capacity of each link Fij is
10Mbps.
There are two incoming traffic flows – r24 and r34 Defining path flows for the traffic flows, we
have:
• Flow “w” using link (2,4), for r24,
• Flows “x” using link (3,4), “y” using link (3,1,4) and “z” using link (3,2,4) for r34
r24=10 M bps
Hence the constraints on the system are:
• w = 10 Mbps … (a)
• x+y+z = 12 Mbps … (b)
• 0 ≤ w, x, y, z ≤ 10 Mbps because Fij ≤ 10
Find optimal path flow distribution for the digraph shown in Figure below, given the capacity of all links is Cij =
10 Mbps, except for link (2,3) whose capacity is 5 Mbps.

7. Find optimal path flows for the digraph shown in the Fig. below, given the capacity of all links is Cij = 10 Mbps,
except for link (2,3) whose capacity is 5 Mbps.
Let the path flows for r13 be w and x, while the path flows for r23 be y and z as shown
The constraints are as follows:
Solving (10) and (11)
simultaneously results in;
Clearly, this violates the soft
constraint in (1), hence we take;
Thus, our optimal* solution is:

8. Find optimal path flows for the digraph shown in the Fig. below, given the capacity of all links is Cij = 10 Mbps,
except for link (2,3) whose capacity is 8 Mbps
Find the optimal path flow distribution for the digraph shown in Figure 1 below.

9. Link Flow Control
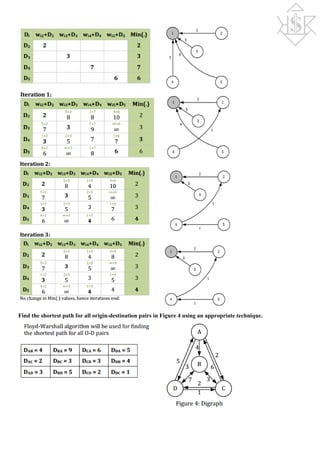
If the cost function is given as 𝐷𝐷𝐷𝐷𝐷𝐷 𝐹𝐹𝐹𝐹𝐹𝐹 = − 𝐹𝐹𝐹𝐹𝐹𝐹 −𝐶𝐶𝐶𝐶𝐶𝐶 𝐶𝐶𝐶𝐶𝐶𝐶 where Cij= Capacity of the link and Fi j = Link flow, sketch
the cost function on the graph shown below and hence comment whether this is a suitable cost function to use in
optimal routing problems or not?
A cost function is suitable if its cost rises as the flow on that link
increases and vice versa. From graph, we see that the cost decreases as
the flow increases, hence this is NOT a suitable cost function to use in
optimal routing.
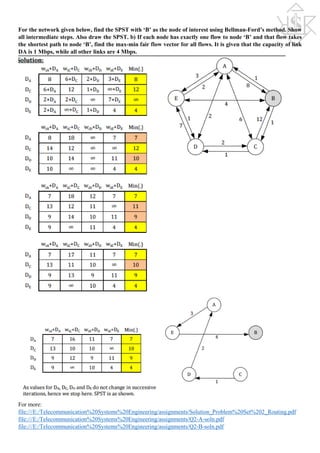
For the flows shown in Figure 2, find the max-min fair flow vector, given that all links have a capacity of 8 Mbps.
Also determine the bottleneck link(s) for each session.
So, r1 = r2 = r3 = r4 = 2 are maximally allocated, leaving sessions 5 and 6
as minimally allocated sessions with rates r5 = r6 = 2
Hence link (3,5) is the bottleneck link for sessions 5 and 6 So, r5 = r6 =
3 are now maximally allocated. As all sessions have been maximally
allocated, hence we stop our iterations. The final flow vector r, hence
becomes: [r1, r2, r3, r4, r5, r6] = [2, 2, 2, 2, 3, 3]
Find the max-min fair flow vector for the traffic flows shown in Figure 3 below. Also identify the bottleneck link
for each flow.

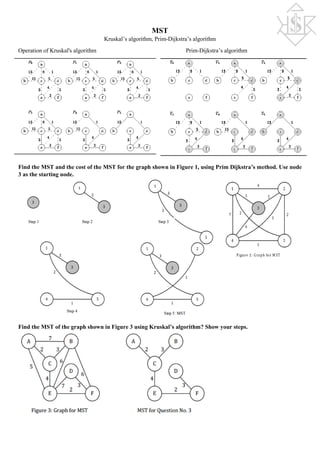
10. Given that each node has exactly one flow to node B, we can redraw the above figure to include flows that take
the shortest path from each node to our node of interest i.e. node B.
Flows rCA and rDA cause link DB to overflow, hence they are stopped
at 1.5 Mbps. Hence, flow vector after 1st iteration is: [rCA, rDA, rBA,
rEA] = [1.5, 1.5, 1.5, 1.5] Iteration 2:
Flows 𝑟𝑟𝐵𝐵𝐵𝐵 𝑎𝑎𝑎𝑎𝑎𝑎 𝑟𝑟𝐸𝐸𝐸𝐸 cause link EA to overflow, hence they are stopped after an increment of 1 Mbps at 2.5 Mbps.
Hence, max-min fair flow vector is: [𝑟𝑟𝐶𝐶𝐶𝐶, 𝑟𝑟𝐷𝐷𝐷𝐷, 𝑟𝑟𝐵𝐵𝐵𝐵, 𝑟𝑟𝐸𝐸𝐸𝐸] = [1.5, 1.5, 2.5, 2.5]
Given that each node has exactly one flow to node B, we can redraw the above figure to include flows that take
the shortest path from each node to our node of interest i.e. node B.
Flows rCB and rDB cause overflow at link EB, which is hence a
bottleneck link for these flows. Hence, max-min fair flow vector after
Iteration 1 is: [𝑟𝑟𝐶𝐶𝐶𝐶, 𝑟𝑟𝐷𝐷𝐷𝐷, 𝑟𝑟𝐴𝐴𝐴𝐴, 𝑟𝑟𝐸𝐸𝐸𝐸] = [0.5, 0.5, 0.5, 0.5]
Flows rAB and rEB cause link EB to overflow, hence they are stopped after an increment of 1 Mbps at 1.5 Mbps.
Hence, max-min fair flow vector is:[𝑟𝑟𝐶𝐶𝐶𝐶, 𝑟𝑟𝐷𝐷𝐷𝐷, 𝑟𝑟𝐵𝐵𝐵𝐵, 𝑟𝑟𝐸𝐸𝐸𝐸] = [0.5, 0.5, 1.5, 1.5]
Determine whether the flow distribution; for the Figure 2 above; is max-min fair or not. The capacity of all links
is 5 Mbps, except link (2,5) whose capacity is 25 Mbps.
For testing bottleneck links, we increase a flow by a small amount and observe which links overflow. If the link that
overflows, has that flow as the largest flow, then that link is the bottleneck link for that flow.
As flow has no associated bottleneck link, hence the distribution is NOT Max-Min fair.

11. Find the max-min fair flow vector for all flows. The capacity of all links is 5 Mbps, except link (2,5) whose capacity
is 25 Mbps.
Given the capacity of all links is C = 1 Mbps, assign the rates to the sessions using the max min fairness flow
control mechanism for the network shown in Figure 2.
SDH SONET
If a voice signal is sampled at a rate of 16000 samples per second, instead of the 8000 samples per second as in
PCM, what would have been the basic rate of E1 (employing 32 time slots) and T1 (employing 24 time slots and 1
framing bit)?
Solution:
Time for 1 sample = 1/16000 = 62.5 ms
Date rate = frame size / sample time
Date rate for E1 = (32 x 8) / 62.5 x 10–6 = 4.096 Mbit/s
Data rate for T1 = (24 x 8 + 1) / 62. 5 x 10–6 = 193 / 62.5 x 10–6 = 3.088 Mbit/s
Data rate = frame size x sampling rate
Date rate for E1 = (32 x 8) x 16000 = 4.096 Mbit/s
Data rate for T1 = (24 x 8 + 1) x 16000 = 193 / 62.5 x 10–6 = 3.088 Mbit/s
Transmission rate of T1 = 24 x 8 + 1 = 193 bits per 125
ms = 1.544 Mbit/s
Transmission rate of E1 = 32 x 8 = 256 bits per
125 ms = 2.048 Mbit/s

12. • Information transmitted by SDH/SONET is organized into frames
• Each frame consists of payload and overhead
• SDH/SONET are also defined to carry ATM cells, and PPP and HDLC frames
• Frames are constructed in electrical domain and transmitted in optical domain
• Electrical side of SDH is known as Synchronous Transport Module (STM), while that of SONET is known as
Synchronous Transport Signal (STS)
• Optical side of both SDH and SONET is known as the Optical Carrier (OC)
Find the data rate of the optical communication system using a synchronous transport signal level 18 (STS-18) ?
For STS-1, the total number of transmission bits are: 90 x 9 x 8 = 6480 bits
For STS-18, the total number of transmission bits are: 90 x 9 x 8 x 18 = 116640 bits
Therefore, the data rate of STS-18 is: 116640 bits x 8000 samples/second = 933.12 Mbps
If the payload and overhead rates of STS-12 are 601.344 Mbit/s and 20.736 Mbit/s respectively, what will be the
data rate of STM-8?
Payload rate of STM-8 = STS-24 = 2xSTS-12 = 1202.688 Mbps
Overhead rate of STM-8 = 2 x 20.736 = 41.472 Mbps
Data rate of STM-8 = 1202.688 + 41.472 = 1244.16 Mbps
If the rate of STM-12 is 1866 Mbps, what will be the rate of STS-18?
Rate of: STM-12 = STS-36 Hence rate of STS-18 = STS-36/2 = STM-12/2 = 1866/2 = 933 Mbps
If the rate of STM-4 is 622 Mbps, what will be the rate of STS-24?
Rate of: STM-4 = STS-12 Hence rate of STS-24 = 2 x STS-12 = 2 x STM-4 = 622 x 2 = 1244 Mbps
Pakistan Centre for Optical Networks (PakCON) decided that the European base rate E1 and American base rate
T1 was not quite appropriate for telephone networks in Pakistan due to the dense population of users in the urban
areas and hence decided to have their own hierarchy with a base rate of P1. The frame structure is as shown in
Figure below.
Given that the voice signals are digitized at 10000 samples per second, and that the amplitude of the signal is
represented by a 10-bit number, answer the following questions: i. What is the transmission rate of P1? ii. What
is the transmission rate of the payload and overhead?
Find the data rate of the optical communication system using a synchronous transport signal level 18 (STS-18) ?
For STS-1, the total number of transmission bits are: 90 x 9 x 8 = 6480 bits
For STS-18, the total number of transmission bits are: 90 x 9 x 8 x 18 = 116640 bits
Therefore, the data rate of STS-18 is: 116640 bits x 8000 samples/second = 933.12 Mbps

13. Fiber Span Analysis
A 96-km long SSMF with a core radius of 8.1µm is used to transmit an optical signal from CIIT Islamabad to
CIIT Abbottabad. Termination of the fiber is done through a patch panel at both ends and LC connectors are
used for connection from/to the transmitter/receiver. If the span loss is 29.7 dB, the maximum and minimum
receiver sensitivity is –3 dBm and –30 dBm respectively, and given that the system is viable; i) What will be the
minimum and maximum power ratings of the transmitter (in dBm and milliwatts)? ii) What are the various losses
and their values that will contribute to the span loss of 29.7 dB? iii) The ITS department of CIIT wants to connect
CIIT Wah to this network by inserting a passive splitter with equal distribution of power at both outputs of the
1:2 splitter after 48 km of this fiber. Discuss briefly, the implications of this action on the viability of the existing
system.
iii) When a splitter is inserted halfway, it will split the power of the received signal at that point into two equal parts,
thereby reducing the power of that signal by half. Thus the span loss for the CIIT Islamabad to CIIT Abbottabad will
increase significantly and the system will no longer remain viable.
CIIT Islamabad is connected to Center of Technology, Abbottabad, through a 100km long single-mode fiber as
shown in the figure below. The fiber span contains 10 fusion splices. Termination at both ends is done through
patch panels using LC connectors. If the intended transmission rate is 10Gbit/s, the minimum and maximum
transmitter launch powers are -10 dBm and 0 dbm at 1550nm respectively, and the system proposed is viable,
what should be the minimum and maximum receiver sensitivity in dBm and mW.
Given:
PTMIN = –10 dBm
PTMAX = 0 dBm, at 1550 nm
For a viable system, Span loss (PS) should be within the Power
Budget (PB), i.e., the Power Margin (PM) should be greater than
or equal to zero.
(PM = PB – PS) ≥ 0, hence:
PB – PS ≥ 0 => –10 – x – 30.7 ≥ 0 => x ≤ –40.7
or PRMIN ≤ –40.7 dBm,
or PRMIN ≤ 8.511x10-5
mW
Also, to prevent receiver saturation, the received input power
must not exceed maximum receiver sensitivity, in a viable
system,
i.e., PRMAX ≥ (PIN = PTMAX – PS)
Hence,
PRMAX ≥ 0 – 30.7 => PRMAX ≥ –30.7 dBm
or PRMAX ≥ 8.511 x 10-4
mW
(Note: As maximum power on the SMF is below +10dBm, hence non-linear losses could be ignored, but as data rate is
very high ~10Gbps, they should be considered)
You have to lay a fiber from your come to CIIT Islamabad. Using any online map find the distance from you
home to CIIT and also attach its print with this assignment. You have maximum Optical Fiber Cable length of 1

14. km, above that you have to joint another OFC. You are using single mode OFC. All splices are fusion. Termination
at both ends is done through patch panels using LC connectors. If the intended transmission rate is 10Gbit/s, the
minimum and maximum transmitter launch powers are -10 dBm and 0 dbm at 1550nm respectively, and the
system proposed is viable, what should be the minimum and maximum receiver sensitivity in dBm and mW.
Cryptography
A user's data is encrypted using a transposition cipher with key ERA. If the output of the
transposition cipher is: OSOTOTTTHTOHOOO The user's original data?
Decoding Transposition Cipher to get the User data at A: We note that cipher text has 15
symbols while the key has 3, so forming groups of 5 symbols and placing them column-
wise under the alphabets of the key in numeric order, we get: Now reading row-wise, we
get the user data i.e. TOOTHSTOOHOTTOO
Queuing Theory
M/M/1 queue State Space Diagram:
Utilization: 𝜌𝜌=𝜆𝜆/𝜇𝜇
Average total number of customers in the system:
Total time spend in the system:
1
𝜇𝜇−𝜆𝜆
Average time spent waiting in the queue:
1
𝜇𝜇−𝜆𝜆
–
1
𝜇𝜇
Finally, the average number of customers in the buffer can be obtained
M/M/C State space diagram:
Utilization: 𝜌𝜌 =
𝜆𝜆
𝑐𝑐𝑐𝑐
Average number of customers in the system:
𝜌𝜌
1−𝜌𝜌
𝐷𝐷 + 𝑐𝑐𝑐𝑐 𝐷𝐷 =
1
1+(1−𝜌𝜌)
𝑐𝑐!
(𝑐𝑐𝑐𝑐)𝑐𝑐 ∑
(𝑐𝑐𝑐𝑐) 𝑘𝑘
𝑘𝑘!
𝑐𝑐−1
𝑘𝑘=0
Average time spent waiting in the queue:
𝐷𝐷
𝑐𝑐𝑐𝑐−𝜆𝜆
+
1
𝜇𝜇
Consider an M/M/1 system and calculate the average total time spent in the queue by the customer, if the service
rate is µ = 50 customers/minute. The average number of customers in the system are 4.
Consider an M/M/1 queueing system. Customer interarrival times have an average of minutes, and service times
have an average of 4 minutes. What will be the average number of customers waiting in line?
Customers arrive at a fast food restaurant at a rate of 100 per hour and take 30 seconds to be served.
How much time do they spend in the restaurant? Service rate = µ = 60/0.5=120 customers per hour – T = 1/µ−λ =
1/(120-100) = 1/20 hrs = 3 minutes
How much time waiting in line? – W = T - 1/µ = 2.5 minutes
How many customers in the restaurant? – N = λT = 5
What is the server utilization? – ρ = λ/µ = 5/6
Fundamentals of Cellular Network Planning