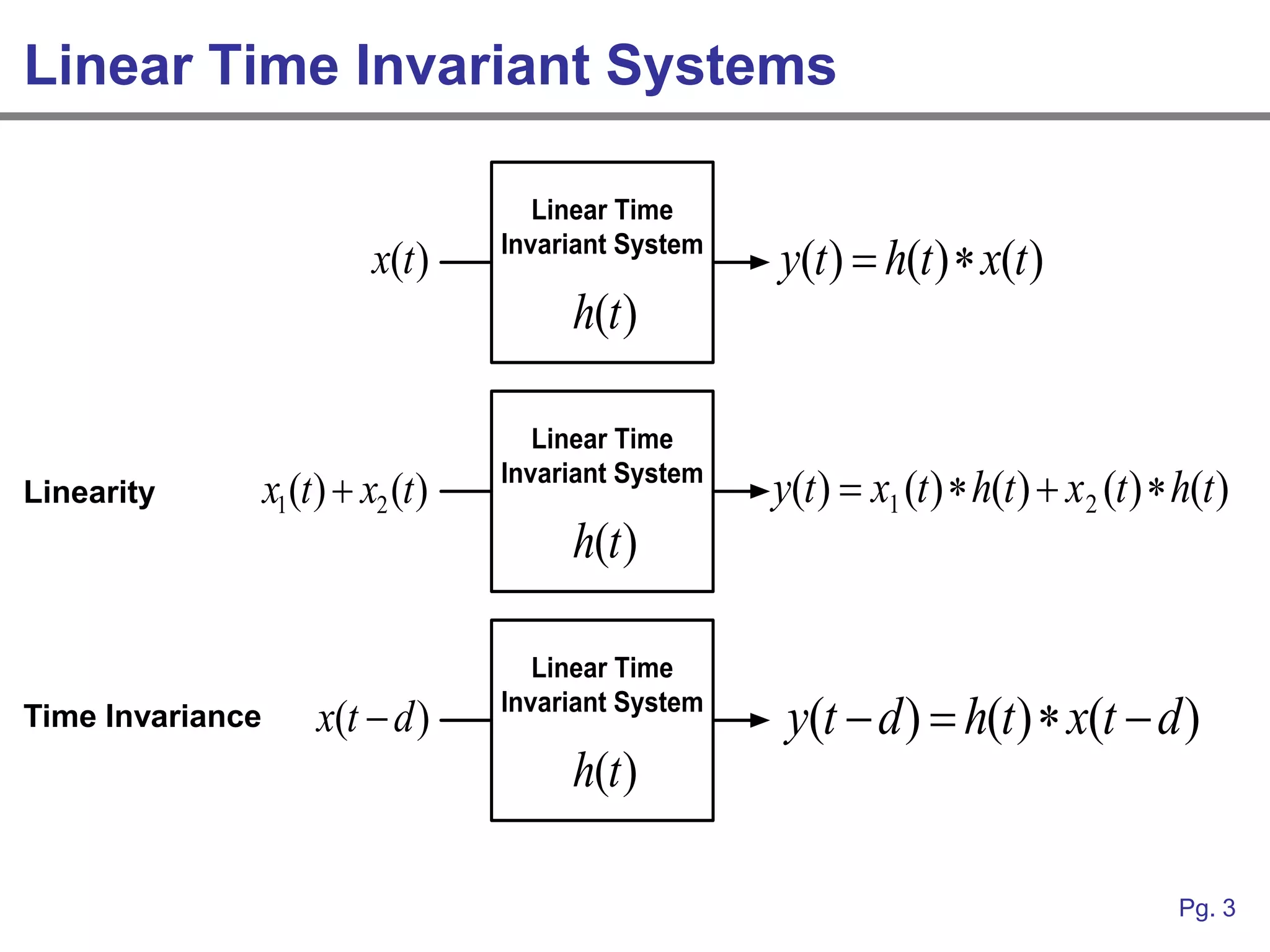
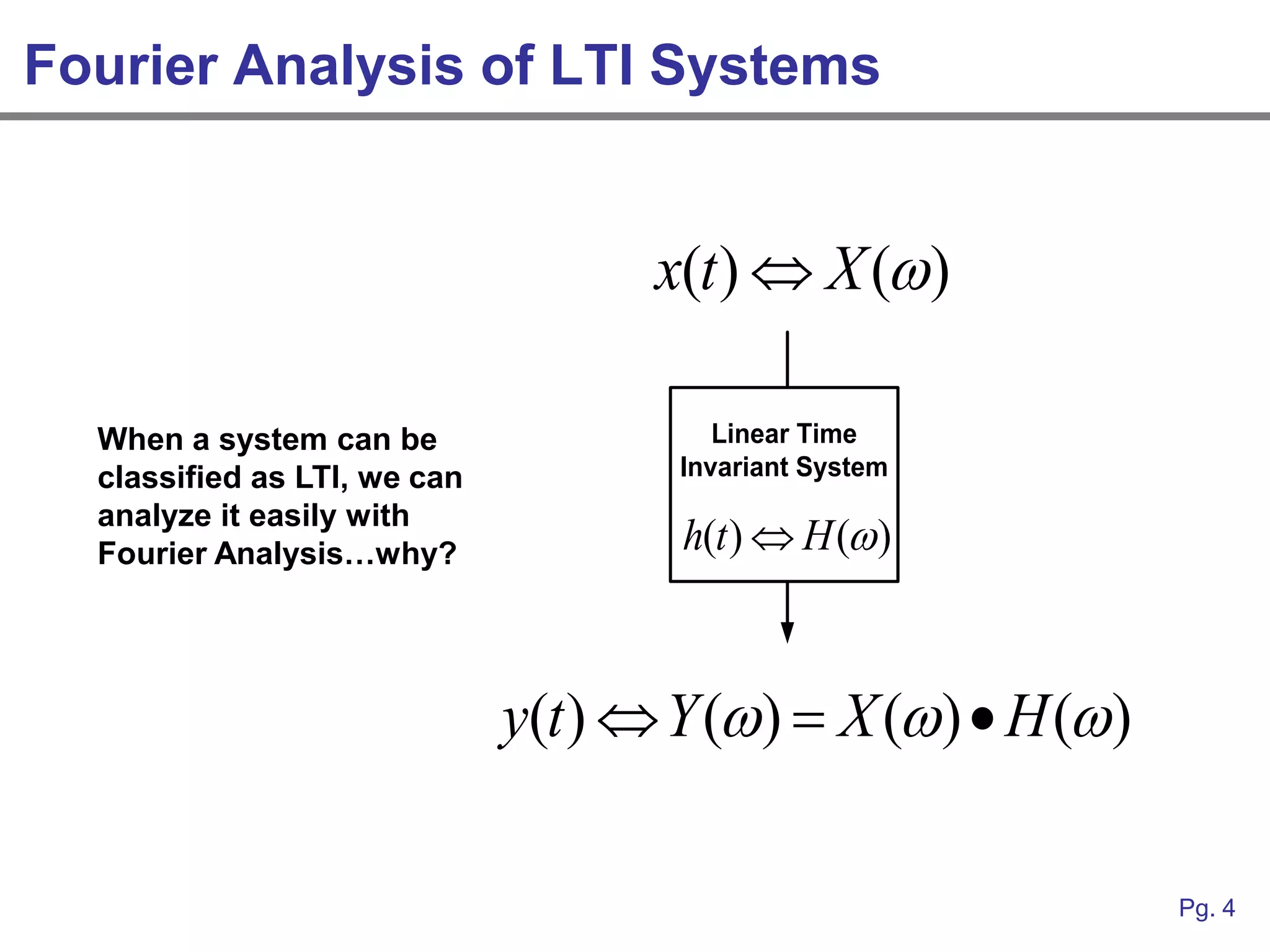
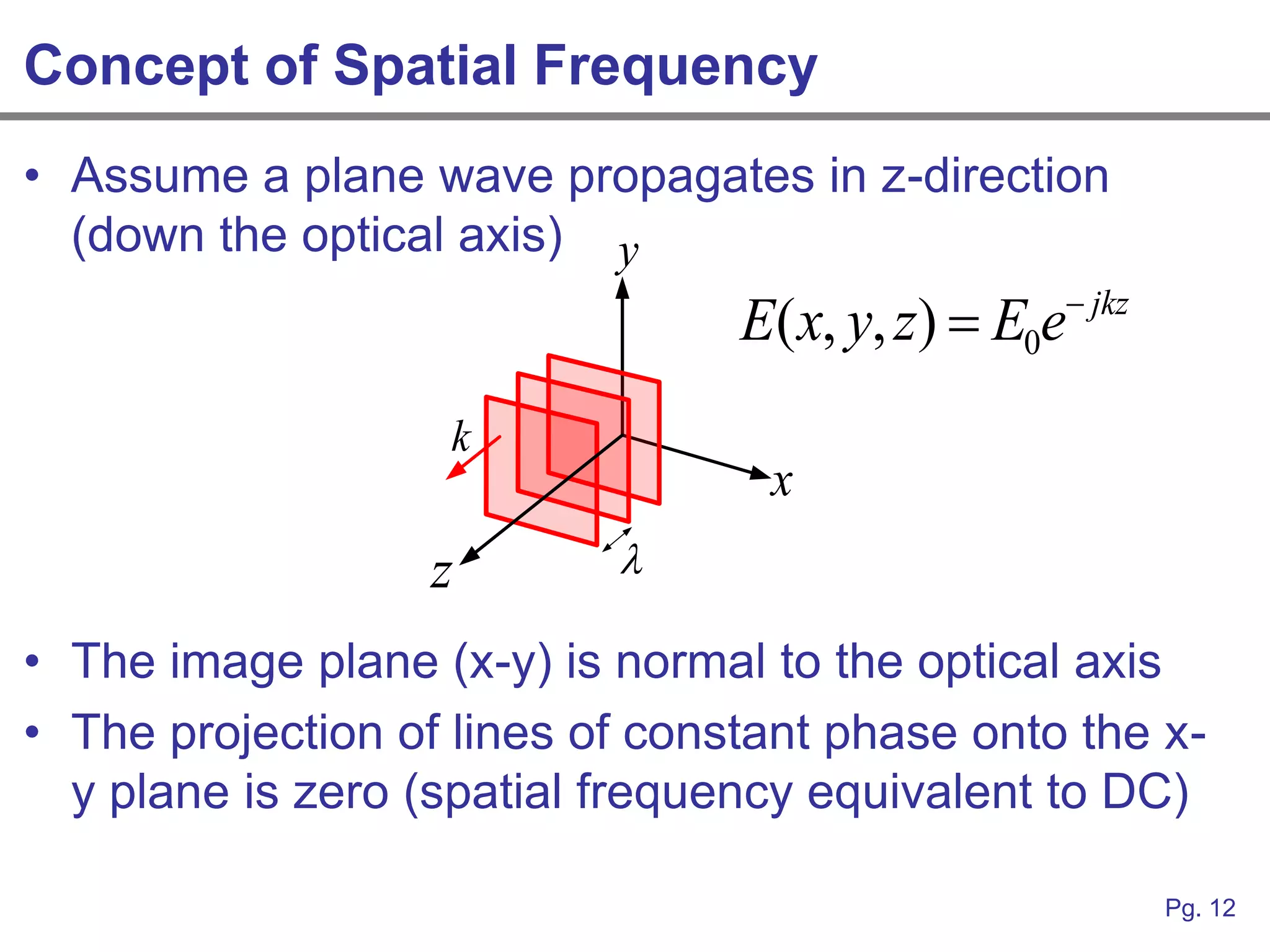
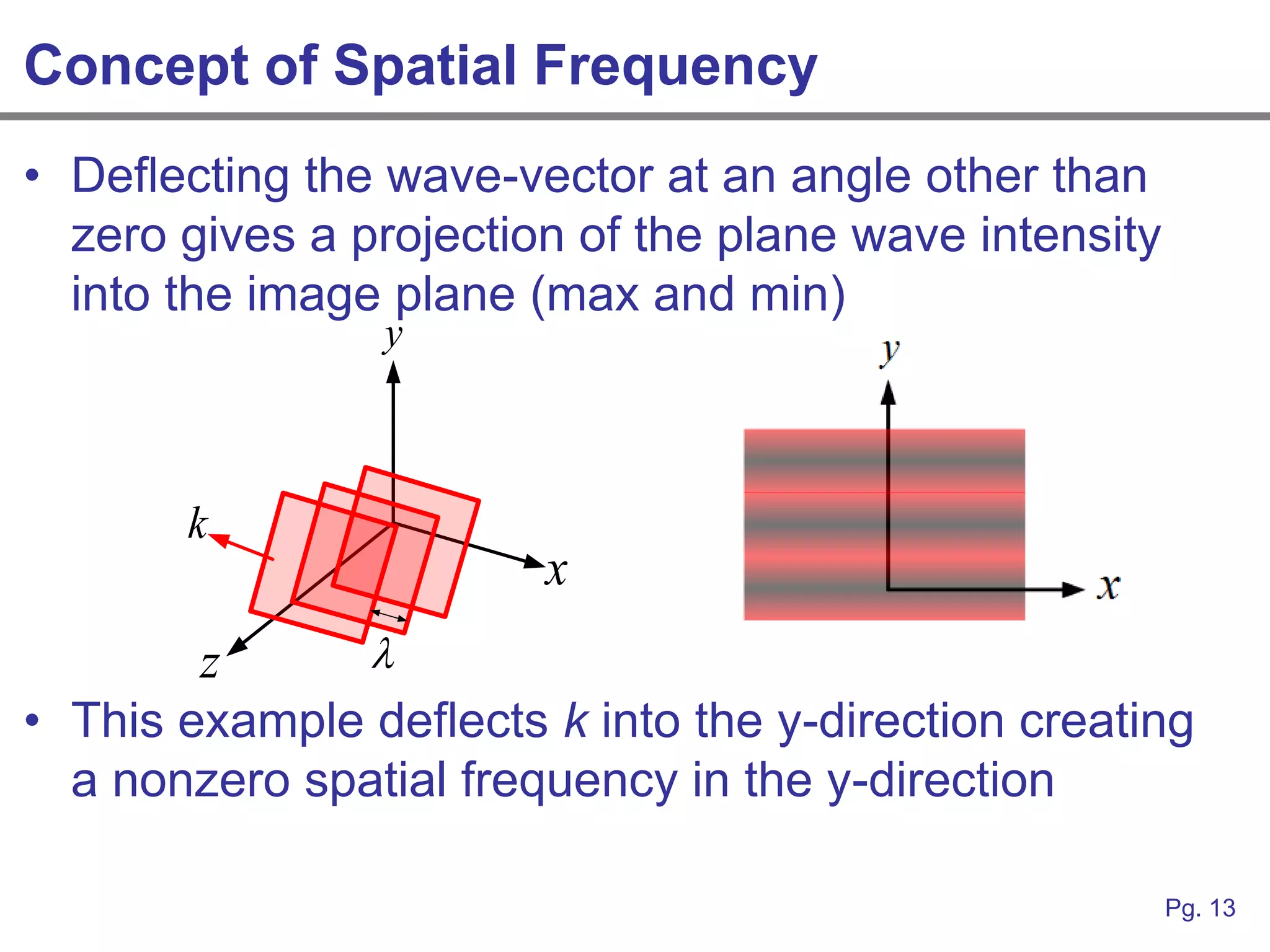
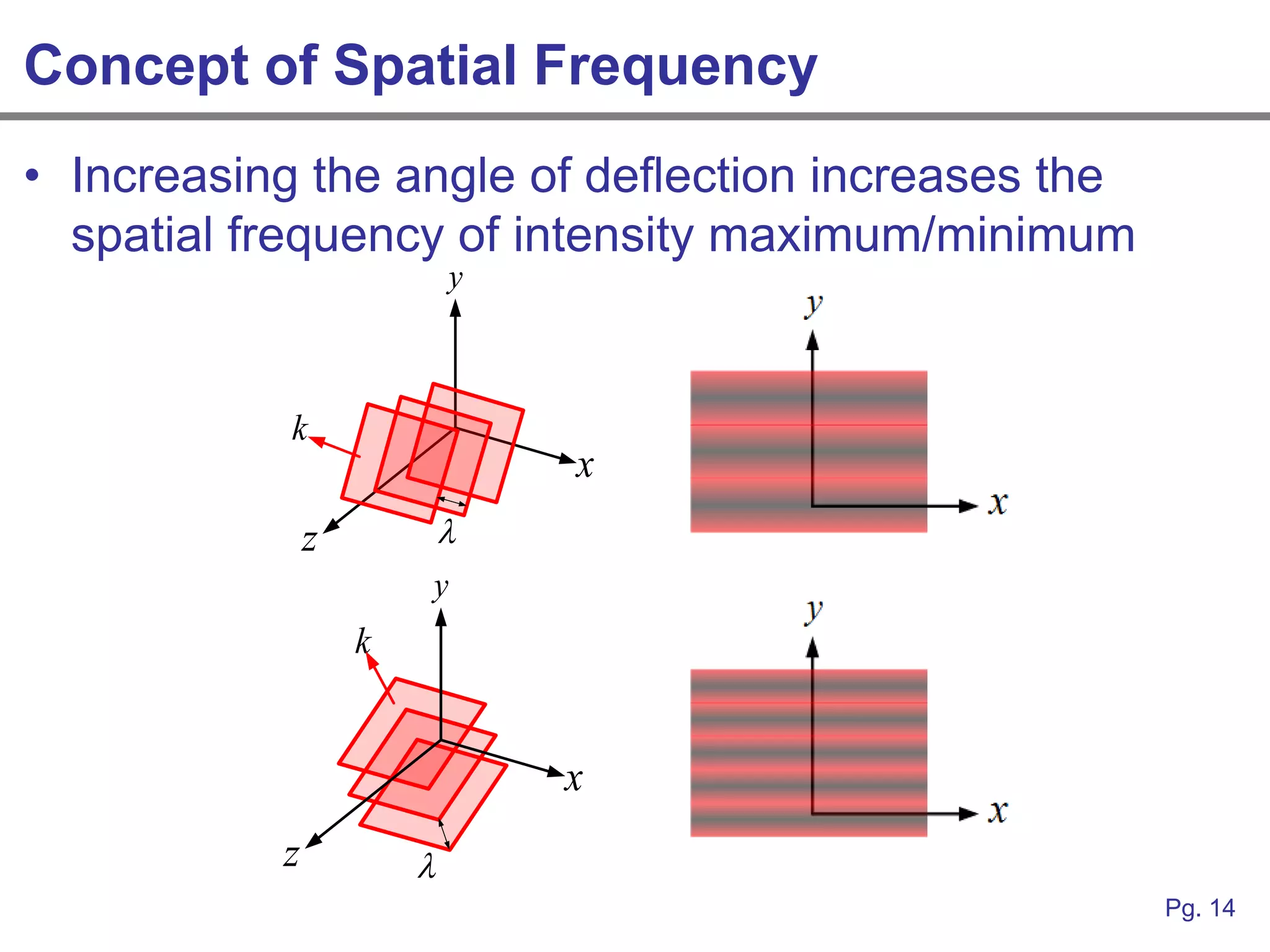
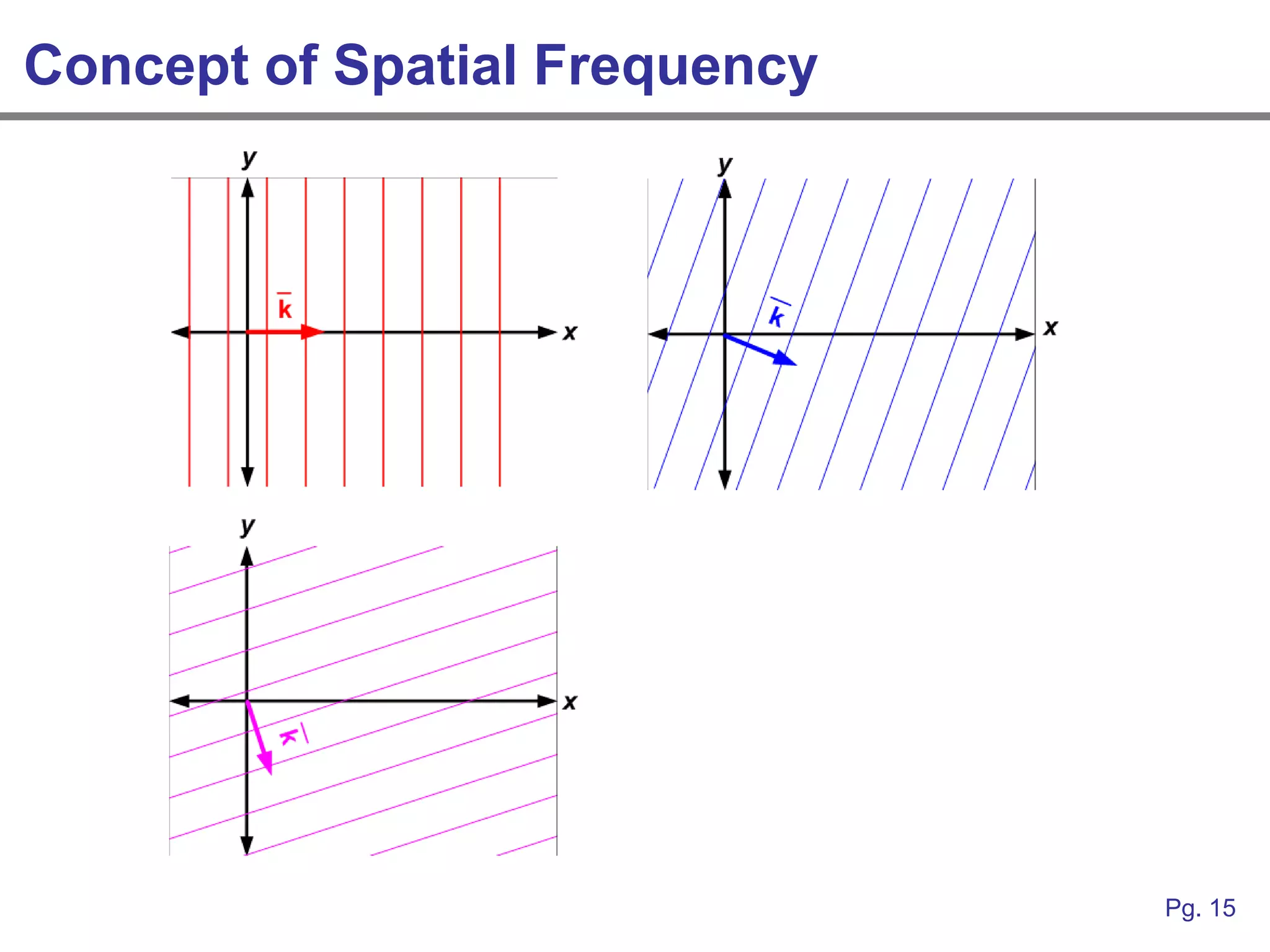
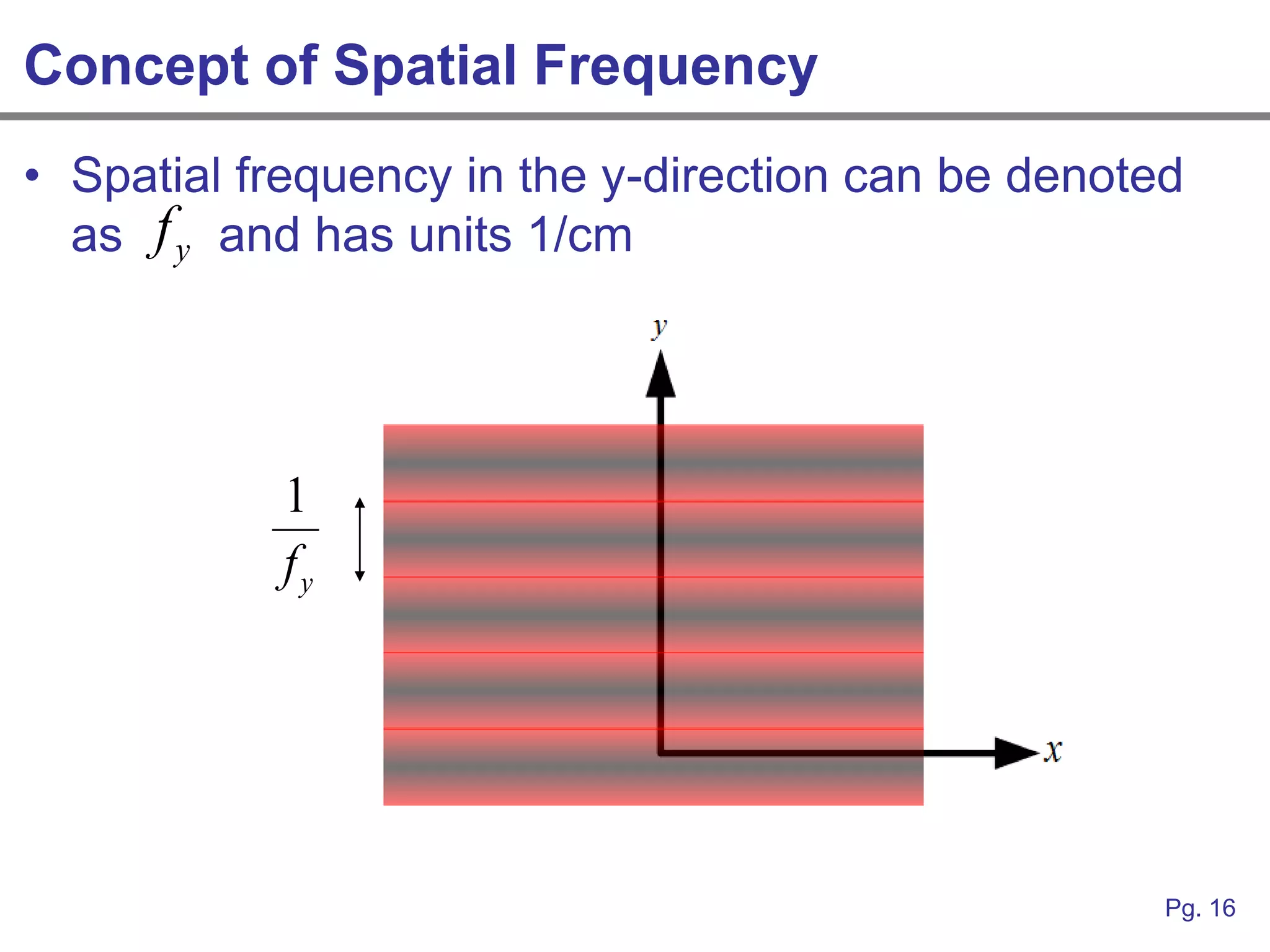
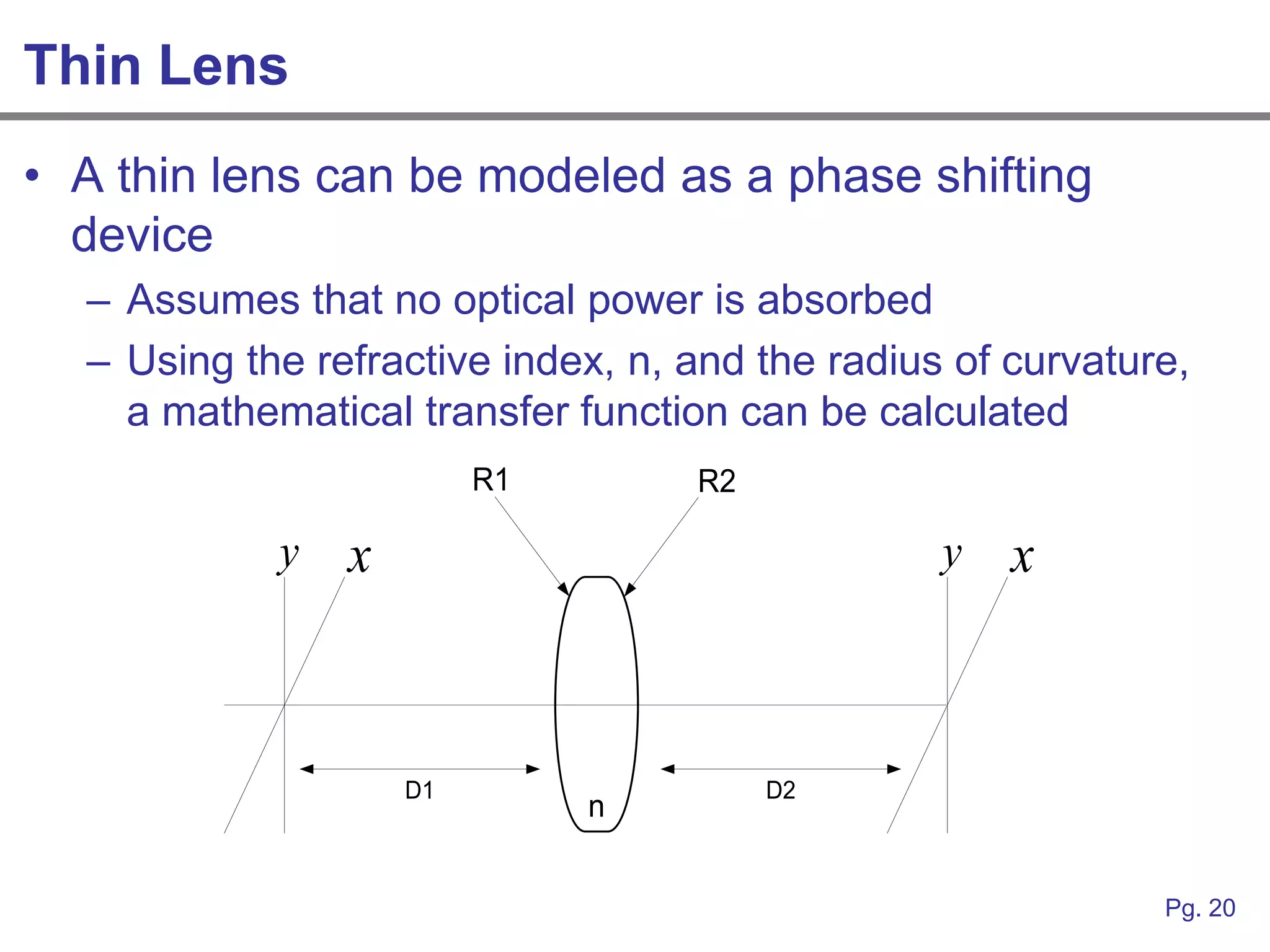
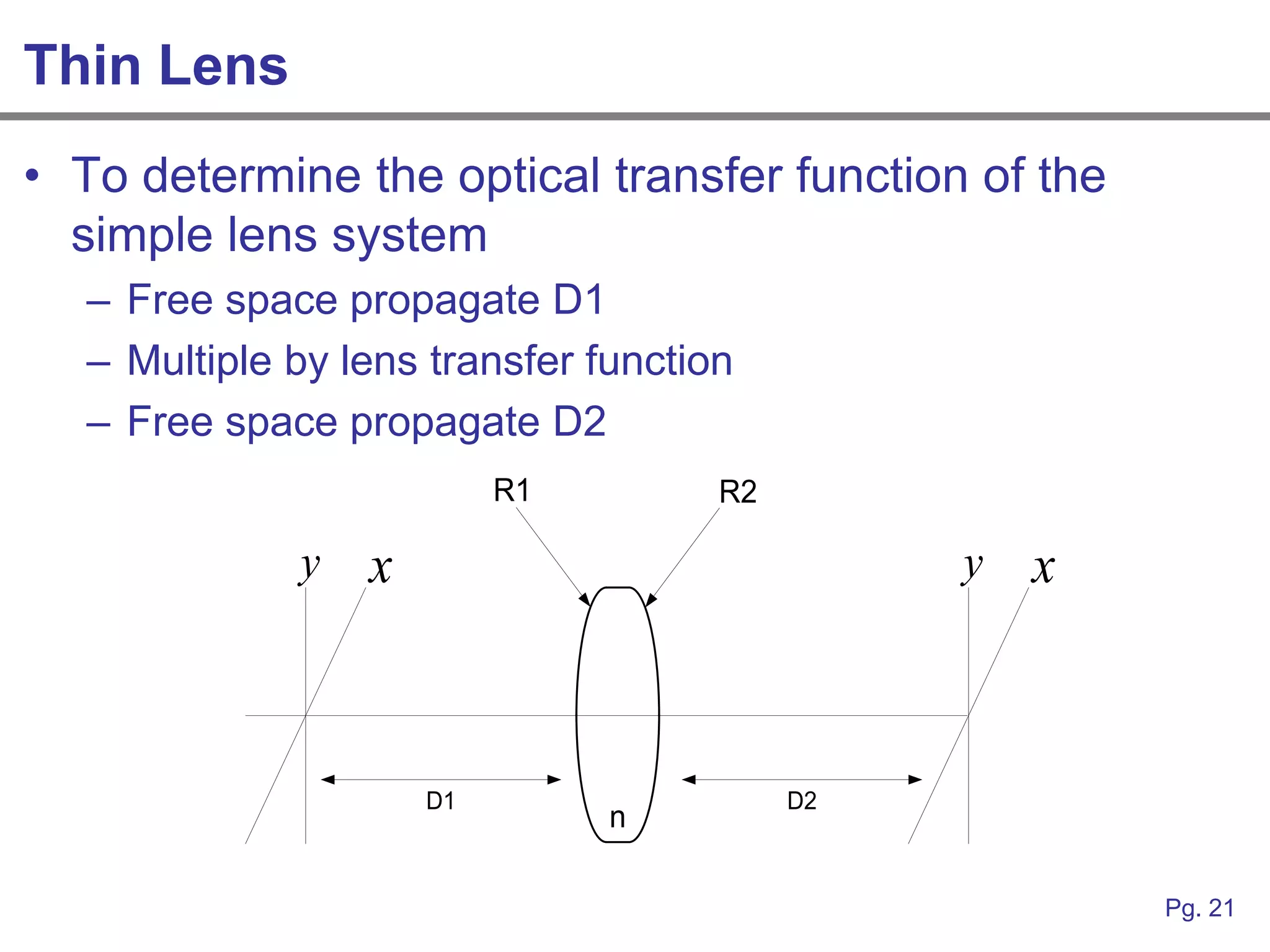
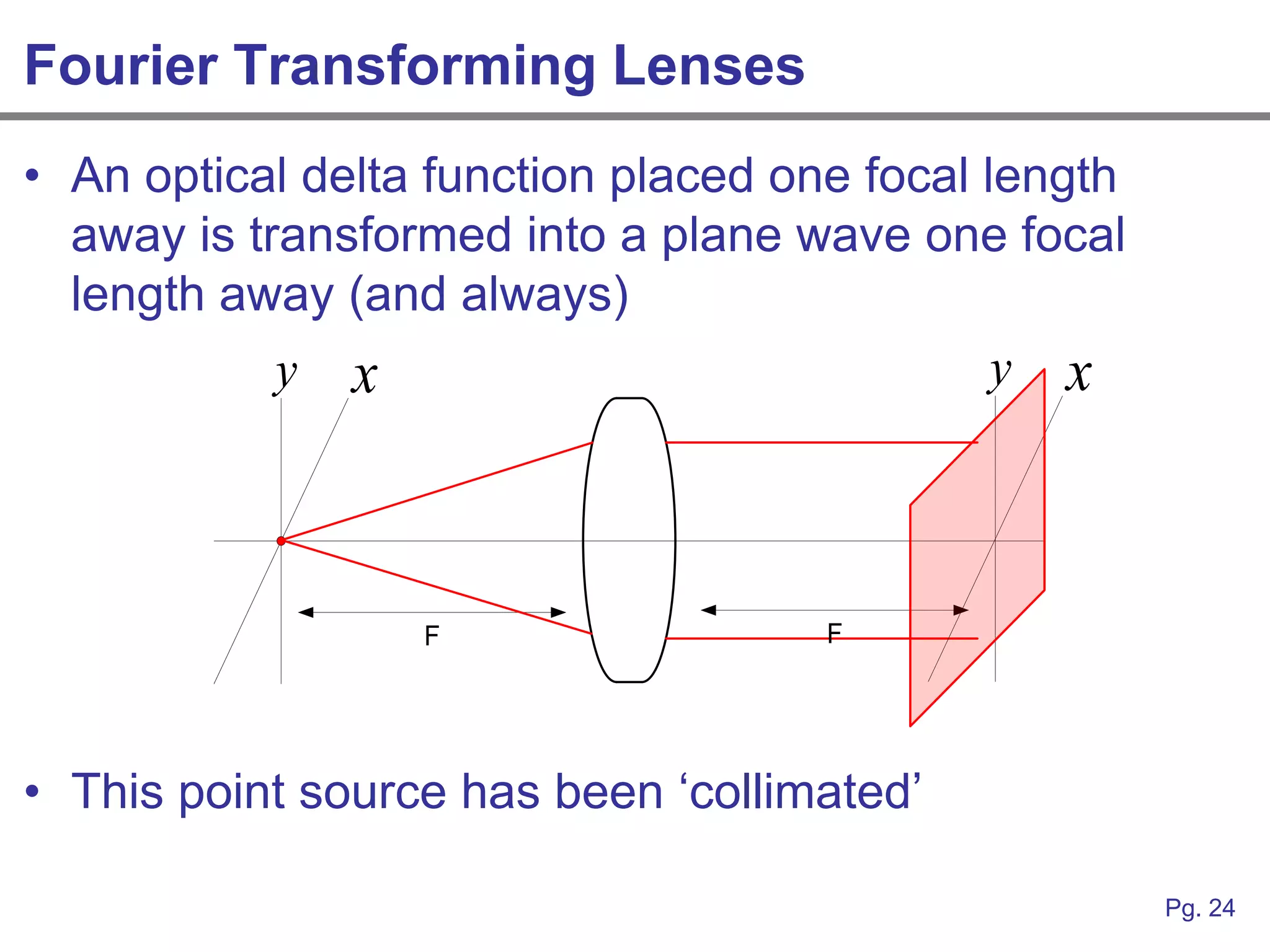
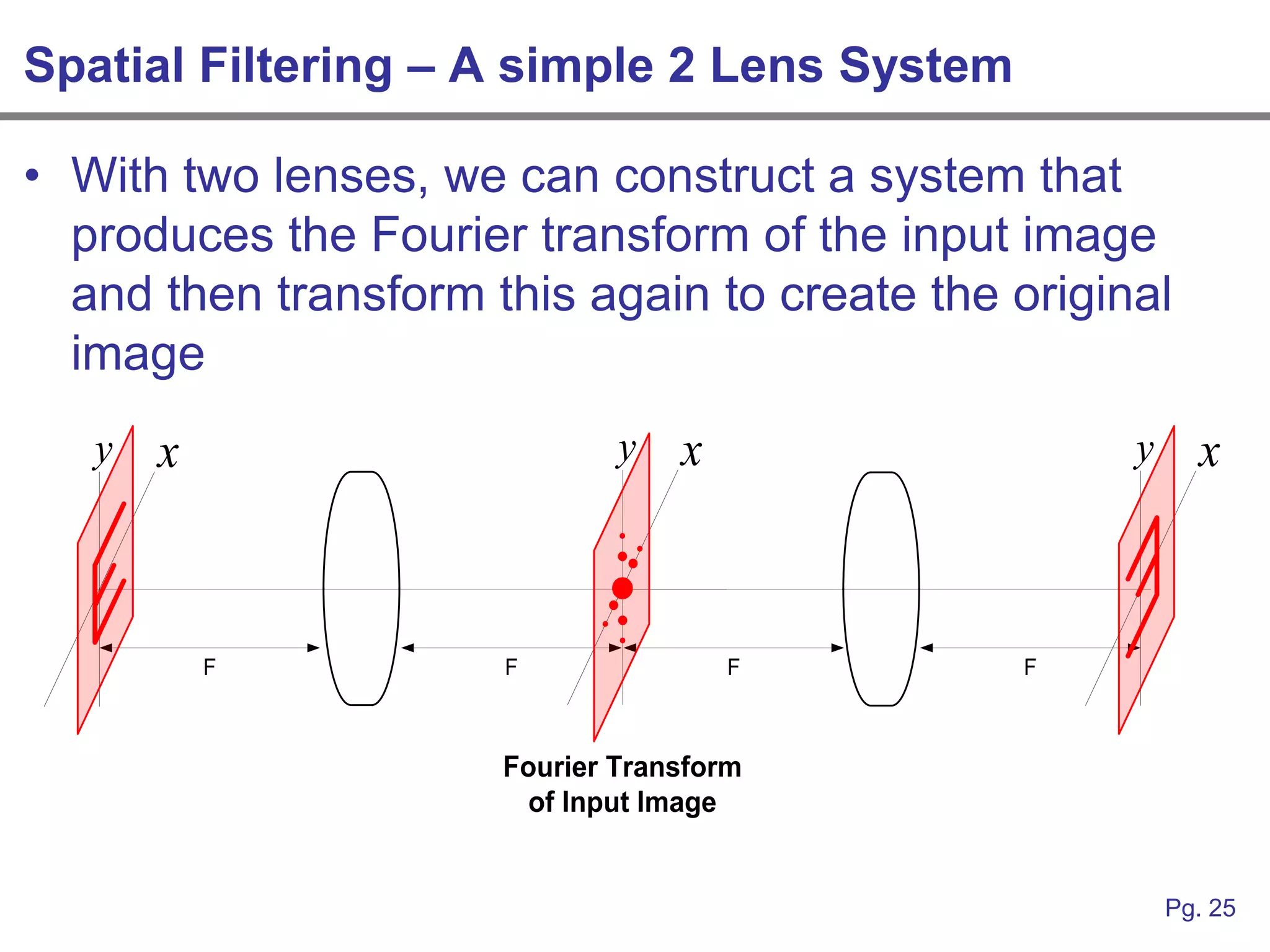
This document provides an overview of how linear systems analysis and Fourier transforms can be applied to analyze 2-dimensional optical images and optical systems. It explains that plane waves serve as the eigenfunctions for linear shift invariant optical systems, just as complex exponentials serve as the eigenfunctions for linear time invariant electrical systems. The Fourier transform can be used to decompose an optical image into its plane wave spectrum, and optical systems can be analyzed by multiplying the image spectrum by the system's optical transfer function and taking the inverse Fourier transform. As an example, it describes how a thin lens can be modeled as a phase shifting device and its optical transfer function calculated.

1. Application of Linear Systems
Analysis to 2-D Optical Images
(Fourier Optics)
An Intuitive Approach
Andrew Josephson
ajosephson@comcast.net
Pg. 1

2. Fourier Transforms of Electrical Signals
• As electrical engineers, we conceptualize the
Fourier transformation and Fourier synthesis of
voltages and currents frequently in circuit analysis
• Why do we use the Fourier Transform?
• There are other transforms
– Hilbert
– Hankel
– Abel
– Radon
• What makes the Fourier Transform special?
Pg. 2

3. Linear Time Invariant Systems
Linear Time
x(t ) Invariant System
y(t )  h(t )  x(t )
h(t )
Linear Time
Linearity x1(t )  x2 (t ) Invariant System
y(t )  x1 (t )  h(t )  x2 (t )  h(t )
h(t )
Linear Time
Time Invariance x(t  d ) Invariant System
y(t  d )  h(t )  x(t  d )
h(t )
Pg. 3

4. Fourier Analysis of LTI Systems
x(t )  X ( )
When a system can be Linear Time
classified as LTI, we can Invariant System
h(t )  H ( )
analyze it easily with
Fourier Analysis…why?
y(t )  Y ( )  X ( )  H ( )
Pg. 4

5. Eigen Function of LTI Systems
• The Eigen function of an LTI system is a
mathematical function of time, that when applied as
a system input, results in a system output of
identical mathematical from
– The output equals the input scaled by a constant „A‟
– Delayed in time by „d‟
Linear Time
 (t ) Invariant System
y(t )  h(t )  (t )  A  (t  d )
h(t )
Pg. 5

6. Eigen Function of LTI Systems
• Complex exponentials are the Eigen functions of LTI
systems
(t )  e  jt
• Complex exponentials are also the Kernel of the
Fourier Integral
1 
X ( )  
 jt
x(t )e dt
2 
Pg. 6

7. Fourier Analysis of LTI Systems Revisited
• Conceptually, when we analyze
an LTI system, we represent the
input signal x(t) as a summation
x(t )  c0  c1e j1t  c2e j2t  ...
of linearly scaled Eigen functions
(complex exponentials)
– Fourier Decomposition
Linear Time
– The signal‟s “spectrum” Invariant System
• We can then run each complex
exponential through the system h(t )
easily because they give rise to a
linearly scaled output that is
delayed in time
y(t )  K0c0  K1c1e j1 (t d )  K2c2e j2 (t d )  ...
• The output y(t) is the summation
of these scaled and delayed
complex exponentials
Pg. 7

8. Answer to the Million Dollar Question
• We use the Fourier Transform to analyze LTI
systems because the Eigen function of an LTI
system IS the Kernel of the Fourier Integral
• When we do not have an LTI system, we usually
assume it is closely approximated by one, or force it
to operate in a well-behaved region
– Linearization
• The complex exponentials we deal with in circuits
are single variable functions with independent
variable „t‟
• Where else in electrical engineering do we use
complex exponentials?
Pg. 8

9. Plane Waves
• Complex exponentials are also used to describe
plane waves
– The plane defines a surface of constant phase
• These are multivariate functions with independent
variables R = (x,y,z)
z
k  jkR
R E(R)  E0e
x
y
Pg. 9

10. Plane Waves as Eigen Functions
• Plane waves are Eigen functions of certain system
types as well
– Since the independent variable is no longer time, we
aren‟t interested in Linear Time Invariant Systems
• We are now interested in the more general Linear
Shift Invariant System
– Shift refers to spatial movement since the independent
variables now describe position instead of time
Pg. 10

11. Fourier Optics
• Fourier Optics is the application of linear shift
invariant system theory to optical systems
• The plane wave in an optical system is represented
by the multivariate complex exponential just like the
sine wave in an LTI system is represented by the
 jt
single variable e
• Just like an electrical signal can be represented as
summation of sine waves, an optical image can be
represented as a summation of plane waves
– Angular Plane Wave Spectrum
Pg. 11

12. Concept of Spatial Frequency
• Assume a plane wave propagates in z-direction
(down the optical axis) y
 jkz
E( x, y, z)  E0e
k
x
z 
• The image plane (x-y) is normal to the optical axis
• The projection of lines of constant phase onto the x-
y plane is zero (spatial frequency equivalent to DC)
Pg. 12

13. Concept of Spatial Frequency
• Deflecting the wave-vector at an angle other than
zero gives a projection of the plane wave intensity
into the image plane (max and min)
y
k
x
z 
• This example deflects k into the y-direction creating
a nonzero spatial frequency in the y-direction
Pg. 13

14. Concept of Spatial Frequency
• Increasing the angle of deflection increases the
spatial frequency of intensity maximum/minimum
y
k
x
z 
y
k
x
z 
Pg. 14

15. Concept of Spatial Frequency
Pg. 15

16. Concept of Spatial Frequency
• Spatial frequency in the y-direction can be denoted
as f y and has units 1/cm
1
fy
Pg. 16

17. Angular Plane Wave Spectrum
• An arbitrary 2-D field distribution (image) can be decomposed
into a spectrum of plane waves
– Assuming monochromatic light
• Just like the Fourier Transform of an electrical signal
represents the magnitude and phase of each sinusoid in the
signal spectrum, the 2-D Fourier Transform of an image
represents the magnitude and phase of each plane wave in
the image spectrum
• High spatial frequency -> plane wave at large angles
• Low spatial frequency -> plane wave at small angles
Pg. 17

18. 2-D Fourier Transform
• Consider an arbitrary 2-D black and white image in
the XY-Plane
• The image can be described mathematically by
some function U(x,y,z=0)
– „U‟ is optical intensity versus position
2
– Optical intensity is just proportional to E
• The angular plane wave spectrum of the image is
related to the 2-D Fourier Transform

A( f X , fY )   U ( x, y, z  0) exp j 2  f X x  fY y df X dfY

Pg. 18

19. LSI Optical Systems
• In Linear Shift Invariant optical systems, we can use
Fourier analysis to decompose an image into its
spectrum, multiply the spectrum by the optical
transfer function(s), and inverse transform to get the
resulting output
– Note: Free space propagation of optical images can be
modeled as an LSI system
– This technique correctly models diffraction
– This technique produces identical results to the full
Rayleigh-Sommerfeld solutions
Pg. 19

20. Thin Lens
• A thin lens can be modeled as a phase shifting
device
– Assumes that no optical power is absorbed
– Using the refractive index, n, and the radius of curvature,
a mathematical transfer function can be calculated
R1 R2
y x y x
D1 D2
n
Pg. 20

21. Thin Lens
• To determine the optical transfer function of the
simple lens system
– Free space propagate D1
– Multiple by lens transfer function
– Free space propagate D2
R1 R2
y x y x
D1 D2
n
Pg. 21

22. Fourier Transforming Lenses
• A special value of D1 exists where many terms in
the optical transfer function simplify
1
D1 
1 1
n 1  
R R 
 1 2
– This special value is called the focal length
– When the input image is placed one focal length away, the
optical transfer function at one focal length after the lens
becomes a 2-D Fourier Transformation of the input image
– Most of us already kinda knew that…
Pg. 22

23. Fourier Transforming Lenses
• A delta function and sine wave (complex
exponential) form a Fourier Transform pair
• What is the image equivalent of a delta function?
– A point of light
• We know that a plane wave is a complex
exponential
– A point of light and a plane wave form a Fourier Transform
Pair
• This is exactly what happens when we place a point
of light one focal length away from a lens
Pg. 23

24. Fourier Transforming Lenses
• An optical delta function placed one focal length
away is transformed into a plane wave one focal
length away (and always)
y x y x
F F
• This point source has been „collimated‟
Pg. 24

25. Spatial Filtering – A simple 2 Lens System
• With two lenses, we can construct a system that
produces the Fourier transform of the input image
and then transform this again to create the original
image
y x y x y x
F F F F
Fourier Transform
of Input Image
Pg. 25

26. Spatial Filtering – A simple 2 Lens System
• We now have direct access to the image spectra and can
filter it physically with apertures
• The low frequency components (small y x
angular deflection from optical axis)
are contained within the center of the
image spectrum
• Using a circular aperture and blocking
out a portion of spectrum re-creates
the image with the higher frequency
components blocked – low pass filter
Pg. 26

27. Spatial Filtering – A simple 2 Lens System
• http://micro.magnet.fsu.edu/primer/java/digitalimaging/processing/fouriertr
ansform/index.html
• The link above gives many interactive images and spatial filtering
examples
– High pass
• Block out the image spectra around origin
– See high resolution portion of image remain unchanged
– Low pass
• Allow low frequency planes waves (small angles) to pass through the aperture
– Blurs image by removing high frequency plane waves
– Can be used to balance versus higher frequency image noise
– Band Reject
• Find an input image with a periodic grating (Black Knot Fungus)
• Image spectra is periodic
• Band reject the aliases
• Recreate image without grating presents
Pg. 27