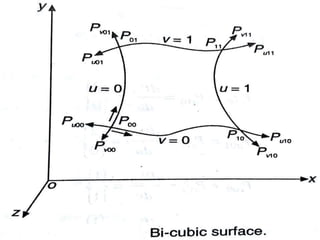
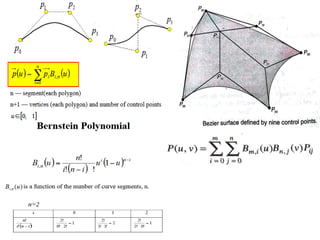
This document discusses two common parametric surface representations: Hermite bi-cubic surfaces and Bezier surfaces. Hermite bi-cubic surfaces connect four corner points and eight tangent vectors at the corners, requiring 16 vectors (48 scalars) to determine the surface coefficients. The parametric equation uses polynomials of the parameters u and v. Bezier surfaces are defined by a set of control points and basic functions of the parameters u and v. The surface passes through the boundary control points but not necessarily through all interior points. Properties include partition of unity and the surface lying within the convex hull of control points.

1. Parametric representation of
synthetic surfaces
1.Hermite Bi-cubic Surface:

3. 1.The parametric bi - cubic surface patch connects four
corner data points and eight tangent vector at the corner
points .
2. Therefore, 16 vectors or 16×3=48 scalars are required to
determine the unknown coefficients in the equation. How?
3. Corner points=4 (P 00 ,P10,P01,P11), corner tangent
vectors=4×2=8, (PU00 , PV00, PU10, PV10 , PU01 , PV01, PU11, PV11)
And corner twist vectors=4. (PUV00 , PUV10, PUV01, PUV11)
4. This surface useful in FEA.
The parametric equation of Hermite bi- cubic equation is
3 3
P(u, v) = ∑∑ai j u i v j , 0 ≤ u ≤ 1, 0≤v ≤1
i = 0 j =0
a i j is POIYNOMIALS CO – EFFICIENTS
u i v j is PARAMETERS

6. The equation can be expanded similar to Hermite cubic curve
where[P] , [P U] , [P V] and [P UV] are the sub –
matrices of the corner points , corner u – tangent
vectors , corner v – tangent vectors and corner
Twist.
The normal vector at N00 is: N00 = Pu00 × P v00
M is Hermite matrix
recall from Hermite curve
U AND V are parameters
of surface patch
B is corner points , corner
uv – Tangent vectors and
corner Twist.

8. Hermite
cubic Curve

11. Hermite curve in
vector form

12. where [MH] is the Hermite matrix and V is the geometry (or
boundary conditions) vector.

13. 2.Bezier surface

14. Bezier curve
• ABezier Curve is obtained by adefining polygon.
• First and last points on the curve are coincident with the firstand last
points of the polygon.
• Degree of polynomial is one lessthan the number ofpoints
• Tangent vectors at the ends of the curve have the samedirections asthe
respective spans
• Thecurve is contained within the convex hull of the definingpolygon

15. Bezier curve
• A Bezier curves is defined by approximating a set of data
points.
• Given n + 1 points (control points) P0+ P1+P2+.....Pn in space,
• The Bezier curve defined by these control points is:
• Where p(u ) is any point on the curve
• Pi is a control points
• B n , i are the Bernstein polynomials
• Where as coefficient are defined as follows :

18. 2.Bezier surface:
1.This is synthetic surface similar to the Bezier curve and it is
obtained by the transformation Bezier curve.
2.It permits twists and kinks or (wrap or loop) in the surface.
3.surface does not pass through all the data points
Definition of Bezier:
1. A two dimensional set of control points P i , j where i is the range of
0 and m , and j is the range of 0 and n .
Thus in this case , we have m+1 rows and n+1 columns of control
points and the control point on the i th row and jth columns are
denoted by P i , j
Note that we have (m + 1) (n + 1) control points in total.

19. •The following is the equation of the Bezier surface defined by m+1
rows and n+ 1 columns of control points:
• Where B m,i (u) and B n,j (v) are the i th and j th
basic functions in the u and v directions
• Recall from the Bezier curves , these basic
functions are defined as follows

20. Figure show Bezier surface defined by the three rows
and three columns and nine control points and hence
is a Bezier surface of degree ( 2 , 2 ).

21. 1. The basic functions of a Bezier surface are the coefficients of control points
2 From the definition, it is clear that these 2-dimensional basis functions are
the product of two one – dimensional Bezier basic functions
3.Basic functions for a Bezier surface are parametric surfaces of two
variables u and v defined on the unit square.
4.Figure shows the basic function for control points P 0, 0 (left) and P 1, 1 (right)
5. For control point P 0, 0 , its basis function is the product of two one –
dimensional Bezier basis functions B 2, 0 (U) in the U- direction and
B 2, 0 (V) in the V - direction as shown in figure (a).
6. Figure (b) shows the basic functions for P 1, 1 , which is the product of B 2, 1 (U)
in the U- direction and B 2, 1 (V) in the V – direction.

22. Properties of Bezier surfaces

23. 3. Partition of unity : The sum of all B m, i (U) B n, j (v) is 1 for all u and v
in the range of 0 and 1. this mean that any pair of u and v in the range
of 0 and 1 , the following holds :
4.Convex hull property: surface p(u,v) lies in the convex
hull defined by its control net.
5.Affine in variance:

24. B- spline surfaces