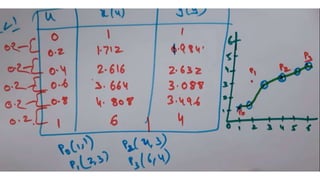
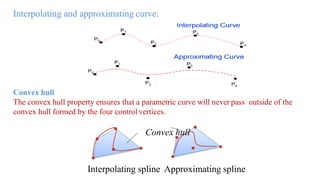
The document covers geometric modeling in mechanical engineering, detailing various techniques such as Hermite curves, Bezier curves, B-spline curves, and solid modeling methods like constructive solid geometry (CSG) and boundary representation (B-rep). It explains the properties and applications of each type of curve and surface used in modeling, emphasizing the advantages of 3D models for simulations, presentations, and manufacturing. Additionally, it discusses the validity and construction methods of solid models, highlighting the differences between CSG and B-rep approaches.

1. TAMIL SELVAN M
Assistant Professor
Department of Mechanical Engineering
KIT-Kalaignarkarunanidhi Institute of Technology
UNIT 2- GEOMETRIC MODELLING

2. UNIT 2- GEOMETRIC MODELLING
Representation of curves- Hermite curve- Bezier curve- B-
spline curves-rational curves-Techniques for surface modeling –
surface patch- Coons and bicubic patches- Bezier and B-spline
surfaces. Solid modeling techniques- CSG andB-rep

3. Geometric modeling
Geometric (3D) models are easier to interpret.
Simulation under real-life conditions.
 Less expensive than building a physicalmodel.
 3 D models can be used to perform finite element analysis
(stress, deflection, thermal)
 3D modelscan be used directlyin manufacturing, Computer
Numerical Control (CNC).
 Can be used for presentations andmarketing.

4. Types of geometric modeling methods
Wireframe modeling
Surface modeling
Solid modeling

5. Wireframe Modeling
Wire-frame modelling uses points and curves(i.e. lines, circles, arcs) to
define objects.
 The user uses edges and vertices of the part to form a 3-Dobject
Wireframe model Part

8. Representation of curves

13. Representation of curves
Types of Curve Equations
•Explicit (non-parametric) Y = f(X), Z = g(X)
•Implicit (non-parametric)
f(X,Y,Z) = 0
•Parametric
X = X(t), Y = Y(t), Z =Z(t)

16. Basic Concepts :
C 2
C 0 - Zero-order parametric continuity - the two curves sections must have
the same coordinate position at the boundary point.
C 1 - First-order parametric continuity - tangent lines of the coordinate
functions for two successive curve sections are equal at their joining point.
C 2 - second-order parametric continuity - both the first and second
parametric derivatives of the two curve sections are the same at the
intersection,

17. Interpolating and approximating curve:
Interpolating spline Approximating spline
Convex hull
The convex hull property ensures that a parametric curve will never pass outside of the
convex hull formed by the four control vertices.
Convex hull

18. Hermite curve

24. Hermite Curve
Hermite curves are designed by using two control points and tangent
segments at each control point

25. Hermite Curve contd…

26. Hermite Curve contd…

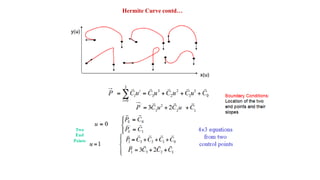
27. Hermite Curve contd…
where [MH] is the Hermite matrix and V is the geometry (or boundary conditions)
vector.

28. Properties:
•The Hermite curve is composed of a linear combinations of tangents and locations (for
each u)
•Alternatively, the curve is a linear combination of Hermite basis functions (the matrix
M)
• The piecewise interpolation scheme is C1 continuous
•The blending functions have local support; changing a control point or a tangent vector,
changes its local neighbourhood while leaving the rest unchanged
Disadvantages:
Requires the specification of the tangents. This information is not always available.
Limited to 3rd degree polynomial therefore the curve is quite stiff .

48. Bezier Curve
• A Bezier Curve is obtained by a defining polygon.
• First and last points on the curve are coincident with the first and last points of
the polygon.
• Degree of polynomial is one less than the number of points
• Tangent vectors at the ends of the curve have the same directions as the
respective spans
• The curve is contained within the convex hull of the defining polygon.

50. Properties Bezier curve
• The Bezier curve starts at P0 and ends at Pn; this is known as ‘endpoint
interpolation’ property.
• The Bezier curve is a straight line when all the control points of a cure are
collinear.
• The beginning of the Bezier curve is tangent to the first portion of the Bezier
polygon.
• A Bezier curve can be divided at any point into two sub curves, each of which is also a
Bezier curve.
• A few curves that look like simple, such as the circle, cannot be expressed accurately by a
Bezier; via four piece cubic Bezier curve can similar a circle, with a maximum radial error
of less than one part in a thousand (Fig.1).
Fig1. Crcular Bezier curve

51. • Each quadratic Bezier curve is become a cubic Bezier curve, and more commonly, each
degree ‘n’ Bezier curve is also a degree ‘m’ curve for any m > n.
• Bezier curves have the different diminishing property. A Bezier curves does not ‘ripple’ more
than the polygon of its control points, and may actually ‘ripple’ less than that.
• Bezier curve is similar with respect to t and (1-t). This represents that the sequence of
control points defining the curve can be changes without modify of the curve shape.
• Bezier curve shape can be edited by either modifying one or more vertices of its
polygon or by keeping the polygon unchanged or simplifying multiple coincident points
at a vertex (Fig .2).
Fig: 2. Bezier curve shpe

60. B-spline Curve
Ni,k(u)'s are B-spline basis functions of degree p.
• The form of a B-spline curve is very similar to that of a Bézier curve. Unlike a Bézier curve, a B-
spline curve involves more information, namely: a set of n+1 control points, a knot vector of
m+1 knots, and a degree p.
• Given n + 1 control points P0, P1, ..., Pn and a knot vector U = { u0, u1, ..., um }, the B-
spline curve of degree p defined by these control points and knot vector.
• The knot points divide a B-spline curve into curve segments, each of which is defined on a
knot span.
m = n + p + 1.
• It provide local control of the curve shape.
• It also provide the ability to add control points without increasing the degree of the curve.
• B-spline curves have the ability to interpolate or approximate a set of given data points.
The B-spline curve defined by n+1 control points Pi is given by

61. • The degree of a Bézier basis function depends on the number of control points.
• To change the shape of a B-spline curve, one can modify one or more of these
control parameters: the positions of control points, the positions of knots, and the
degree of the curve.
• If the knot vector does not have any particular structure, the generated curve will
not touch the first and last legs of the control polyline as shown in the left figure
below.
• This type of B-spline curves is called open B-spline curves.
Properties of B-Spline Curve:

62. The first property ensures that the relationship between the curve and its defining
control points is invariant under affinetransformations.
The second property guarantees that the curve segment lies completely within the
convex hull of Pi.
The third property indicates that each segment of a B-spline curve is influenced by only k
control points or each control point affects only only k curve segments, as shown in Figure 1.
It is useful to notice that the Bernstein polynomial, has the same first two properties
mentioned above.

63. The B-spline function
The B-spline function also has the property of recursion, which is defined as

64. “ A surface model represents the skin of an
object, these skins have no thickness or material type ”
Surface modeling is more sophisticated than wireframe modeling
in that it defines not only the edges of a 3D object, but also its
surfaces.
 I n surface modeling, objects are defined by their bounding faces.
Surface Modeling

65. Surface Entities
Analytic entities include :
• Plane surface,
• Ruled surface,
• Surface of revolution, and
• Tabulated cylinder.
 Synthetic entities include
• Hermite Cubic spline surface,
• B-spline surface,
• Bezier surface, and
• Coons patches.

86. Plane surface

87. Ruled (lofted) surface. This is a linear surface. It interpolates
linearly between two boundary curves that define the surface.

88. Surface of revolution. This is an axisymmetric surface that can
model axisymmetric objects. It is generated by rotating a planar
wireframe entity in space about the axis of symmetry a certain
angle.

89. Tabulated cylinder. This is a surface generated by translating a
planar curve a certain distance along a specified direction (axis of
the cylinder).

90. Bezier surface. This is a surface that approximates given input
data. It is different from the previous surfaces in that it is a synthetic
surface. Similarly to the Bezier curve, it does not pass through all
given data points. It is a general surface that permits, twists, and
kinks . The Bezier surface allows only global control of the surface.

98. B-spline surface. This is a surface that can approximate or
interpolate given input data. It is a synthetic surface. It is a general
surface like the Bezier surface but with the advantage of permitting
local control of the surface.

99. SOLID MODELLING

100. Why solid modeling?
• Recall weakness of wireframe and surface
modeling
– Ambiguous geometric description
– incomplete geometric description
– lack topological information
– Tedious modeling process
– Awkward user interface

101. Solid model
• Solid modeling is based on complete, valid
and unambiguous geometric representation
of physical object.
– Complete points in space can be classified.
(inside/ outside)
– Valid vertices, edges, faces are connected
properly.
– Unambiguous there can only be one
interpretation of object

102. Solid model representation
schemes
1. Constructive solid geometry (CSG)
2. Boundary representation (B-rep)
3. Spatial enumeration
4. Instantiation.

103. Constructive solid geometry (CSG)
• Objects are represented as a combination of
simpler solid objects (primitives).
• The primitives are such as cube, cylinder, cone,
torus, sphere etc.
• Copies or “instances” of these primitive shapes are
created and positioned.
• A complete solid model is constructed by
combining these “instances” using set specific,
logic operations (Boolean)

104. • Boolean operation
– each primitive solid is assumed to be a set of
points, a boolean operation is performed on
point sets and the result is a solid model.
– Boolean operation union, intersection and
difference
– The relative location and orientation of the two
primitives have to be defined before the
boolean operation can be performed.
– Boolean operation can be applied to two solids
other than the primitives.
Constructive solid geometry (CSG)

105. Constructive solid geometry (CSG)-
boolean operation
• Union
– The sum of all points in each of two defined
sets. (logical “OR”)
– Also referred to as Add, Combine, Join, Merge
A B
A  B

106. • Difference
– The points in a source set minus the points
common to a second set. (logical “NOT”)
– Set must share common volume
– Also referred to as subtraction, remove, cut
Constructive solid geometry (CSG)-
boolean operation
A - B
A B

107. • intersection
– Those points common to each of two defined
sets (logical “AND”)
– Set must share common volume
– Also referred to as common, conjoin
Constructive solid geometry (CSG)-
boolean operation
A  B
A B

108. • When using boolean operation, be careful to
avoid situation that do not result in a valid
solid
Constructive solid geometry (CSG)-
boolean operation
A  B
A B

109. • Boolean operation
– Are intuitive to user
– Are easy to use and understand
– Provide for the rapid manipulation of large
amounts of data.
• Because of this, many non-CSG systems
also use Boolean operations
Constructive solid geometry (CSG)-
boolean operation

110. • Data structure does not define model shape
explicitly but rather implies the geometric shape
through a procedural description
– E.g: object is not defined as a set of edges & faces but
by the instruction : union primitive1 with primitive 2
• This procedural data is stored in a data structure
referred to as a CSG tree
• The data structure is simple and stores compact
data easy to manage
Constructive solid geometry (CSG)-
data structure

111. • CSG tree stores the history of applying
boolean operations on the primitives.
– Stores in a binary tree format
– The outer leaf nodes of tree represent the
primitives
– The interior nodes represent the boolean
operations performed.
Constructive solid geometry (CSG)-
CSG tree

112. Constructive solid geometry (CSG)-
CSG tree
+
-

113. • More than one procedure (and hence database) can
be used to arrive at the same geometry.
Constructive solid geometry
(CSG)- not unique

-

114. • CSG representation is unevaluated
– Faces, edges, vertices not defined in explicit
• CSG model are always valid
– Since built from solid elements.
• CSG models are complete and
unambiguous
Constructive solid geometry (CSG)
representation

115. • CSG is powerful with high level command.
• Easy to construct a solid model – minimum
step.
• CSG modeling techniques lead to a concise
database less storage.
– Complete history of model is retained and can
be altered at any point.
• Can be converted to the corresponding
boundary representation.
Constructive solid geometry (CSG) -
advantage

116. • Only boolean operations are allowed in the
modeling process with boolean operation
alone, the range of shapes to be modeled is
severely restricted not possible to construct
unusual shape.
• Requires a great deal of computation to derive the
information on the boundary, faces and edges
which is important for the interactive display/
manipulation of solid.
Constructive solid geometry (CSG) -
disadvantage

117. solution
• CSG representation tends to accompany the
corresponding boundary representation
hybrid representation
• Maintaining consistency between the two
representations is very important.

118. Boundary representation (B-Rep)
• Solid model is defined by their enclosing
surfaces or boundaries. This technique
consists of the geometric information about
the faces, edges and vertices of an object
with the topological data on how these are
connected.

119. Boundary representation (B-Rep)
• Why B-Rep includes such topological
information?
- A solid is represented as a closed space in
3D space (surface connect without gaps)
- The boundary of a solid separates points
inside from points outside solid.

120. B-Rep vs surface modeling
• Surface model
– A collection of surface entities which simply
enclose a volume lacks the connective data to
define a solid (i.e topology).
• B- Rep model
– Technique guarantees that surfaces definitively
divide model space into solid and void, even
after model modification commands.

121. B-Rep data structure
• B-Rep graph store face, edge and vertices
as nodes, with pointers, or branches
between the nodes to indicate connectivity.

122. B-Rep data structure
solid
f3 f2
f4
E3
E4
E5
f5E2E6
E7
E8
v1 v2
v3
f1
E1 v4
v5
vertex1 vertex2 vertex3 vertex4 vertex5
(x, y, z)
face1 face2 face3 face4 face5
Combinatorial
edge1 edge2 edge3 edge4 edge5 edge6 edge7 edge8 structure /
topology
Metric information/
geometry

123. Boundary representation- validity
• System must validate topology of created
solid.
• B-Rep has to fulfill certain conditions to
disallow self-intersecting and open objects
• This condition include
– Each edge should adjoin exactly two faces and
have a vertex at each end.
– Vertices are geometrically described by point
coordinates

124. Boundary representation- validity
• This condition include (cont)
– At least three edges must meet at each vertex.
– Faces are described by surface equations
– The set of faces forms a complete skin of the solid
with no missing parts.
– Each face is bordered by an ordered set of edges
forming a closed loop.
– Faces must only intersect at common edges or
vertices.
– The boundaries of faces do not intersect themselves

125. • Validity also checked through mathematical
evaluation
– Evaluation is based upon Euler’s Law (valid for
simple polyhedra – no hole)
– V – E + F = 2 V-vertices E- edges F- face loops
V = 5, E = 8, F = 5
5 – 8 + 5 = 2
Boundary representation- validity
f3 f2
f4
E3
E4
E5
E7
E8
f5E2E6
v2
v3
f1
E1 v4
v5
v1

126. Boundary representation- validity
• Expanded Euler’s law for complex polyhedrons
(with holes)
• Euler-Poincare Law:
– V-E+F-H=2(B-P)
– H – number of holes in face, P- number of passages or through
holes, B- number of separate bodies.
V = 24, E=36, F=15, H=3,
P=1,B=1

127. • Valid B-Reps are unambiguos
• Not fully unique, but much more so than
CSG
• Potential difference exists in division of
– Surfaces into faces.
– Curves into edges
Boundary representation-
ambiguity and uniqueness

128. • Capability to construct unusual shapes that
would not be possible with the available
CSG aircraft fuselages, swing shapes
• Less computational time to reconstruct the
image
Boundary representation-
advantages

129. • Requires more storage
• More prone to validity failure than CSG
• Model display limited to planar faces and
linear edges
- complex curve and surfaces only approximated
Boundary representation-
disadvantages

130. Solid object construction method
• Sweeping
• Boolean
• Automated filleting and chambering
• Tweaking
– Face of an object is moved in some way

131. Solid Modeling
 I n the solid modeling, the solid definitions include vertices
(nodes), edges, surfaces, weight, and volume. The model
is a complete and unambiguous representation of a
precisely enclosed and filled volume

132. Methods of Creating Solid Models
Constructive Solid Geometry (CSG), CAD packages; Unigraphics, AutoC
– 3D modeler.
Boundary Representation (B-rep), mostly used in finite element programs.
Parametric Modeling, CAD packages: SolidWorks, Pro/Engineer

133. Primitive solids
Primitive creation functions:
 These functions retrieve a
solid of a simple shape
from among the primitive
solids stored in the
program in advance and
create a solid of the same
shape but of the size
specified by the user

134. Boolean Operations
Union
Subtract
Intersection

135. Union
Solid Modeling Example Using CSG
Plan your modeling strategy
before you start creating the
solid model
Cut
Cut