The cubic Hermite spline curve uses a cubic polynomial to interpolate between data points and guarantees continuity of the curve as well as its first and second derivatives at points. It is defined by two endpoints and the tangent vectors at those endpoints. The curve shape can be controlled by changing the endpoints or tangent vectors. The curve is represented parametrically and the coefficients of the polynomial are determined by satisfying boundary conditions at the endpoints.

1. Hermite Cubic Spline Curve
The cubic Hermite spline curves is one of the simplest synthetic curve which is
represented in parametric form. This curve is used to interpolate through the given data
points. It is one form of general parametric cubic spline is popular because it is simple to
compute, provide continuity of the curve, its slope (1st
order derivative) and its curvature
(2nd
order derivative ) at a point. Any curve may be built up of a series of cubic segments.
The general non-parametric equation for the basic 2D cubic spline is-
y=a0 + a1.x +a2.x2
+ a3.x3
This Curve utilizes a cubic equation therefore four conditions are require to determine the
coefficients of the equation, where unknown constants are a0, a1, a2 and a3.These may
be 4 points through which the curve must pass, or 3 points and a slope at any one of
them, or the positions of two end points and two tangent vectors to end points.
The slope equation is
y’=a1 + 2a2.x + 3.a3.x2
and
The curvature equation is
y”=2.a2 + 6.a3.x
Thus for a single segment we will have 4 boundary conditions.
y
u = 1
P’0
P1 P’1
P0 u = 0
x
The parametric form of the cubic spline is given by
P(u) = ∑3
𝑖=0 ai ui
, 0≤u≤1
P(u) = a0 + a1u1
+ a2u2
+ a3u3
Where u is parameter ranging 0 to 1 and a is polynomial coefficients (algebric),
By differentiating with respect to u we get tangent vector to the curve at any point –
P’(u) = a1 + 2a2u + 3a3u2
, 0≤ u ≤ 1
In scaler form this equation is written as
X(u) = aox + a1xu1
+ a2xu2
+ a3xu3
Y(u) = aoy + a1yu1
+ a2yu2
+ a3yu3
Z(u) = aoz + a1zu1
+ a2zu2
+ a3zu3
Applying boundary conditions u=0 and u=1 at both end points, we get following four
equations
At u=0,
P0 = P(0)= a0 and P’0 = P’(0) = a1
At u=1,
P1 = P(1) =a0 + a1 + a2 + a3

2. And
P’1 = P’(1) = a1 + 2a2 + 3a3
Solving above four equations simultaneously we get polynomial coefficient values –
A0 = P0 and a1 = P’0
Put values of a0 and a1 in P1 (at u = 1)
P1 = a0 + a1 + a2 + a3
P1 = P0 + P’0 + a2 + a3 or a2 =p1 – p’0
Put value of a2 in P’1 = a1 + 2a2 + 3a3
P’1 = p’0 + 2(P1-P0-P’0-a3) + 3a3
P’1 = a3 – P’0 + 2p1 – 2p0 or
a3 = 2(P0 – P1) + P’1 + P’0
Now substitute a3 in equation P1 = a0 + a1 + a2 + a3 After substituting polynomial
coefficients in eqn. (8.42)
We get,
P(u) = (2u3
– 3u2
+ 1)P0 + (-2u3
+ 3u2
)P1 + (u3
– 2u2
+u)P’0 + (u3
– u2
)P’1
The above equation can be represented in matrix form as –
P(u) = U.Hm.G, 0≤u≤1
Where U is a parameter u matrix, Hm is the Hermite matrix and G Geometry matrix
(boundary conditions)
Therefore,
P(u) = [ 𝑢3
𝑢2 𝑢 𝑢] . [
2
−3
0
1
−2
3
0
0
1
−2
1
0
1
−1
0
0
] . [
𝑃0
𝑃1
𝑃′0
𝑃′1
]
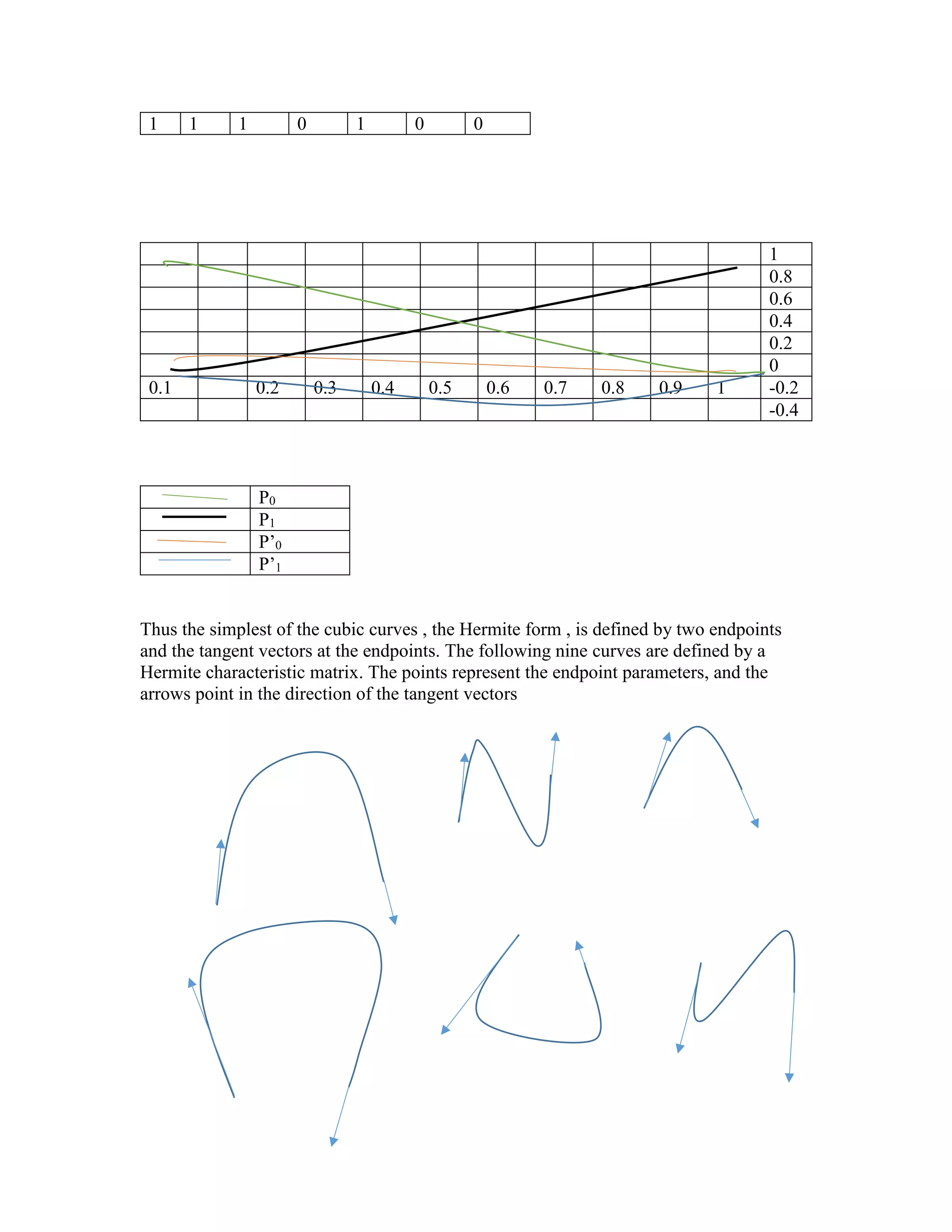
Curve shape can be controlled by changing its end points or its tangent vectors. If the two
points are fixed shape of spline is changed by changing magnitude of the direction of
tangent vectors P’0 andP’1. The hermite blending function are shown
below in the table fig.
U uˆ2 uˆ3 P0 P1 P’0 P’1
0.1 0.01 0.001 0.972 0.028 0.081 -0.009
0.2 0.04 0.008 0.896 0.104 0.128 -0.032
0.3 0.09 0.027 0.784 0.216 0.147 0.063
0.4 0.16 0.064 0.648 0.352 0.144 -0.096
0.5 0.25 0.125 0.5 0.5 0.125 -0.125
0.6 0.36 0.216 0.352 0.684 0.096 -0.144
0.7 0.49 0.343 0.216 0.784 0.063 -0.147
0.8 0.64 0.512 0.104 0.896 0.032 -0.128
0.9 0.91 0.729 0.028 0.972 0.009 -0.081

3. 1 1 1 0 1 0 0
1
0.8
0.6
0.4
0.2
0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 -0.2
-0.4
P0
P1
P’0
P’1
Thus the simplest of the cubic curves , the Hermite form , is defined by two endpoints
and the tangent vectors at the endpoints. The following nine curves are defined by a
Hermite characteristic matrix. The points represent the endpoint parameters, and the
arrows point in the direction of the tangent vectors

4. Fig. Hermite Curve
Drawbacks
1) Due to its global control characteristics , by changing the position of a data point
the entire shape of spline changes.
2) The curve is always cubic regardless of the number of data points.
3) The curve is less smoother than any other synthetic curves.
4) Practically the direction and magnitude of the tangent vector is very difficult to
know.
5) More intuitive to only specify points.
EXAMPLE:-
Find the equation of Hermite Cubic spline which defined by end points P0(0,0) ,
P1(3,0) with tangent vectors P’0(1,1) , P’1(1,1). Also calculate intermediate point at
u=1/2 and u=2/3.
GIVEN:
P0(0,0) , P1(3,0) , P’0(1,1) , P’1(1,1)
We know for Hermite Cubic spline , P(u) = U.Hm.G, 0≤u≤1
Therefore,

5. P(u) = [ 𝑢3
𝑢2
𝑢 1].[
2
−3
0
1
−2
3
0
0
1
−2
1
0
1
−1
0
0
] . [
𝑃0
𝑃1
𝑃′0
𝑃′1
]
P(u) = [ 𝑢3
𝑢2
𝑢 1]. [
2
−3
0
1
−2
3
0
0
1
−2
1
0
1
−1
0
0
] . [
0
3
1
1
0
0
1
1
0
0
0
0
]
P(u) = [ 𝑢3
𝑢2
𝑢 1]. [
−4
5
1
0
2
−3
1
0
0
0
0
0
]
Thus the parametric equation of cubic spline is given by,
P(u) = [(-4*u3
+ 5*u2
+ u)(2*u3
– 3*u2
+ u) 0 ]
At u = ½
P(u)= [(-4*(o.5)3
+ 5*(0.5)2
+ (0.5))(2*(0.5)3
– 3*(0.5)2
+ (0.5)) 0]
P(u)=[1.5 0 0]
At u =2/3
P(u)= [(-4*(2/3)3
+ 5*(2/3)2
+ (2/3))(2.(2/3)3
– 3*(2/3)2
+ (2/3)) 0]
P(u)=[1.7 -0.07 0]
Concentration of Multiple Cubic Spline Segments
To concenteenate n curve segments we need n+1 series of points and requires 4.n
coefficients. For example , let us consider two curve segments PQ and QR with
P(0,10), Q(10,20), R(20,30),P’=-1 and R’=1. Here n=2 therefore number of points
will be n+1=3 and require to evaluate 4.n = 8 coefficients.
In scalar form parametric equation for segment PQ is written as –
XPQ(u) = a0 + a1.u + a2.u2
+ a3.u3
and
YPQ(u) = a0 + a1.u + a2.u2
+ a3.u3
0≤u≤1
And for segment Q is written as
XQR(u) = b0 + b1.u + b2.u2
+ b3.u3
and
YQR(u) = b0 + b1.u + b2.u2
+ b3.u3
0≤u≤1
The slope equation is—
X’(u) = a1 + 2.a2 + 3.a3.u2
and
Y’(u) = a1 + 2.a2.u +3.a3.u2
, 0≤u≤1
And the curvature equation is---
Y”(u) = 2.a2 + 6.a3.u
For segment PQ we have , at P,x=0 and y=10 and y’=-1
Then
YPQ(0) = a0 + a1.u + a2.u2
+ a3.u3
= a0