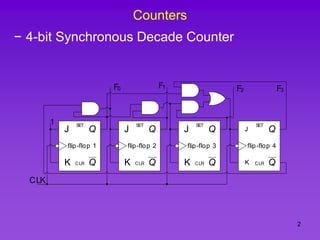
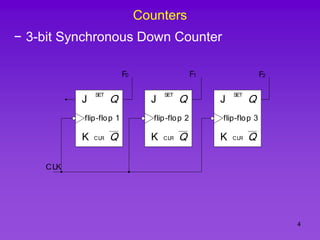
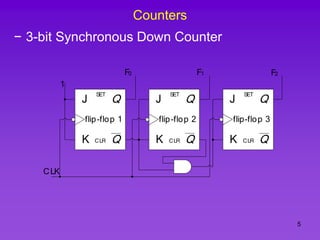
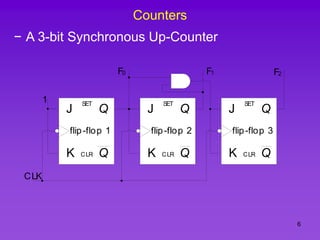
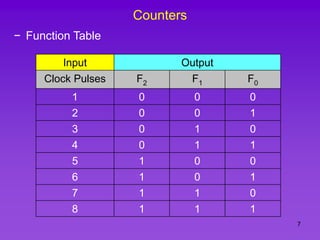
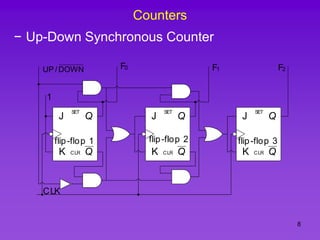
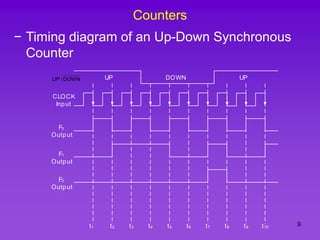
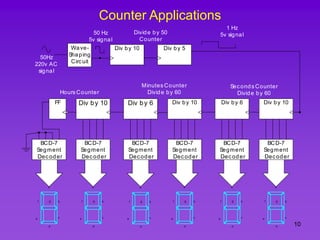
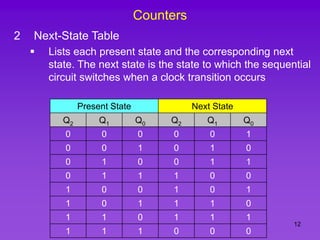
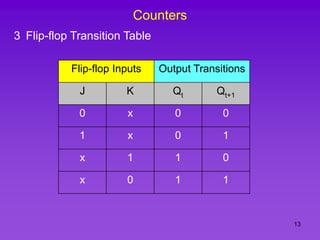
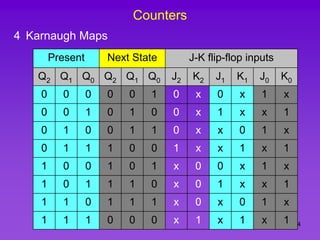
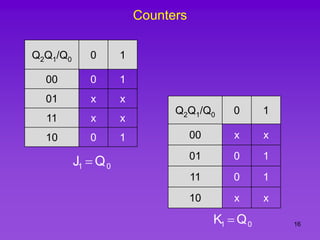
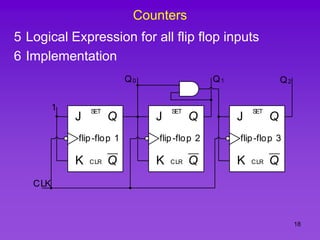
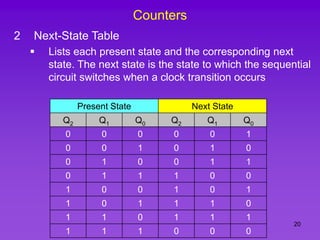
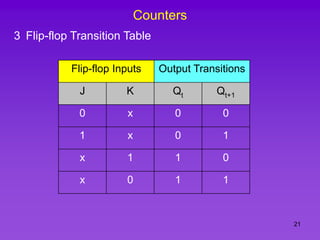
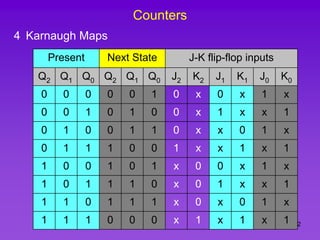
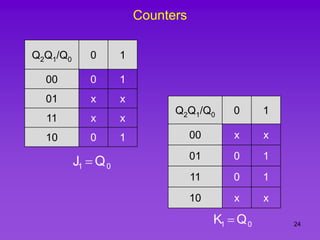
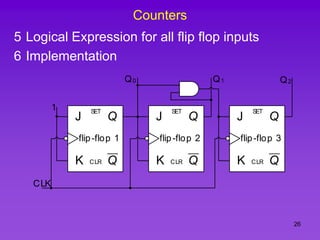
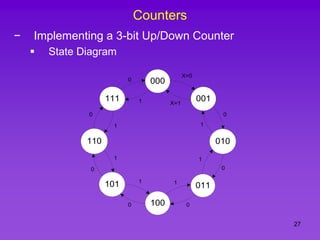
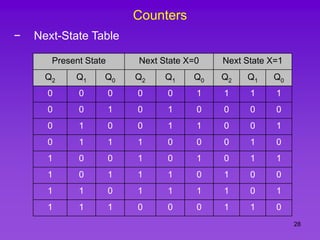
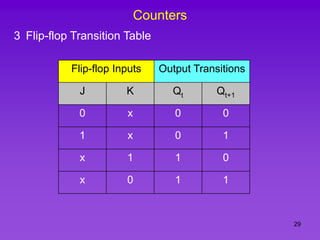
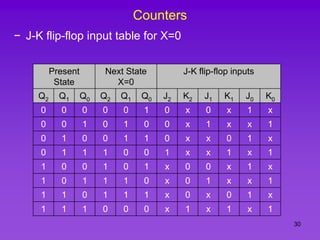
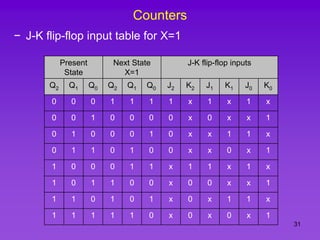
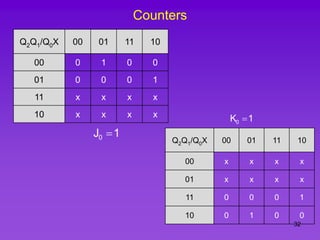
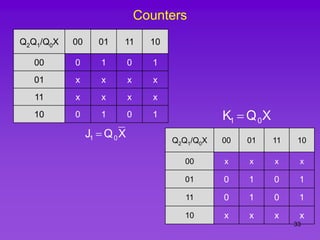
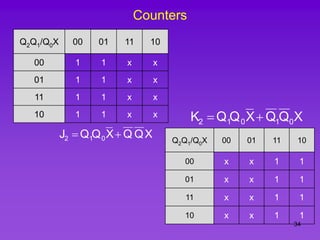
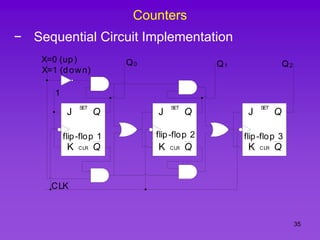
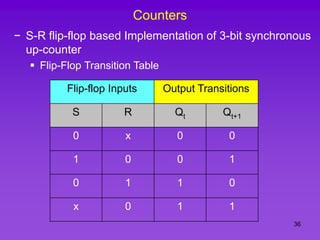
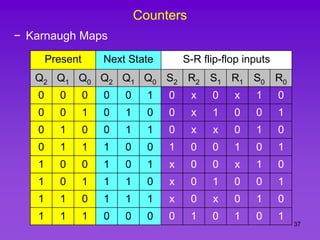
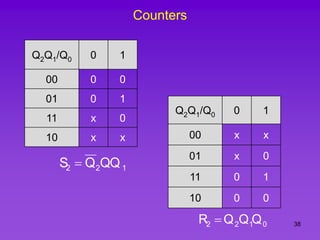
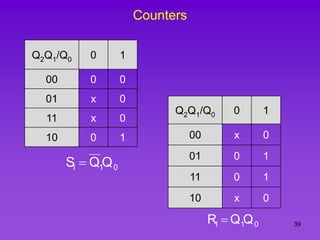
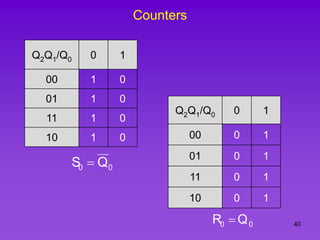
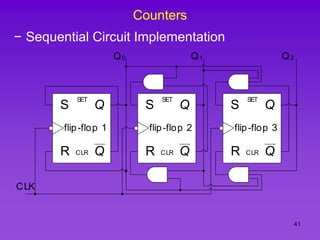
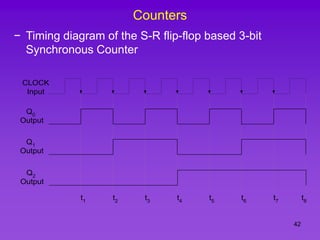
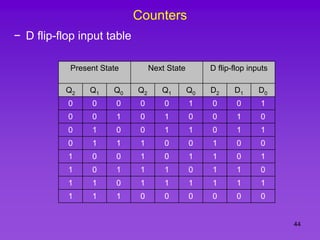
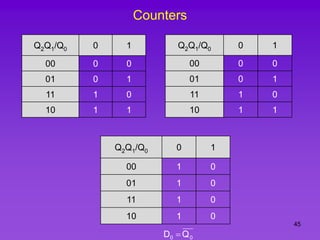
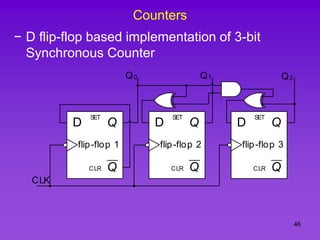
The document provides detailed information on computer logic and design, specifically focusing on various types of counters, including 4-bit synchronous decade counters and 3-bit synchronous up/down counters. It includes timing diagrams, state diagrams, next-state tables, and implementation details using flip-flops, along with Karnaugh maps for logical expressions. The content is structured to aid in understanding the sequential circuit design and applications of these counters in digital systems.

1. 1
Computer Logic & Design
Fall 2005
t0 t4 t5 t6
t1 t2 t3
A
B
F
Sana Ullah Qaisar
Lecturer, Telecom. Engineering
NUCES, Islamabad

2. 2
Counters
− 4-bit Synchronous Decade Counter
J
Q
Q
K
SET
CLR
flip-flop 1
CLK
J
Q
Q
K
SET
CLR
flip-flop 2
J
Q
Q
K
SET
CLR
flip-flop 3
J
Q
Q
K
SET
CLR
flip-flop 4
1
F0 F1 F2 F3

3. 3
Counters
− Timing diagram of a Synchronous Decade
Counter
CLOCK
Input
F0
Output
F1
Output
t1 t2 t3 t4 t5 t6 t7 t8
F2
Output
F3
Output
t9 t10

4. 4
Counters
− 3-bit Synchronous Down Counter
J
Q
Q
K
SET
CLR
flip-flop 1
CLK
J
Q
Q
K
SET
CLR
flip-flop 2
J
Q
Q
K
SET
CLR
flip-flop 3
F0 F1 F2

5. 5
Counters
− 3-bit Synchronous Down Counter
J
Q
Q
K
SET
CLR
flip-flop 1
1
CLK
J
Q
Q
K
SET
CLR
flip-flop 2
J
Q
Q
K
SET
CLR
flip-flop 3
F0 F1 F2

6. 6
Counters
− A 3-bit Synchronous Up-Counter
J
Q
Q
K
SET
CLR
flip-flop 1
1
CLK
J
Q
Q
K
SET
CLR
flip-flop 2
J
Q
Q
K
SET
CLR
flip-flop 3
F0 F1 F2

7. 7
Counters
− Function Table
Input Output
Clock Pulses F2 F1 F0
1 0 0 0
2 0 0 1
3 0 1 0
4 0 1 1
5 1 0 0
6 1 0 1
7 1 1 0
8 1 1 1

8. 8
Counters
− Up-Down Synchronous Counter
J
Q
Q
K
SET
CLR
flip-flop 1
1
CLK
J
Q
Q
K
SET
CLR
flip-flop 2
J
Q
Q
K
SET
CLR
flip-flop 3
F0 F1 F2
DOWN
/
UP

9. 9
Counters
− Timing diagram of an Up-Down Synchronous
Counter
CLOCK
Input
F0
Output
F1
Output
t1 t2 t3 t4 t5 t6 t7 t8
F2
Output
t9 t10
UP DOWN UP
DOWN
/
UP

10. 10
Counter Applications
Div by 10
Div by 6
Div by 10
Div by 6
Div by 10
FF
Div by 5
Div by 10
BCD-7
Segment
Decoder
a
b
c
d
e
f g
BCD-7
Segment
Decoder
a
b
c
d
e
f g
BCD-7
Segment
Decoder
a
b
c
d
e
f g
BCD-7
Segment
Decoder
a
b
c
d
e
f g
BCD-7
Segment
Decoder
a
b
c
d
e
f g
BCD-7
Segment
Decoder
a
b
c
d
e
f g
Wave-
Shaping
Circuit
50Hz
220v AC
signal
50 Hz
5v signal
1 Hz
5v signal
Seconds Counter
Divide by 60
Minutes Counter
Divide by 60
Hours Counter
Divide by 50
Counter

11. 11
Counters
1 State Diagram
 A sequential circuit (state machine) is described
by a state diagram, which shows the sequence
of state through which the sequential circuit
progresses when it is clocked
 State diagram of a 3-bit Up-Counter
111
110
011
001
000
101
010
100

12. 12
Counters
2 Next-State Table
 Lists each present state and the corresponding next
state. The next state is the state to which the sequential
circuit switches when a clock transition occurs
Present State Next State
Q2 Q1 Q0 Q2 Q1 Q0
0 0 0 0 0 1
0 0 1 0 1 0
0 1 0 0 1 1
0 1 1 1 0 0
1 0 0 1 0 1
1 0 1 1 1 0
1 1 0 1 1 1
1 1 1 0 0 0

13. 13
Counters
3 Flip-flop Transition Table
Flip-flop Inputs Output Transitions
J K Qt Qt+1
0 x 0 0
1 x 0 1
x 1 1 0
x 0 1 1

14. 14
Counters
4 Karnaugh Maps
Present Next State J-K flip-flop inputs
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1 J0 K0
0 0 0 0 0 1 0 x 0 x 1 x
0 0 1 0 1 0 0 x 1 x x 1
0 1 0 0 1 1 0 x x 0 1 x
0 1 1 1 0 0 1 x x 1 x 1
1 0 0 1 0 1 x 0 0 x 1 x
1 0 1 1 1 0 x 0 1 x x 1
1 1 0 1 1 1 x 0 x 0 1 x
1 1 1 0 0 0 x 1 x 1 x 1

15. 15
Counters
Q2Q1/Q0 0 1
00 0 0
01 0 1
11 x x
10 x x
0
1
2 Q
Q
J 
Q2Q1/Q0 0 1
00 X X
01 X X
11 0 1
10 0 0
0
1
2 Q
Q
K 

16. 16
Counters
Q2Q1/Q0 0 1
00 0 1
01 x x
11 x x
10 0 1
0
1 Q
J 
Q2Q1/Q0 0 1
00 x x
01 0 1
11 0 1
10 x x
0
1 Q
K 

17. 17
Counters
Q2Q1/Q0 0 1
00 1 x
01 1 x
11 1 x
10 1 x
1
J0 
Q2Q1/Q0 0 1
00 x 1
01 x 1
11 x 1
10 x 1
1
K0 

18. 18
Counters
5 Logical Expression for all flip flop inputs
6 Implementation
J
Q
Q
K
SET
CLR
flip-flop 1
1
CLK
J
Q
Q
K
SET
CLR
flip-flop 2
J
Q
Q
K
SET
CLR
flip-flop 3
Q0 Q1 Q2

19. 19
Counters
1 State Diagram
 A sequential circuit (state machine) is described
by a state diagram, which shows the sequence
of state through which the sequential circuit
progresses when it is clocked
 State diagram of a 3-bit Up-Counter
111
110
011
001
000
101
010
100

20. 20
Counters
2 Next-State Table
 Lists each present state and the corresponding next
state. The next state is the state to which the sequential
circuit switches when a clock transition occurs
Present State Next State
Q2 Q1 Q0 Q2 Q1 Q0
0 0 0 0 0 1
0 0 1 0 1 0
0 1 0 0 1 1
0 1 1 1 0 0
1 0 0 1 0 1
1 0 1 1 1 0
1 1 0 1 1 1
1 1 1 0 0 0

21. 21
Counters
3 Flip-flop Transition Table
Flip-flop Inputs Output Transitions
J K Qt Qt+1
0 x 0 0
1 x 0 1
x 1 1 0
x 0 1 1

22. 22
Counters
4 Karnaugh Maps
Present Next State J-K flip-flop inputs
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1 J0 K0
0 0 0 0 0 1 0 x 0 x 1 x
0 0 1 0 1 0 0 x 1 x x 1
0 1 0 0 1 1 0 x x 0 1 x
0 1 1 1 0 0 1 x x 1 x 1
1 0 0 1 0 1 x 0 0 x 1 x
1 0 1 1 1 0 x 0 1 x x 1
1 1 0 1 1 1 x 0 x 0 1 x
1 1 1 0 0 0 x 1 x 1 x 1

23. 23
Counters
Q2Q1/Q0 0 1
00 0 0
01 0 1
11 x x
10 x x
0
1
2 Q
Q
J 
Q2Q1/Q0 0 1
00 X X
01 X X
11 0 1
10 0 0
0
1
2 Q
Q
K 

24. 24
Counters
Q2Q1/Q0 0 1
00 0 1
01 x x
11 x x
10 0 1
0
1 Q
J 
Q2Q1/Q0 0 1
00 x x
01 0 1
11 0 1
10 x x
0
1 Q
K 

25. 25
Counters
Q2Q1/Q0 0 1
00 1 x
01 1 x
11 1 x
10 1 x
1
J0 
Q2Q1/Q0 0 1
00 x 1
01 x 1
11 x 1
10 x 1
1
K0 

26. 26
Counters
5 Logical Expression for all flip flop inputs
6 Implementation
J
Q
Q
K
SET
CLR
flip-flop 1
1
CLK
J
Q
Q
K
SET
CLR
flip-flop 2
J
Q
Q
K
SET
CLR
flip-flop 3
Q0 Q1 Q2

27. 27
Counters
− Implementing a 3-bit Up/Down Counter
 State Diagram
111
110
011
001
000
101
010
100
X=0
X=1
0
0
0
0
0
0
0
1
1
1
1
1
1
1

28. 28
Counters
− Next-State Table
Present State Next State X=0 Next State X=1
Q2 Q1 Q0 Q2 Q1 Q0 Q2 Q1 Q0
0 0 0 0 0 1 1 1 1
0 0 1 0 1 0 0 0 0
0 1 0 0 1 1 0 0 1
0 1 1 1 0 0 0 1 0
1 0 0 1 0 1 0 1 1
1 0 1 1 1 0 1 0 0
1 1 0 1 1 1 1 0 1
1 1 1 0 0 0 1 1 0

29. 29
Counters
3 Flip-flop Transition Table
Flip-flop Inputs Output Transitions
J K Qt Qt+1
0 x 0 0
1 x 0 1
x 1 1 0
x 0 1 1

30. 30
Counters
− J-K flip-flop input table for X=0
Present
State
Next State
X=0
J-K flip-flop inputs
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1 J0 K0
0 0 0 0 0 1 0 x 0 x 1 x
0 0 1 0 1 0 0 x 1 x x 1
0 1 0 0 1 1 0 x x 0 1 x
0 1 1 1 0 0 1 x x 1 x 1
1 0 0 1 0 1 x 0 0 x 1 x
1 0 1 1 1 0 x 0 1 x x 1
1 1 0 1 1 1 x 0 x 0 1 x
1 1 1 0 0 0 x 1 x 1 x 1

31. 31
Counters
− J-K flip-flop input table for X=1
Present
State
Next State
X=1
J-K flip-flop inputs
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1 J0 K0
0 0 0 1 1 1 1 x 1 x 1 x
0 0 1 0 0 0 0 x 0 x x 1
0 1 0 0 0 1 0 x x 1 1 x
0 1 1 0 1 0 0 x x 0 x 1
1 0 0 0 1 1 x 1 1 x 1 x
1 0 1 1 0 0 x 0 0 x x 1
1 1 0 1 0 1 x 0 x 1 1 x
1 1 1 1 1 0 x 0 x 0 x 1

32. 32
Counters
Q2Q1/Q0X 00 01 11 10
00 0 1 0 0
01 0 0 0 1
11 x x x x
10 x x x x
1
J0 
Q2Q1/Q0X 00 01 11 10
00 x x x x
01 x x x x
11 0 0 0 1
10 0 1 0 0
1
K0 

33. 33
Counters
Q2Q1/Q0X 00 01 11 10
00 0 1 0 1
01 x x x x
11 x x x x
10 0 1 0 1
X
Q
J 0
1  Q2Q1/Q0X 00 01 11 10
00 x x x x
01 0 1 0 1
11 0 1 0 1
10 x x x x
X
Q
K 0
1 

34. 34
Counters
Q2Q1/Q0X 00 01 11 10
00 1 1 x x
01 1 1 x x
11 1 1 x x
10 1 1 x x
X
Q
Q
X
Q
Q
J 0
1
2 
 Q2Q1/Q0X 00 01 11 10
00 x x 1 1
01 x x 1 1
11 x x 1 1
10 x x 1 1
X
Q
Q
X
Q
Q
K 0
1
0
1
2 


35. 35
Counters
− Sequential Circuit Implementation
J
Q
Q
K
SET
CLR
flip-flop 1
1
CLK
J
Q
Q
K
SET
CLR
flip-flop 2
J
Q
Q
K
SET
CLR
flip-flop 3
Q0 Q1 Q2
X=0 (up)
X=1 (down)

36. 36
Counters
− S-R flip-flop based Implementation of 3-bit synchronous
up-counter
 Flip-Flop Transition Table
Flip-flop Inputs Output Transitions
S R Qt Qt+1
0 x 0 0
1 0 0 1
0 1 1 0
x 0 1 1

37. 37
Counters
− Karnaugh Maps
Present Next State S-R flip-flop inputs
Q2 Q1 Q0 Q2 Q1 Q0 S2 R2 S1 R1 S0 R0
0 0 0 0 0 1 0 x 0 x 1 0
0 0 1 0 1 0 0 x 1 0 0 1
0 1 0 0 1 1 0 x x 0 1 0
0 1 1 1 0 0 1 0 0 1 0 1
1 0 0 1 0 1 x 0 0 x 1 0
1 0 1 1 1 0 x 0 1 0 0 1
1 1 0 1 1 1 x 0 x 0 1 0
1 1 1 0 0 0 0 1 0 1 0 1

38. 38
Counters
Q2Q1/Q0 0 1
00 0 0
01 0 1
11 x 0
10 x x
1
2
2 QQ
Q
S 
Q2Q1/Q0 0 1
00 x x
01 x 0
11 0 1
10 0 0
0
1
2
2 Q
Q
Q
R 

39. 39
Counters
Q2Q1/Q0 0 1
00 0 0
01 x 0
11 x 0
10 0 1
0
1
1 Q
Q
S 
Q2Q1/Q0 0 1
00 x 0
01 0 1
11 0 1
10 x 0
0
1
1 Q
Q
R 

40. 40
Counters
Q2Q1/Q0 0 1
00 1 0
01 1 0
11 1 0
10 1 0
0
0 Q
S 
Q2Q1/Q0 0 1
00 0 1
01 0 1
11 0 1
10 0 1
0
0 Q
R 

41. 41
Counters
− Sequential Circuit Implementation
Q
Q
SET
CLR
S
R
flip-flop 1
CLK
Q
Q
SET
CLR
S
R
flip-flop 2
Q
Q
SET
CLR
S
R
flip-flop 3
Q0 Q1 Q2

42. 42
Counters
− Timing diagram of the S-R flip-flop based 3-bit
Synchronous Counter
CLOCK
Input
Q0
Output
Q1
Output
t1 t2 t3 t4 t5 t6 t7 t8
Q2
Output

43. 43
Counters
− Flip-Flop Transition Table
Flip-flop Inputs Output Transitions
D Qt+1
1 1
0 0

44. 44
Counters
− D flip-flop input table
Present State Next State D flip-flop inputs
Q2 Q1 Q0 Q2 Q1 Q0 D2 D1 D0
0 0 0 0 0 1 0 0 1
0 0 1 0 1 0 0 1 0
0 1 0 0 1 1 0 1 1
0 1 1 1 0 0 1 0 0
1 0 0 1 0 1 1 0 1
1 0 1 1 1 0 1 1 0
1 1 0 1 1 1 1 1 1
1 1 1 0 0 0 0 0 0

45. 45
Counters
Q2Q1/Q0 0 1
00 0 0
01 0 1
11 1 0
10 1 1
Q2Q1/Q0 0 1
00 1 0
01 1 0
11 1 0
10 1 0
Q2Q1/Q0 0 1
00 0 0
01 0 1
11 1 0
10 1 1
0
0 Q
D 

46. 46
Counters
− D flip-flop based implementation of 3-bit
Synchronous Counter
Q
Q
SET
CLR
D
flip-flop 1
CLK
Q
Q
SET
CLR
D
flip-flop 2
Q
Q
SET
CLR
D
flip-flop 3
Q0 Q1 Q2