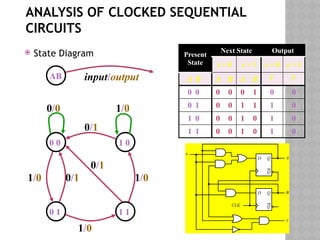
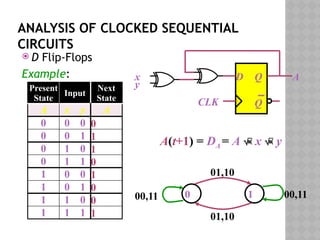
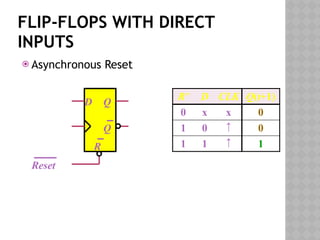
The document discusses synchronous sequential logic in digital logic design, focusing on the function and utility of flip-flops with asynchronous inputs, specifically preset and clear commands. It covers the analysis of clocked sequential circuits, including state equations, transition tables, and state diagrams, illustrating the interactions between present state, input, next state, and output. Examples using D flip-flops are provided to demonstrate how inputs affect the state transitions in digital circuits.

1. DIGITAL LOGIC
DESIGN (DLD)
EE-208412

2. CHAPTER:05
Synchronous Sequential Logic

3. DIRECT INPUTS
 Some flip flops have asynchronous inputs
that are used to force the flip flop to a
particular state independent of the clock
 The input that sets the flip flop to 1 is called
preset or direct set
 The input that clears the flip flop to 0 is called
clear or direct reset
 The direct inputs are useful for bringing all
flip flops in a system to a known starting
state

4. FLIP-FLOPS WITH DIRECT
INPUTS
 Asynchronous Reset
D Q
Q
R
Reset
R’ D CLK Q(t+1)
0 x x 0

5. FLIP-FLOPS WITH DIRECT
INPUTS
 Asynchronous Reset
D Q
Q
R
Reset
R’ D CLK Q(t+1)
0 x x 0
1 0 ↑ 0
1 1 ↑ 1

6. ANALYSIS OF CLOCKED SEQUENTIAL
CIRCUITS
 The State
 State = Values of all Flip-Flops
Example
A B = 0 0
D Q
Q
CLK
D Q
Q
A
B
y
x

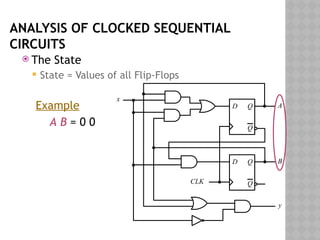
7. ANALYSIS OF CLOCKED SEQUENTIAL
CIRCUITS
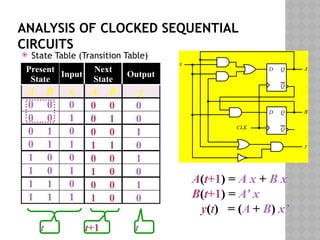
 State Equations
D Q
Q
CLK
D Q
Q
A
B
y
x
A(t+1) = DA
= A(t) x(t)+B(t) x(t)
= A x + B x
B(t+1) = DB
= A’(t) x(t)
= A’ x
y(t) = [A(t)+ B(t)] x’(t)
= (A + B) x’

8. ANALYSIS OF CLOCKED SEQUENTIAL
CIRCUITS
 State Table (Transition Table)
D Q
Q
CLK
D Q
Q
A
B
y
x
A(t+1) = A x + B x
B(t+1) = A’ x
y(t) = (A + B) x’
Present
State
Input
Next
State
Output
A B x A B y
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
t+1 t
t
0 0 0
0 1 0
0 0 1
1 1 0
0 0 1
1 0 0
0 0 1
1 0 0

9. ANALYSIS OF CLOCKED SEQUENTIAL
CIRCUITS
 State Table (Transition Table)
D Q
Q
CLK
D Q
Q
A
B
y
x
A(t+1) = A x + B x
B(t+1) = A’ x
y(t) = (A + B) x’
Present
State
Next State Output
x = 0 x = 1 x = 0 x = 1
A B A B A B y y
0 0 0 0 0 1 0 0
0 1 0 0 1 1 1 0
1 0 0 0 1 0 1 0
1 1 0 0 1 0 1 0
t+1 t
t

10. ANALYSIS OF CLOCKED SEQUENTIAL
CIRCUITS
 State Diagram Present
State
Next State Output
x = 0 x = 1 x = 0 x = 1
A B A B A B y y
0 0 0 0 0 1 0 0
0 1 0 0 1 1 1 0
1 0 0 0 1 0 1 0
1 1 0 0 1 0 1 0
D Q
Q
CLK
D Q
Q
A
B
y
x
0 0 1 0
0 1 1 1
0/0
0/1
1/0
1/0
1/0
1/0 0/1
0/1
AB input/output

11. ANALYSIS OF CLOCKED SEQUENTIAL
CIRCUITS
 D Flip-Flops
Example: D Q
Q
x
CLK
y
A
Present
State
Input
Next
State
A x y A
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0
1
1
0
1
0
0
1
0 1
00,11 00,11
01,10
01,10
A(t+1) = DA = A  x  y