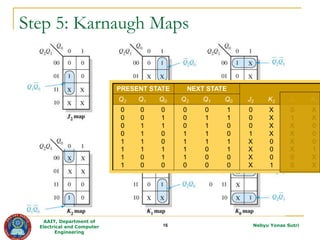
The document describes the steps to design a synchronous counter using sequential logic circuits. It begins with defining the learning outcomes as being able to design a counter through 7 steps: 1) state diagram, 2) next-state table, 3) flip-flop transition table, 4) circuit excitation table, 5) Karnaugh maps, 6) logic expressions, and 7) implementation. It then provides examples working through each step to design a 3-bit Gray code counter using J-K flip-flops. Exercises are provided to design additional counters.

1. Addis Ababa Institute of Technology
(AAIT) Department of Electrical and
Computer Engineering
ECEG-3201 Digital Logic Design

2. AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri2
Learning Outcomes
 At the end of the lecture, students should be able to:
 Design a synchronous counter for any count sequence
using the following steps:
 Step 1: State diagram
 Step 2: Next-state table
 Step 3: Flip-flop transition table
 Step 4: Circuit excitation table
 Step 5: Karnaugh maps
 Step 6: Logic expression for the flip-flop inputs
 Step 7: Counter implementation

3. 3
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Synchronous Counter
 The counter have a fixed time relationship with
each other and generally count at the same time.
 A synchronous counter is one which all the
flip-flops are connected to the same clock.

4. 4
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Sequential Circuits
 Depends on a clock signal and goes through
a set of sequence of states.
 Also called State Machines.
 A counter is a type of sequential circuit.
 Consists of combinational logic section and
memory section.

5. 5
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Sequential Circuits

6. 6
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Sequential Circuit Design Procedures
 The 7 steps in sequential circuit design are:
 Step 1: State diagram
 Step 2: Next-state table
 Step 3: Flip-flop transition table
 Step 4: Circuit excitation table
 Step 5: Karnaugh maps
 Step 6: Logic expression for the flip-flop inputs
 Step 7: Counter Implementation

7. 7
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 1: The State Diagram
 A state machine is described by a state diagram.
 It shows the progression of states in the state
machine.
 E.g: 3-bit Gray code counter:

8. 8
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 2: Next-State Table
 Lists each state along with the corresponding next
state.
 Next state – state that the counter goes to from its
present state upon application of clock pulse.
 E.g: 3-bit Gray code counter
PRESENT STATE NEXT STATE
Q2 Q1 Q0 Q2 Q1 Q0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0

9. 9
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 3: Flip-Flop Transition Table
 To derive the transition table of the J-K flip-flop, let’s
examine the possible transitions:
 0  0
 FF is in RESET mode: J = K =
 FF is in No Change mode: J = K =
 0  0 happens when: J = K =
 0  1
 FF is in SET mode: J = K =
 FF is in Toggle mode: J = K =
 0  1 happens when: J = K =
 1  0
 FF is in RESET mode: J = K =
 FF is in Toggle mode: J = K =
 1  0 happens when: J = K =
0 1
0 0
0 X
01
1 1
1 X
0 1
1 1
1X

10. 10
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 3: Flip-Flop Transition Table
 1  1
 FF is in SET mode: J = 1, K = 0
 FF is in No change mode: J = 0, K = 0
 1  1 happens when: J = X, K = 0
 The J-K transition (or excitation) table is:
OUTPUT TRANSITIONS FLIP-FLOP INPUTS
Q Q+ J K
0
0
1
1




0
1
0
1
0 X
1 X
X 1
X 0

11. 11
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 4: Circuit Excitation Table
 Derived from the next-state table and flip-flop
transition table:
 E.g. 3-bit Gray code counter
PRESENT STATE NEXT STATE Excitation Inputs
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1 J0 K0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
0
1
X
X
X
X
X
X
X
X
0
0
0
1
0
1
X
X
X
X
0
0
X
X
0
0
0
1
X
X
1
X
X
0
1
X
X
0
X
0
1
X
X
0
1
X
OUTPUT TRANSITIONS FLIP-FLOP INPUTS
Q Q+ J K
0
0
1
1




0
1
0
1
0 X
1 X
X 1
X 0

12. 12
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 4: Circuit Excitation Table
 Derived from the next-state table and flip-flop
transition table:
 E.g. 3-bit Gray code counter
PRESENT STATE NEXT STATE Excitation Inputs
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1 J0 K0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
0
1
X
X
X
X
X
X
X
X
0
0
0
1
0
1
X
X
X
X
0
0
X
X
0
0
0
1
X
X
1
X
X
0
1
X
X
0
X
0
1
X
X
0
1
X
OUTPUT TRANSITIONS FLIP-FLOP INPUTS
Q Q+ J K
0
0
1
1




0
1
0
1
0 X
1 X
X 1
X 0

13. 13
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 4: Circuit Excitation Table
 Derived from the next-state table and flip-flop
transition table:
 E.g. 3-bit Gray code counter
PRESENT STATE NEXT STATE Excitation Inputs
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1 J0 K0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
0
1
X
X
X
X
X
X
X
X
0
0
0
1
0
1
X
X
X
X
0
0
X
X
0
0
0
1
X
X
1
X
X
0
1
X
X
0
X
0
1
X
X
0
1
X
OUTPUT TRANSITIONS FLIP-FLOP INPUTS
Q Q+ J K
0
0
1
1




0
1
0
1
0 X
1 X
X 1
X 0

14. 14
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 4: Circuit Excitation Table
 Derived from the next-state table and flip-flop
transition table:
 E.g. 3-bit Gray code counter
PRESENT STATE NEXT STATE Excitation Inputs
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1 J0 K0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
0
1
X
X
X
X
X
X
X
X
0
0
0
1
0
1
X
X
X
X
0
0
X
X
0
0
0
1
X
X
1
X
X
0
1
X
X
0
X
0
1
X
X
0
1
X

15. 15
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 5: Karnaugh Maps

16. 16
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 5: Karnaugh Maps
PRESENT STATE NEXT STATE
Q2 Q1 Q0 Q2 Q1 Q0 J2 K2 J1 K1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
0
1
X
X
X
X
X
X
X
X
0
0
0
1
0
1
X
X
X
X
0
0
X
X
0
0
0
1
X
X

17. 17
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 5: Karnaugh Maps

18. 18
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 6: Logic Expression for Flip-Flop
Inputs
 Derive the logic expression for the flip-flop
inputs from K-map simplification.
 E.g. 3-bit Gray code counter
012
012
021
021
1212120
1212120
QQK
QQJ
QQK
QQJ
QQQQQQK
QQQQQQJ







19. 19
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Step 7: Circuit Implementation
 From the expressions for the J and K inputs,
we get the counter implementation.

20. 20
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
Exercise
 Design a 3-bit Gray code counter using D-flip flops
PRESENT STATE NEXT STATE Excitation Inputs
Q2 Q1 Q0 Q2 Q1 Q0 D2 D1 D0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0

21. 21
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
K-Map Simplification
0 1
00 0 0
01 1 0
11 1 1
10 0 1
Q2Q1
Q0 0 1
00 0 1
01 1 1
11 1 0
10 0 0
Q2Q1
Q0 0 1
00 1 1
01 0 0
11 1 1
10 0 0
Q2Q1
Q0
02012 QQQQD  02011 QQQQD  12122 QQQQD 

22. 22
AAIT, Department of
Electrical and Computer
Engineering
Nebyu Yonas Sutri
 Design the three bit gray counter using D
Flip-Flops individually.
 Design an even bit counter in the following
counting sequence (0,2,4,6,8,0)
 Design an odd bit counter in the following
counting sequence (1,3,5,7,9,1)
What to Do this Week?