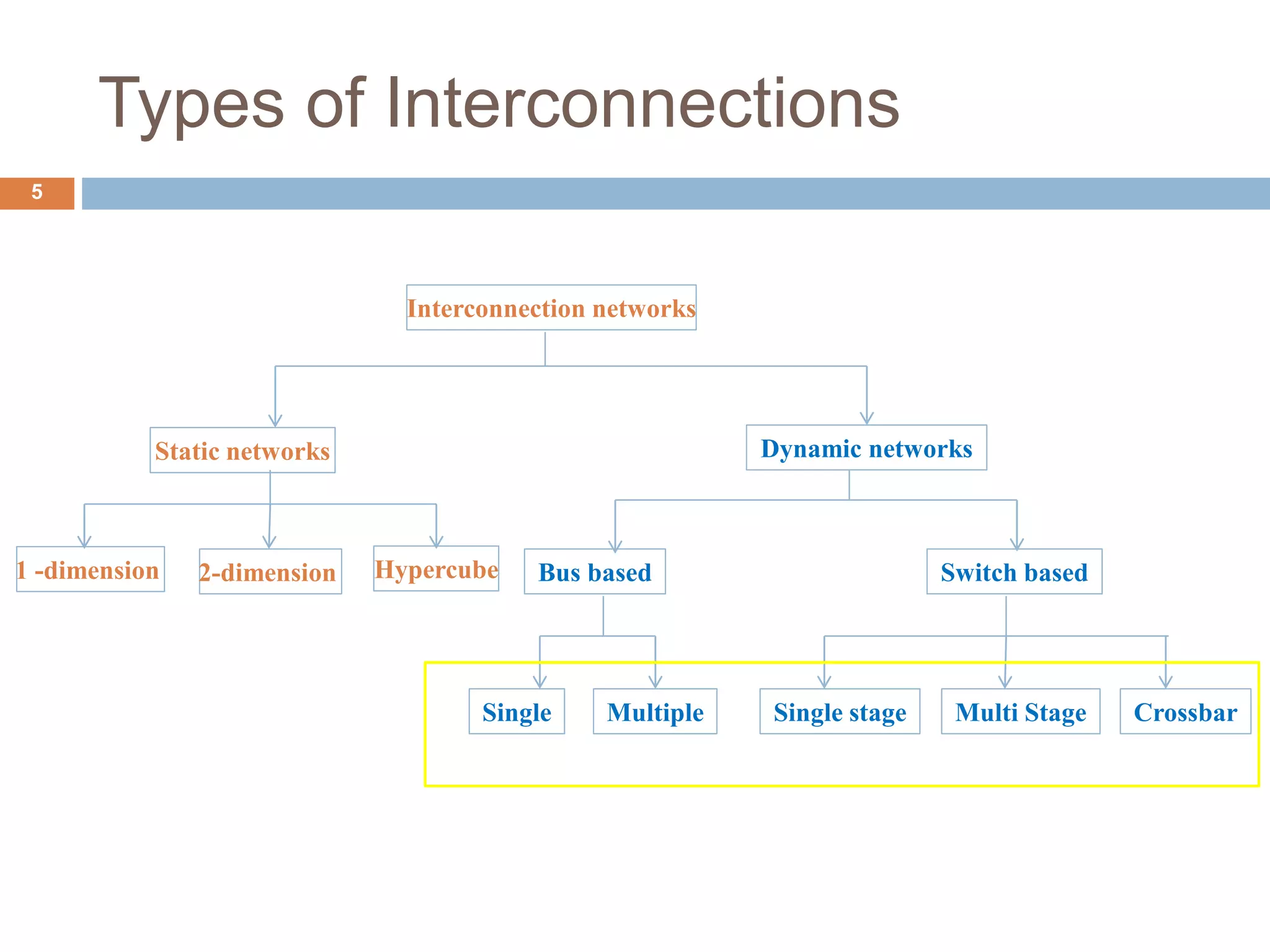
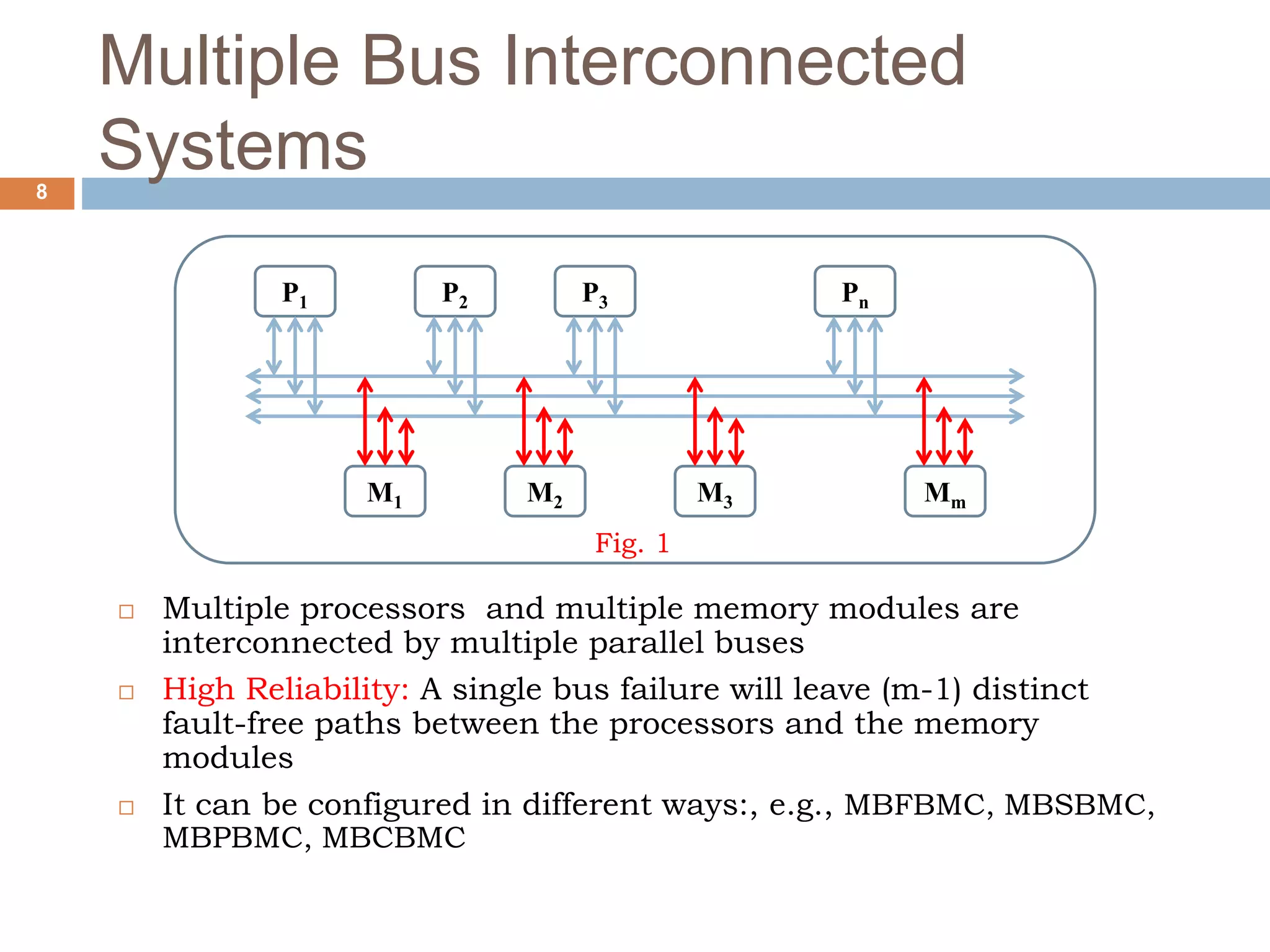
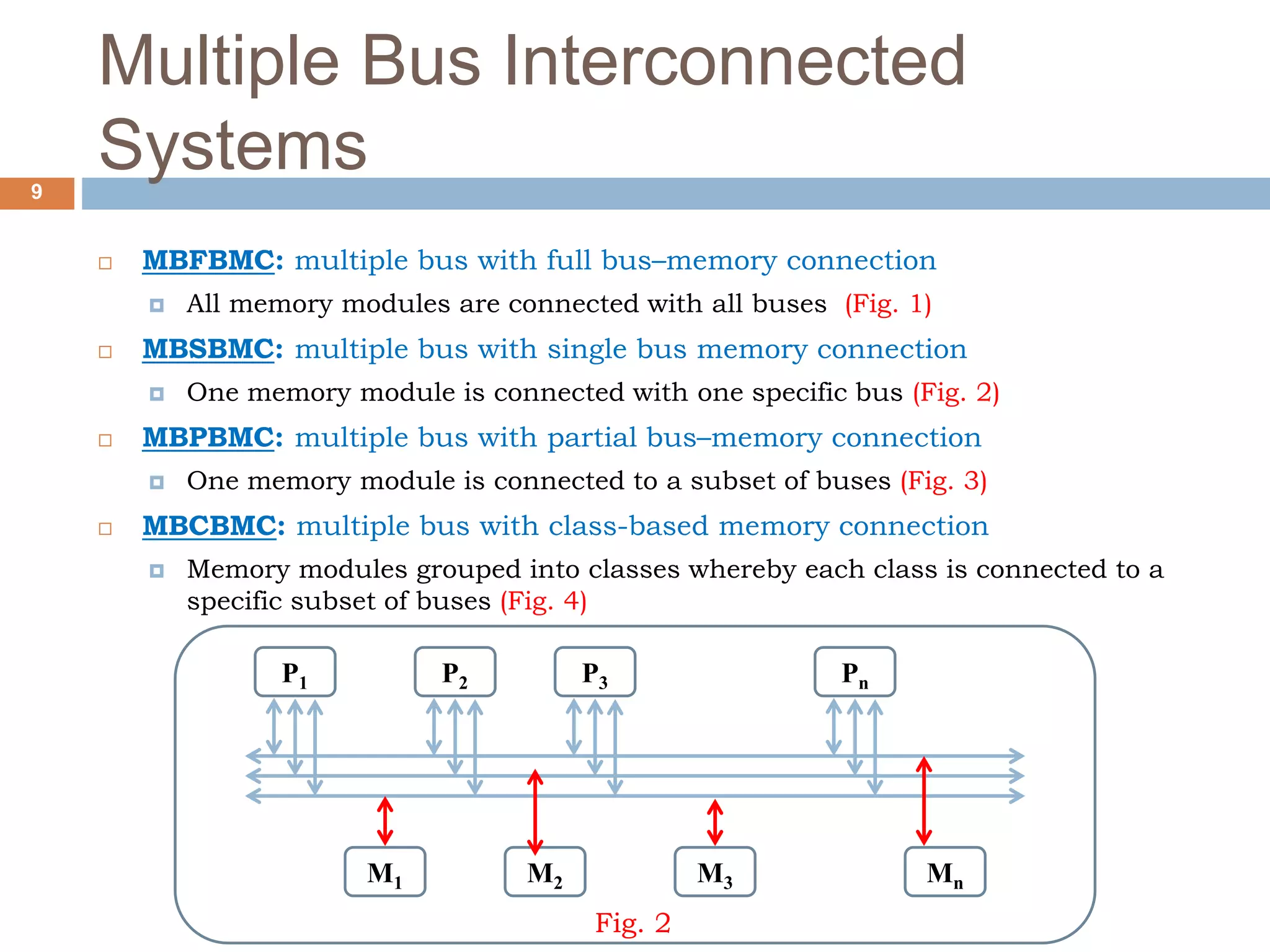
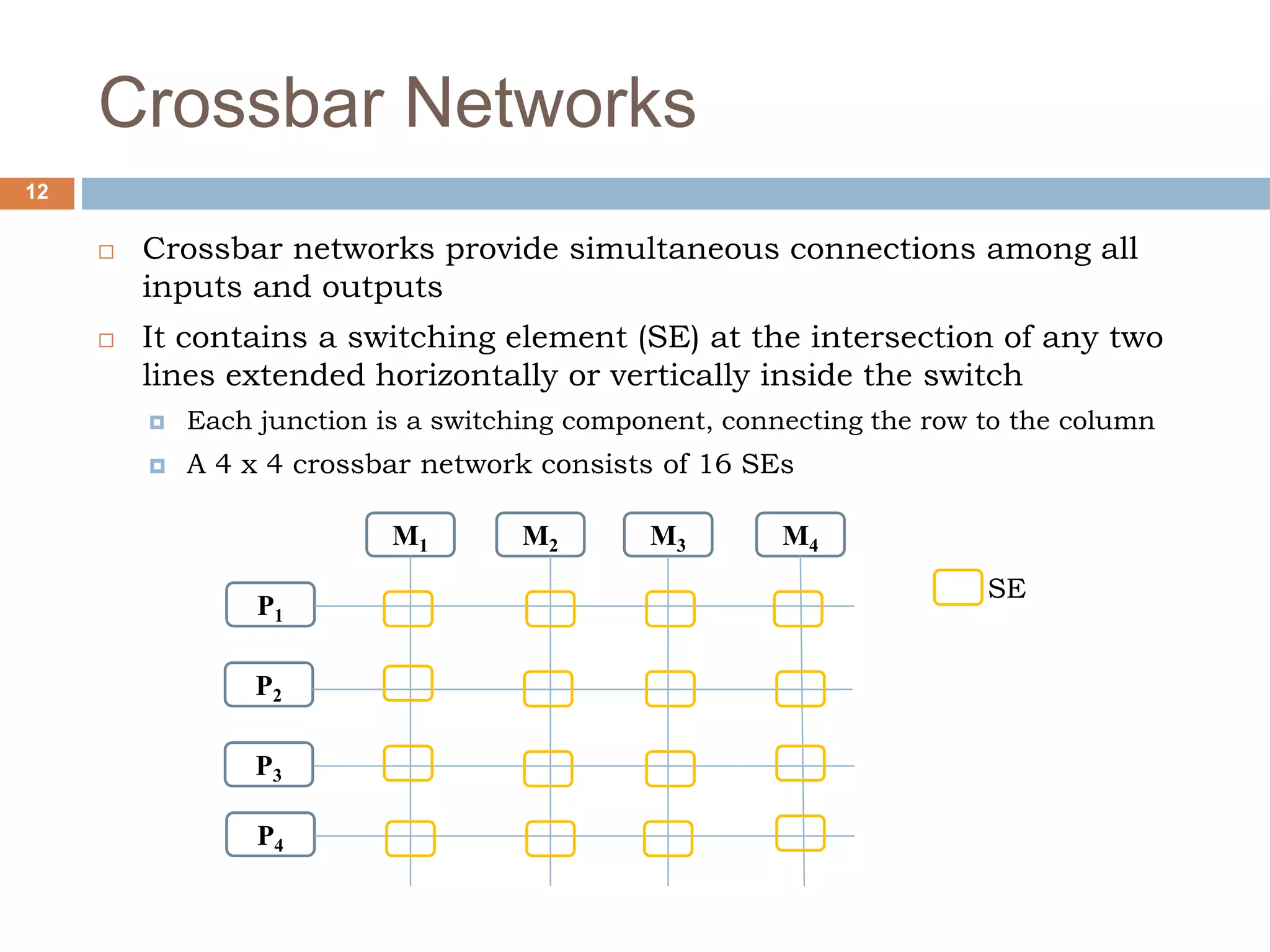
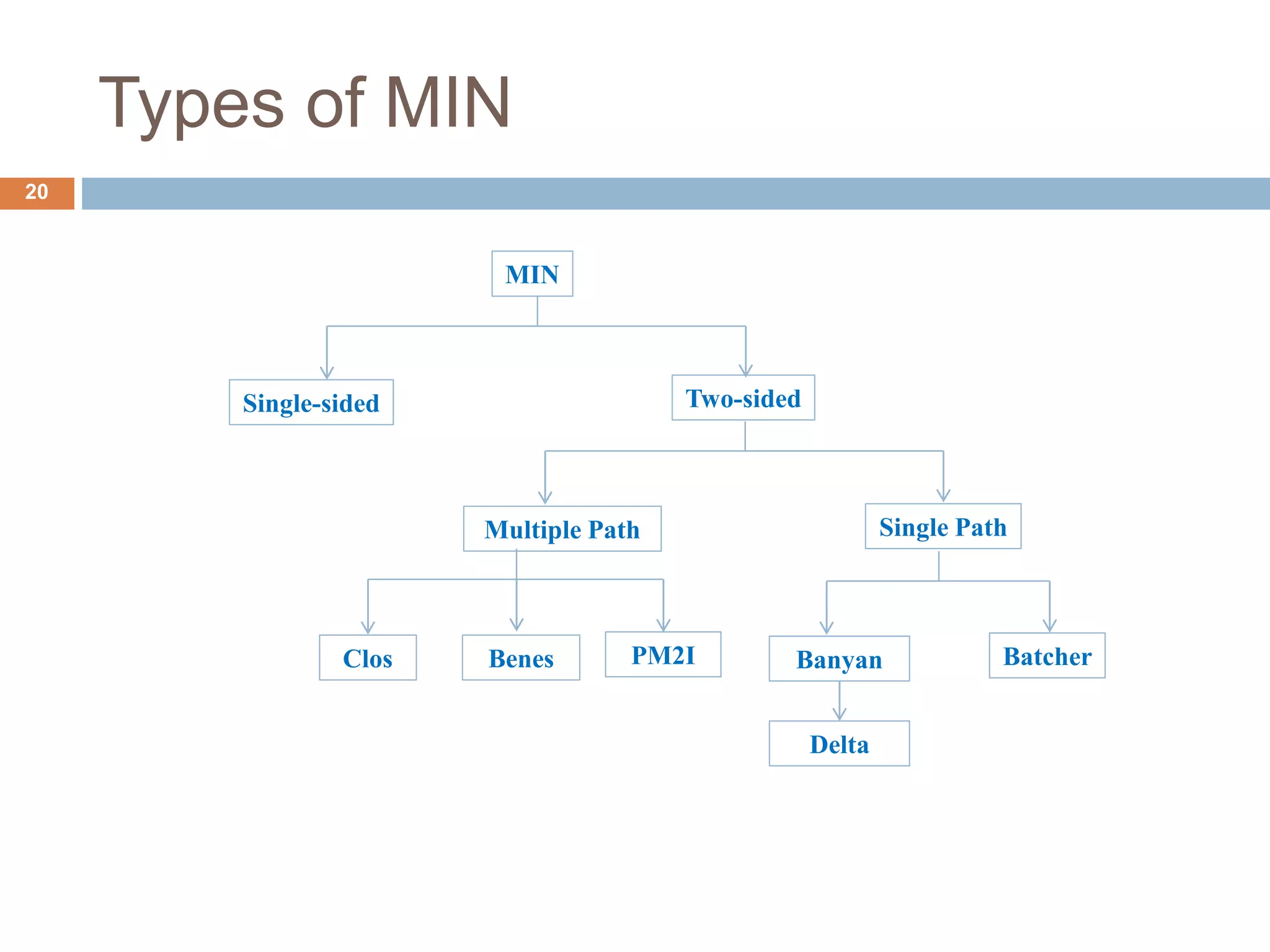
The document discusses dynamic interconnection networks which consist of multiple processors and memory modules connected in various ways, either statically or dynamically. It explains key concepts such as bisection width, types of interconnection networks—like static and dynamic, bus-based, and switch-based networks—and their associated complexities and latencies. Additionally, the document details configurations of bus networks, crossbar networks, single stage interconnection networks, and multistage networks, outlining their operational mechanics and comparative performances.

1. DYNAMIC
INTERCONNECTION
NETWORKS
Dr. Prasenjit Dey

2. Basics
2
 Interconnection networks consists of multiple processors
and memory modules
 The processors and memory modules can be connected
with each other in various ways
 These connections can be static or dynamic
 In static networks, connections are fixed links
 In dynamic network, connections are built on the fly as
required

3. Network properties
3
 Degree of a node (d)
 The number of edges incident on a node
 In-degree
 Out-degree
 In-Degree of a node
 The number of incoming edges of a node
 Out-Degree of a node
 The number of outgoing edges of a node
 Diameter of a node (D)
 The maximum shortest path between any two
nodes
 Network latency
 Worst-case time for a information to be
transferred
d = 5
In-degree = 3
Out-degree = 2
D = max(1,1,2,1,2,1)
= 2
1
2
3
4

4. Bisection of a network
4
 Bisection width
 The minimum number of wires that must be cut to divide the network
into two equal halves.
 A cut of a network C(A, B) is a set of channels, which partition the
set of all nodes into 2 disjoint sets, where each element of C(A, B) is
a channel with a source in A and destination in B or vice versa
 A bisection of a network is a cut that partitions the network into
equal halves, such that |A|≤|B|≤|A+1|
 The channel bisection of a network is the minimum channel count
over all bisections of the network
|
)
,
(
|
min
sec
B
A
C
Bc
tions
bi


5. Types of Interconnections
5
Interconnection networks
Static networks Dynamic networks
2-dimension Bus based
1 -dimension Hypercube Switch based
Single Multiple Single stage Multi Stage Crossbar

6. Bus based Interconnection
Networks
6
 All the processors and memory modules are interconnected
with each other by buses
 Two types of bus based networks
 Single bus networks
 Multiple bus networks

7. Single Bus Interconnected
Systems
7
 Multiple processors are interconnected by a single shared bus
 Each processor has its own cache, less traffic
 All processors communicate with a single shared memory
 Number of buses used is 1, so the network complexity is O(1)
 Maximum input to output delay is n, so time complexity is O(n)
P1 P2 P3 Pn
Shared
Memory
I/O
devices
Shared bus

8. Multiple Bus Interconnected
Systems
8
 Multiple processors and multiple memory modules are
interconnected by multiple parallel buses
 High Reliability: A single bus failure will leave (m-1) distinct
fault-free paths between the processors and the memory
modules
 It can be configured in different ways:, e.g., MBFBMC, MBSBMC,
MBPBMC, MBCBMC
P1 P2 P3 Pn
M1 M2 M3 Mm
Fig. 1

9. Multiple Bus Interconnected
Systems
9
 MBFBMC: multiple bus with full bus–memory connection
 All memory modules are connected with all buses (Fig. 1)
 MBSBMC: multiple bus with single bus memory connection
 One memory module is connected with one specific bus (Fig. 2)
 MBPBMC: multiple bus with partial bus–memory connection
 One memory module is connected to a subset of buses (Fig. 3)
 MBCBMC: multiple bus with class-based memory connection
 Memory modules grouped into classes whereby each class is connected to a
specific subset of buses (Fig. 4)
P1 P2 P3 Pn
M1 M2 M3 Mn
Fig. 2

10. Multiple Bus Interconnected
Systems
P1 P2 P3 Pn
M1 M2 M3 M4
Fig. 4
P1 P2 P3 Pn
M1 M2 M3 M4
Fig. 3
Class 1 Class 2

11. Switch-Based Interconnection
Networks
11
 All the processors and memory modules are interconnected
with each other via switches
 Types of switch based networks
 Crossbar Networks
 Single-Stage Networks
 Multistage Networks

12. Crossbar Networks
12
 Crossbar networks provide simultaneous connections among all
inputs and outputs
 It contains a switching element (SE) at the intersection of any two
lines extended horizontally or vertically inside the switch
 Each junction is a switching component, connecting the row to the column
 A 4 x 4 crossbar network consists of 16 SEs
P1
P2
P3
P4
M1 M2 M3 M4
SE

13. Crossbar Networks
13
 Two types of settings for SE
1. Straight
2. Diagonal
 In an N x N crossbar, the number of switching points is N2,
so the network complexity is O(N2)
 Not scalable
 Maximum input to output delay is 1, so time complexity is O(1)
 Fast Transfer
 Blocking if the destination is in use
Straight switch
Diagonal switch

14. Switches
Switch size Permutation
connection
Legitimate states
2 × 2 2 4
4 × 4 24 256
8 × 8 40,320 16,777,216
N × N N! NN
14
 Permutation connection
 Each input can only be connected to a single output
 Legitimate state
 Each input can be connected to multiple outputs, but
each output can only be connected to a single input

15. Single Stage Networks
15
 In single stage Interconnection Networks (INs), a simple 2 x 2
switching element (SE) is used
 Four types of settings for SE
 Shuffle-Exchange interconnection pattern is used to
establish the connections between inputs and outputs
 For m-bit input address Pm-1, Pm-2, …, P1, P0
 Shuffle operation performs 1bit circular left shift on the bits
 Shuffle(Pm-1, Pm-2, …, P1, P0) = Pm-2, Pm-3, …, P0, Pm-1
 Exchange operation inverts the LSB
 Exchange(Pm-1, Pm-2, …, P1, P0) = Pm-1, Pm-2, …, P1, 𝑃0
*From Advanced Computer Architectures, K. Hwang, 1993.

16. 16
 Single stage Shuffle-Exchange IN
 Perfect shuffle operation
 cyclic shift 1 place left
 000(0)  000(0)
 001(1)  010(2)
 010(2)  100(4)
 011(3)  110(6)
 100(4)  001(1)
 101(5)  011(3)
 110(6)  101(5)
 111(7)  111(7)
 Exchange operation
 Invert least significant bit
 E.g., 101(5)  100(4)
*From Ben Macey at http://www.ee.uwa.edu.au/~maceyb/aca319-2003
Single Stage Networks

17. Demonstration
17
 In an 8-input single stage IN, create a dynamic connection between
input 0 (000) and output (110) by using Shuffle–Exchange
interconnection pattern.
 The following sequence of shuffle/exchange operations is needed
 E(000)  001
 S(001)  010
 E(010)  011
 S(011)  110

18. Single Stage Networks
18
 For N number of inputs(processors) and N number of
outputs (memory modules), the number of SEs is N/2
 The maximum length of a path from an input to an output in
the network, measured by the number of SEs along the path,
is log2 N.
 In single stage IN, the network complexity is O(N)
 In single stage IN, the time complexity is O(N)
 A single path between the inputs (processors) and the
outputs (memory modules)

19. Multistage Networks
19
 Multistage Interconnection Network (MIN) are formed by
cascading multiple single stage IN each with a set of 2 x 2 SEs
 Stages are connected to each other using Inter Stage Connection
(ISC) Pattern
 The patterns can use any routing function
 E.g., Shuffle–Exchange, Butterfly, Cube, etc.
 Two types of MIN
 Single path MIN
 One unique path between any input/output pair
 Banyan network
 Multipath MIN
 Multiple paths between any input/output pair
 Delta network is a subset of Banyan network which shows self-
routing property

20. Types of MIN
20
MIN
Single-sided Two-sided
Multiple Path Single Path
Clos Benes PM2I Banyan Batcher
Delta

21. Multistage Networks
21
 Based on blocking, there are 3 types of MINs
 Nonblocking
 A network is called nonblocking if it is possible to establish a
connection between an input and an output regardless of what
other connections are currently in process
 Rearrangeable nonblocking
 A network is called rearrangeable nonblocking if it is possible to
establish all possible connections between inputs and outputs by
rearranging its existing connections
 Blocking interconnection
 A network is called blocking if some connections between inputs
and outputs block other input-output connections
 E.g., Omega network, Baseline network, Banyan network, etc.

22. Single Path: Omega network
22
Connect input (processor) 101 to output (memory module) 001
*From Ben Macey at http://www.ee.uwa.edu.au/~maceyb/aca319-2003
Algorithm
At stage k, look at the kth bit of the
destination address
If (kth bit == 0)
consider upper o/p port of the switch
Else
consider lower o/p port of the switch
Input = 101(5)
Shuffle(101) 011(3)
Consider upper port of switch B #1st bit of the
destination address at stage 1 is 0
Shuffle(010) 100(4)
Consider upper port of switch G #2nd bit of the
destination address at stage 2 is 0
Shuffle(100) 001(1)
Consider lower port of switch I #3rd bit of
the destination address at stage 3 is 1

23.  Suppose there is a connection from input 001 to output 100
 Try to establish a connection between input 011 and output 101
 It will make a collision at the upper output of 4th switch in 2nd
stage, therefore blocking the connection between input 011 and
output 101
Blocking in Omega network

24. Omega networks
24
 Uses 2 × 2 switches and perfect shuffle interconnect
pattern between the stages
 One unique path from each input to each output, no
redundant paths
 no fault tolerance and the possibility of blocking
 For N number of inputs and N number of outputs
 Number of stages is log2N (for 2 × 2 switches)
 Number of SEs per stage is N/2
 Total number of SEs is (N/2) log2(N)
 Number of permutations in a omega network is 2(N/2) log2(N)

25. Baseline networks
25
 This is another type of blocking network that can be generated
recursively
 The 1st stage N × N, the second (N/2) × (N/2), and so on
 Networks are topologically equivalent
 A network can be reproduced from the other networks by rearranging the
nodes at each stage.
*From Advanced Computer Architectures, K. Hwang, 1993.

26.  It is an 8 x 8 Benes network
 Here, the connection 110-100 blocks the connection between
input 100 and output 010
 However, by rearranging the 110-100 connection, it is possible
to establish a connection between input 100 and output 010
001
010
011
100
101
000
110
111
001
010
011
100
101
000
110
111
001
010
011
100
101
000
110
111
001
010
011
100
101
000
110
111
Multiple Path: Benes network

27. Performance Comparison
27
 Bus network
 Blocking
 Network complexity O(1)
 Network latency O(N)
 Crossbar network
 Non blocking
 Network complexity O(N2)
 Network latency O(1)
 Single stage IN
 Blocking
 Network complexity O(N)
 Network latency O(N)
 Multistage IN
 Blocking
 Network complexity O(N log2 N)
 Network latency O(log2 N)

28. 28
Thank You