This document discusses strongly connected components (SCCs) in directed graphs. It defines an SCC as a maximal set of vertices where each vertex is mutually reachable from every other. The algorithm works by running DFS on the original graph and its transpose to find SCCs, processing vertices in decreasing finishing time order from the first DFS. Vertices belonging to the same DFS tree in the second graph traversal are in the same SCC.

1. Strongly Connected Components
Prepared by
Md. Shafiuzzaman
Lecturer, Dept. of CSE, JUST

2. Md. Shafiuzzaman 2
Strongly Connected Components
 A directed graph is strongly connected if there is a path between
all pairs of vertices.
 A strongly connected component (SCC) of a directed graph is a
maximal strongly connected subgraph.

3. Md. Shafiuzzaman 3
Strongly Connected Components
a strongly connected component (SCC) of a directed graph
G(V,E) is a maximal set of vertices U V such that
– For each u,v U we have both u  v and v  u
i.e., u and v are mutually reachable from each other (u  v)
Let GT(V,ET) be the transpose of G(V,E) where
ET {(u,v): (u,v)  E}
– i.e., ET consists of edges of G with their directions reversed
Constructing GT from G takes O(V+E) time (adjacency list rep)
Note: G and GT have the same SCCs (u  v in G u  v in GT)

4. Md. Shafiuzzaman 4
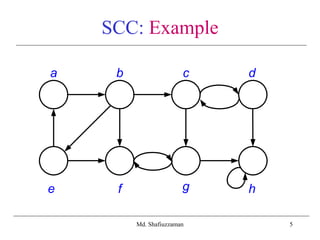
Strongly Connected Components
Algorithm
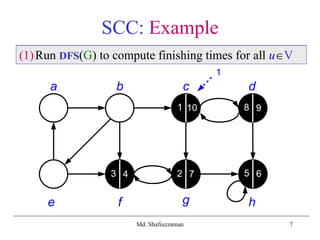
(1) Run DFS(G) to compute finishing times for all uV
(2) Compute GT
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] computed in Step (1)
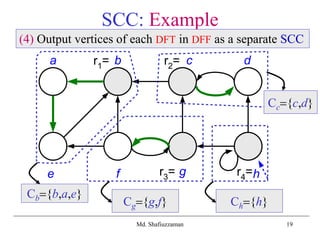
(4) Output vertices of each DFT in DFF of Step (3) as a
separate SCC

5. Md. Shafiuzzaman 5
SCC: Example
a b c
e
d
f g h

6. Md. Shafiuzzaman 6
SCC: Example
a b c
e
d
f g h
1
1
(1)Run DFS(G) to compute finishing times for all uV

7. Md. Shafiuzzaman 7
SCC: Example
a b c
e
d
f g h
1
1
10
2 73 4 5 6
8 9
(1)Run DFS(G) to compute finishing times for all uV

8. Md. Shafiuzzaman 8
SCC: Example
a b c
e
d
f g h
1
2
10
2 73 4 5 6
8 911
(1)Run DFS(G) to compute finishing times for all uV

9. Md. Shafiuzzaman 9
SCC: Example
a b c
e
d
f g h
1
2
10
2 73 4 5 6
8 916111413
1512
1
Vertices sorted according to the finishing times:
b, e, a, c, d, g, h, f 

10. Md. Shafiuzzaman 10
SCC: Example
a b c
e
d
f g h
(2)Compute GT

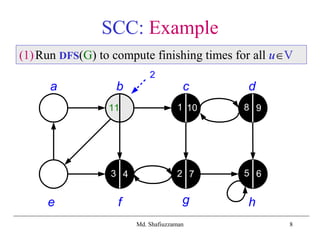
11. Md. Shafiuzzaman 11
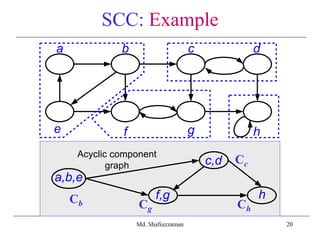
SCC: Example
a b c
e
d
f g h
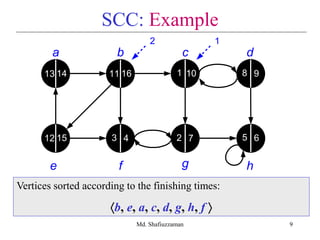
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] order: b, e, a, c, d, g, h, f 

12. Md. Shafiuzzaman 12
SCC: Example
a b c
e
d
f g h
r1=
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] order: b, e, a, c, d, g, h, f 

13. Md. Shafiuzzaman 13
SCC: Example
a b c
e
d
f g h
r1=
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] order: b, e, a, c, d, g, h, f 

14. Md. Shafiuzzaman 14
SCC: Example
a b c
e
d
f g h
r1= r2=
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] order: b, e, a, c, d, g, h, f 

15. Md. Shafiuzzaman 15
SCC: Example
a b c
e
d
f g h
r1= r2=
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] order: b, e, a, c, d, g, h, f 

16. Md. Shafiuzzaman 16
SCC: Example
a b c
e
d
f g h
r1= r2=
r3=
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] order: b, e, a, c, d, g, h, f 

17. Md. Shafiuzzaman 17
SCC: Example
a b c
e
d
f g h
r1= r2=
r3=
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] order: b, e, a, c, d, g, h, f 

18. Md. Shafiuzzaman 18
SCC: Example
a b c
e
d
f g h
r1= r2=
r3= r4=
(3) Call DFS(GT) processing vertices in main loop in
decreasing f[u] order: b, e, a, c, d, g, h, f 

19. Md. Shafiuzzaman 19
SCC: Example
a b c
e
d
f g h
r1= r2=
r3= r4=
(4) Output vertices of each DFT in DFF as a separate SCC
Cb{b,a,e}
Cg{g,f} Ch{h}
Cc{c,d}

20. Md. Shafiuzzaman 20
SCC: Example
a b c
e
d
f g h
hf,g
c,d
a,b,e
Acyclic component
graph
Cb Cg
Cc
Ch