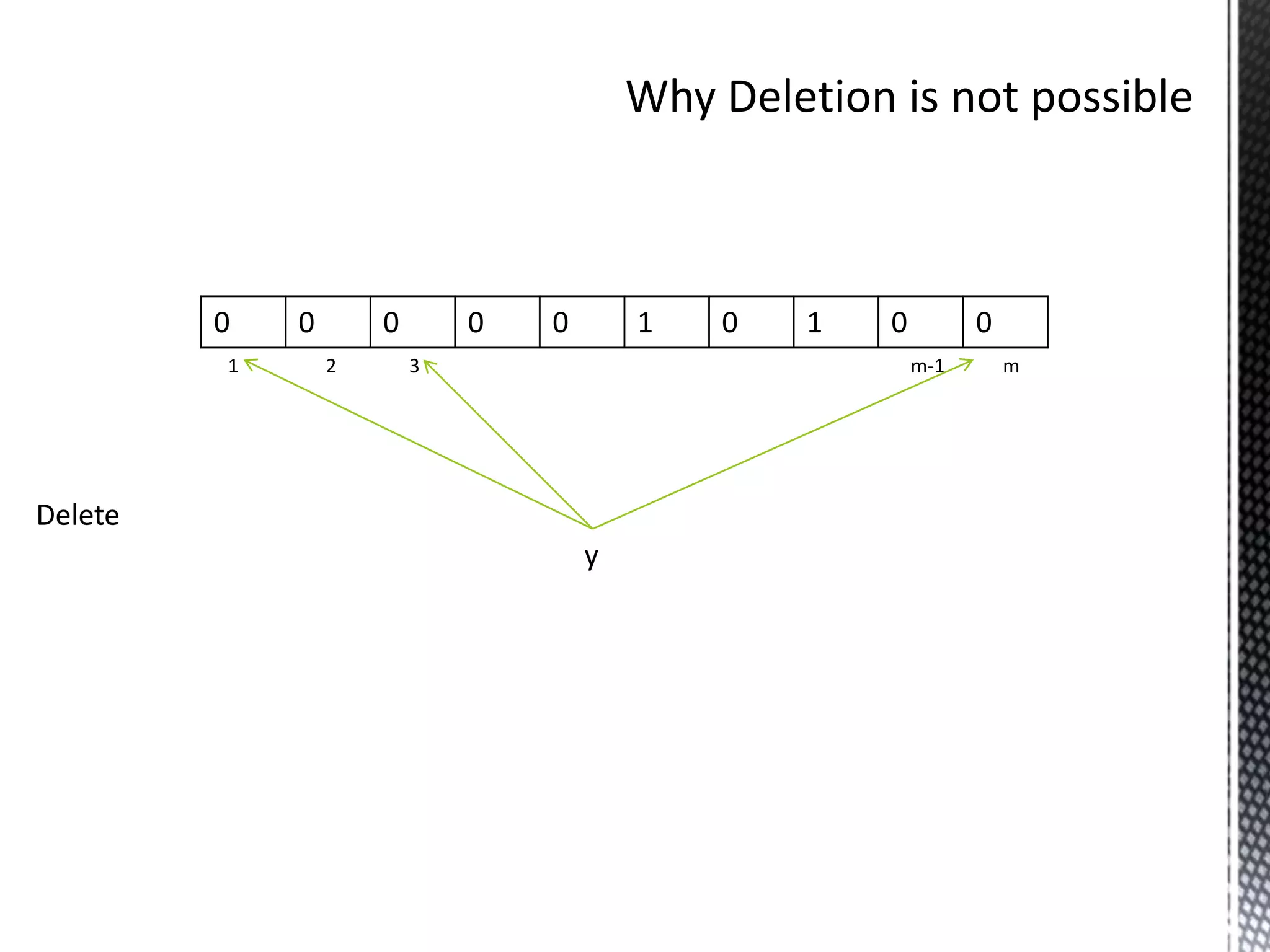
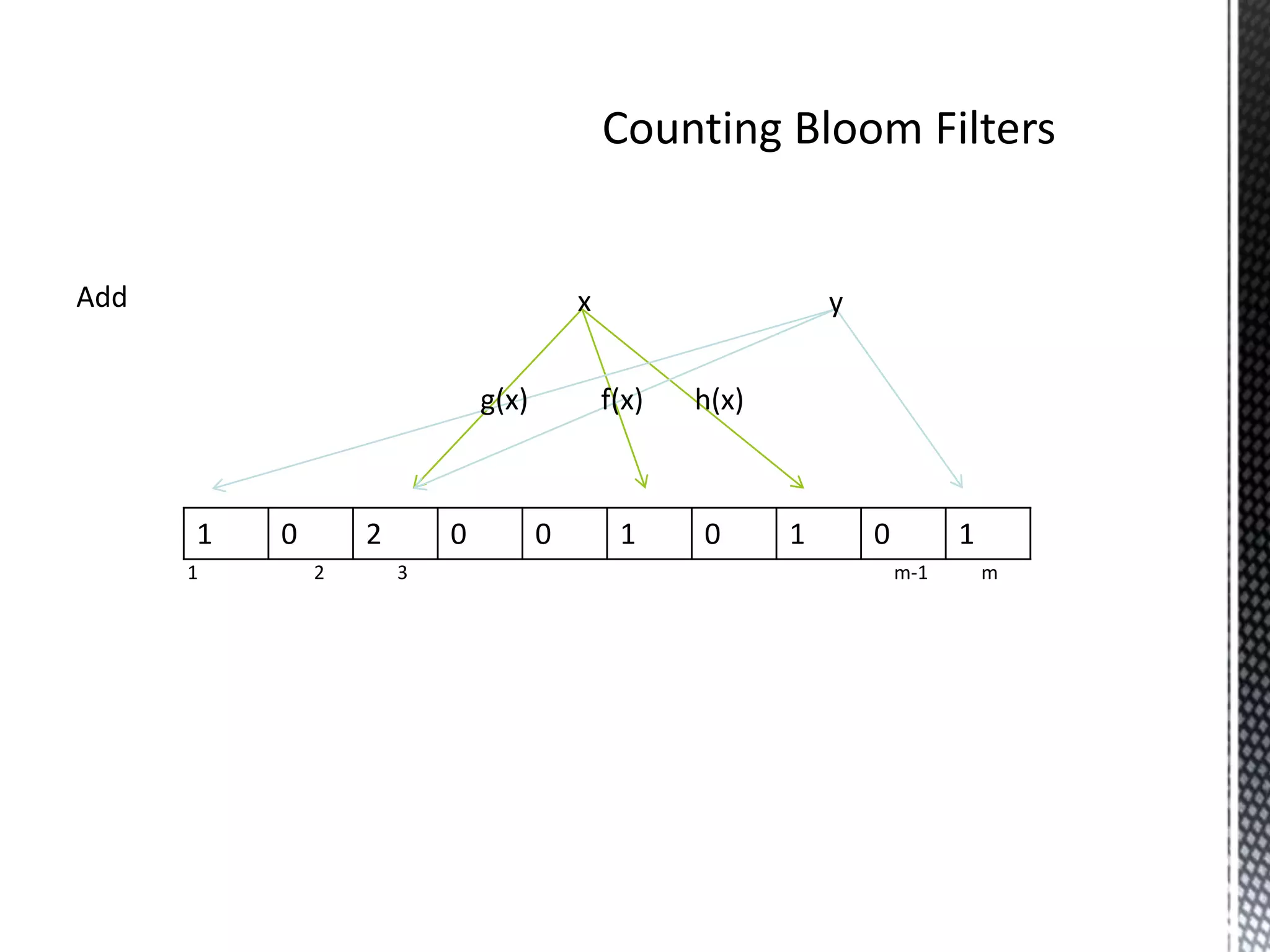
The document discusses Bloom filters, which are compact data structures used to represent sets probabilistically. Bloom filters allow membership queries to determine if an element is in a set, but may return false positives. They provide a more space-efficient alternative to other data structures like hash tables. The key properties of Bloom filters are that they require less memory than other solutions, allow fast membership checking, and never return false negatives, though they can return false positives. Several applications of Bloom filters are also mentioned such as spell checkers, password checking, and caching.

2. That data structure should enable two operations:
 the ability to add an extra object ‘x’ to the set
‘S’; and
 a test to determine whether a given object ’x’ is
a member of ‘S’.
Motivation is that this operation should be
perform keeping in mind space and time factor.

3.  In these approach we use single Hash Function.
 A Hash Function is any algorithm that maps large data sets of
variable length to smaller data sets of fixed length.
 They are used to accelerate table lookup or finding element in
sets.

4. • The problem with hashed based approach is that
they have high false positive element probability:
• Other is that hash based approach required more
memory space.
• Also the query cost incurred is really very high.
So some new less memory and space consuming
solution was required to reduce cost.

5. Bloom filters are compact data structures for
probabilistic representation of a set in order to
support membership queries (i.e. queries that
ask: “Is element X in set Y?”). This compact
representation is the payoff for allowing a small
rate of false positives in membership queries; that
is, queries might incorrectly recognize an element
as member of the set.

6.  Bloom filters have a strong space advantage over other data
structures for representing sets, such as self-balancing binary
search trees, hash tables, or simple arrays or linked lists of
the entries.
 It does not store the object itself.

7.  It was developed by Burton Howard Bloom in 1970.
 Bloom filters are called filters because they are often used as
a cheap first pass to filter out segments of a dataset that do
not match a query.

8. m bits array(initially set to 0)
K hash functions
-consider hash function as g(x),f(x),h(x).
0 0 0 0 0 0 0 0 0 0
0 1 2 m-1 m

9. Insert(Table,Key)
1. i=0
2. Repeat
3. i=i+1
m bits array(initially set to 0) 4. pass key -> hash funct & set index 1
5. Until((i==k))
K hash functions end
Add x
g(x) f(x) h(x)
0 0 1 0 0 1 0 1 0 0
0 1 2 m-1 m

10. Insert(Table,Key)
1. i=0
2. Repeat
3. i=i+1
m bits array(initially set to 0) 4. pass key -> hash funct & set index 1
5. Until((i==k))
K hash functions end
Add x y
g(x) f(x) h(x)
1 0 1 0 0 1 0 1 0 1
0 1 2 m-1 m

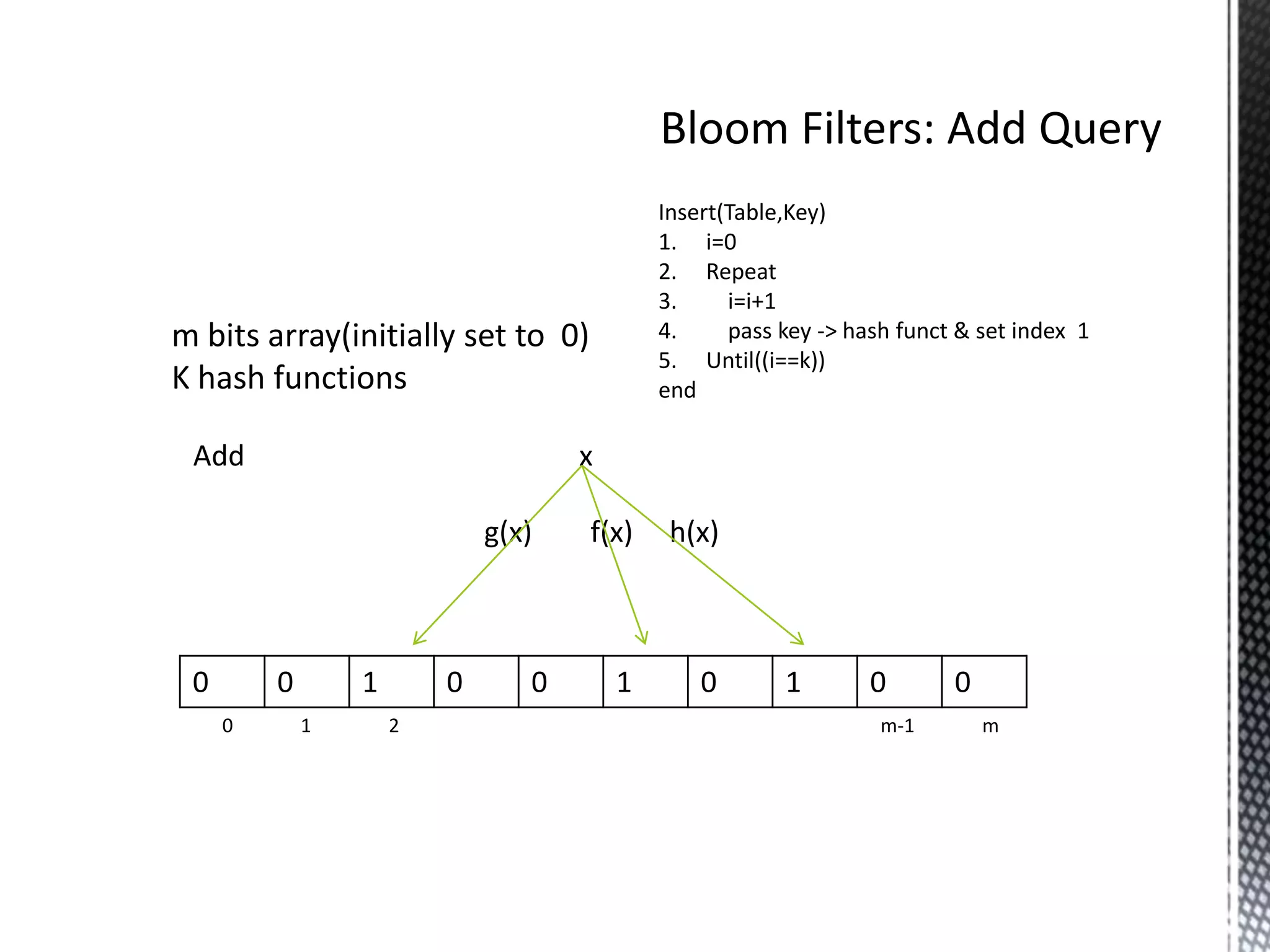
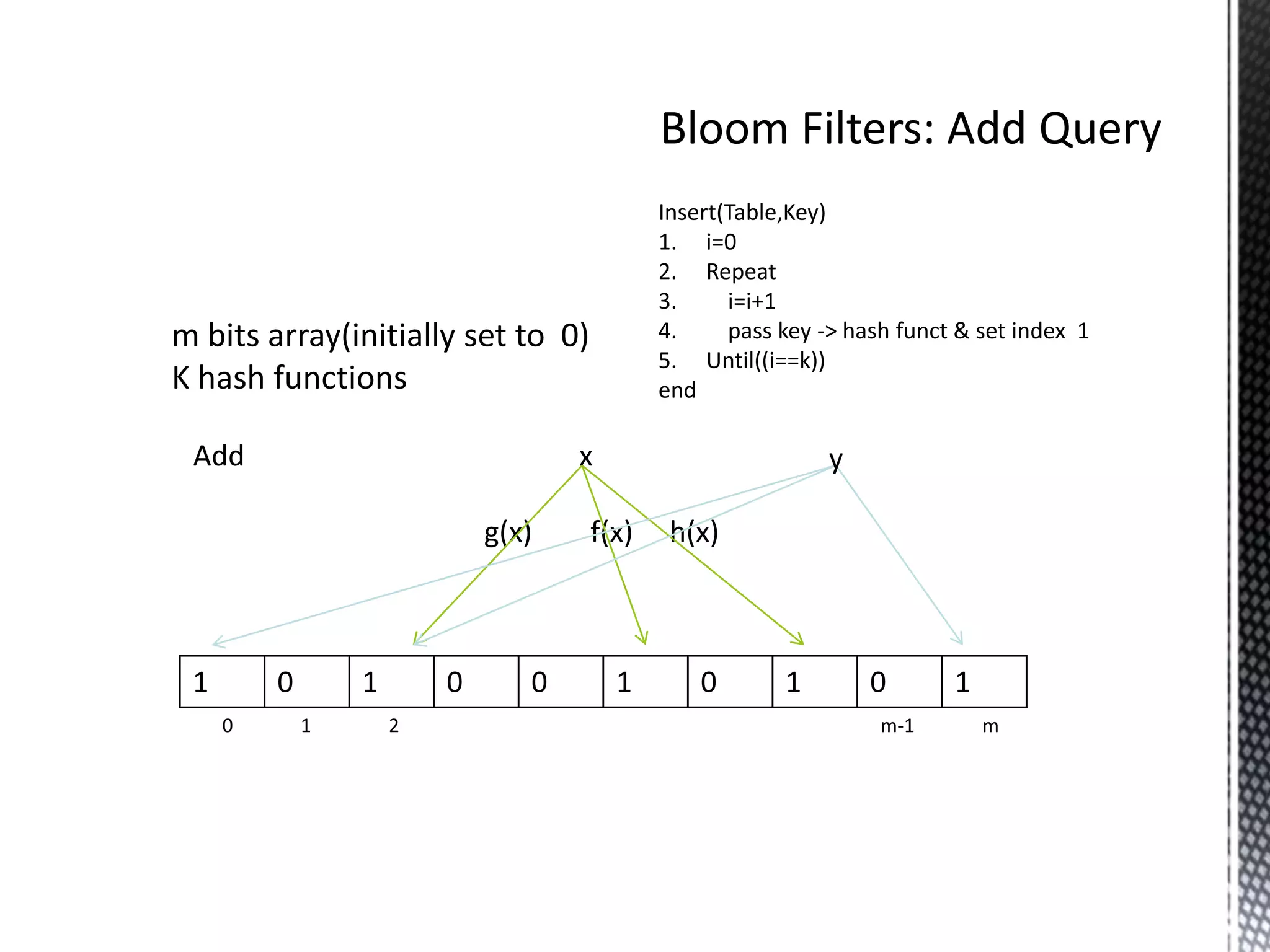
11. IsMember(Table,Key)
1. i=0
2. Repeat
3. i=i+1
m bits array(initially set to 0) 4. hi is the ith hash funct
K hash functions 5. until((i=k) Or(IsSet(Table[hi(key)])))
6. if(i=k) then
7. return true
8. Else
9. return false
end
1 0 1 0 0 1 0 1 0 1
0 1 2 m-1 m
Search y
It return true as y is there in set S

12. 1 0 1 0 0 1 0 1 0 1
0 1 2 m-1 m
Search z

13.  Time needed either to add items or to check whether an item
is in the set is a fixed constant, O(k).
 The false positive probability has decreased to :
 Space used by bloom filters is :

14. Bloom Filters have some attractive properties like
 low storage requirement,
 fast membership checking,
 no false negatives,
 Low false positive probability and
 No deletion is allowed

15. 1 0 1 0 0 1 0 1 0 1
1 2 3 m-1 m
Delete
y

16. 0 0 0 0 0 1 0 1 0 0
1 2 3 m-1 m
Delete
y

17. 1. Compressed Bloom Filter
Using a larger but sparser Bloom Filter can yield the same false
positive rate with a smaller number of transmitted bits.
2. Scalable Bloom Filter
A Scalable Bloom Filters consist of two or more Standard Bloom
Filters, allowing arbitrary growth of the set being represented.
3. Generalized Bloom Filter
Generalized Bloom Filter uses hash functions that can set as well as
reset bits.
4. Stable Bloom Filter
This variant of Bloom Filter is particularly useful in data streaming
applications.
5. Counting Bloom Filter

18. Add x y
g(x) f(x) h(x)
1 0 2 0 0 1 0 1 0 1
1 2 3 m-1 m

19. The application where space is most important uses bloom
filters.
Some Application Of Bloom Filters are:
1. Spell Checker
2. Forbidden Password
3. Chrome uses Bloom Filters
4. ICP(Internet Cache Protocol) Request Handling

20. Proxy
Proxy
Cache
Cache
Client
Proxy
Cache Internet
Proxy
Cache

21. Proxy
Proxy
Cache
Cache
Client
Proxy Proxy Internet
Cache Cache

22.  WikiPedia
 http://www.michaelnielsen.org/ddi/why-bloom-filters-work-the-way-they-do/
 Burton H. Bloom, Space/time trade-offs in Hash Coding with Allowable Errors,.
 BLOOM FILTERS & THEIR APPLICATIONS