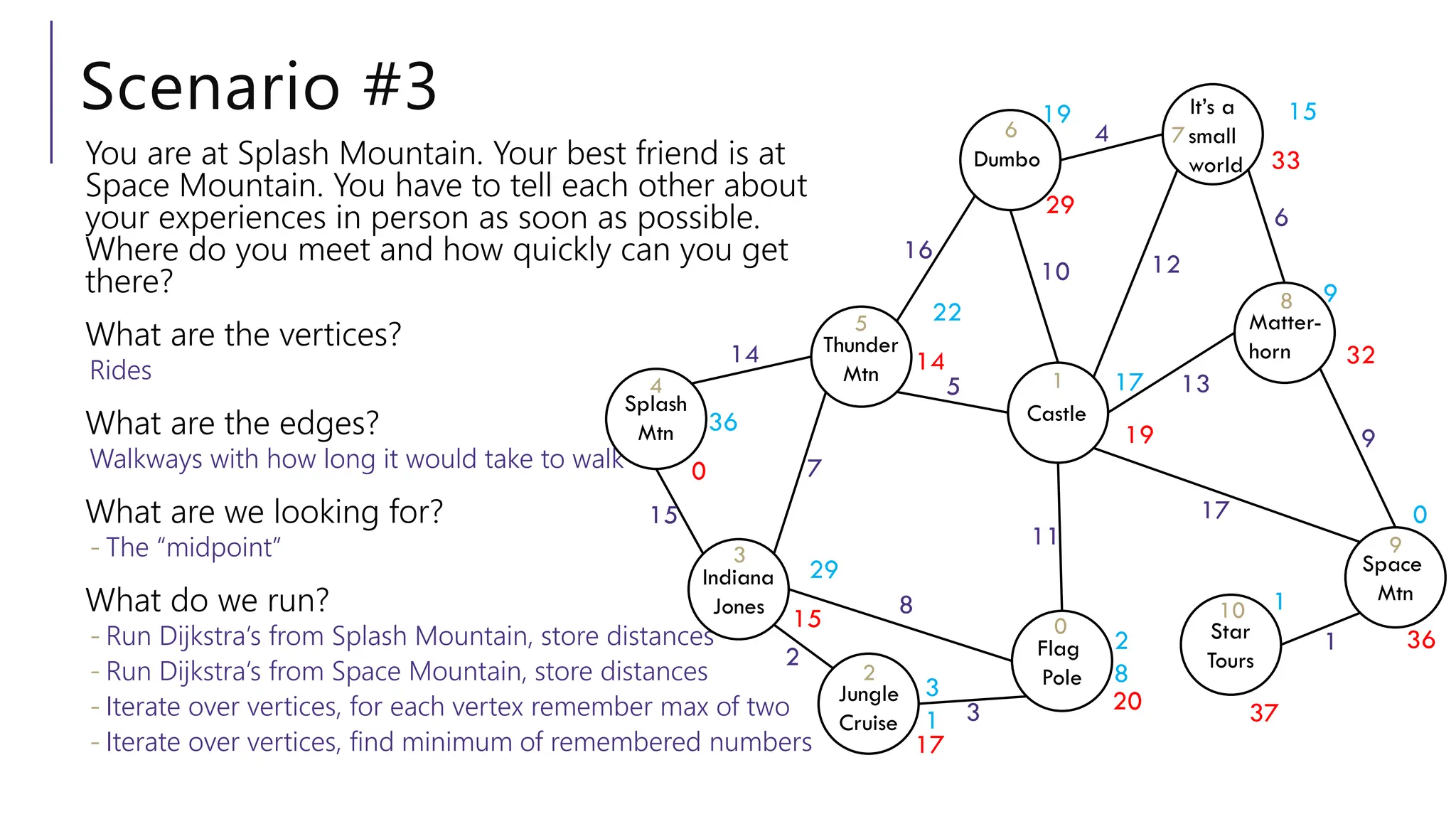
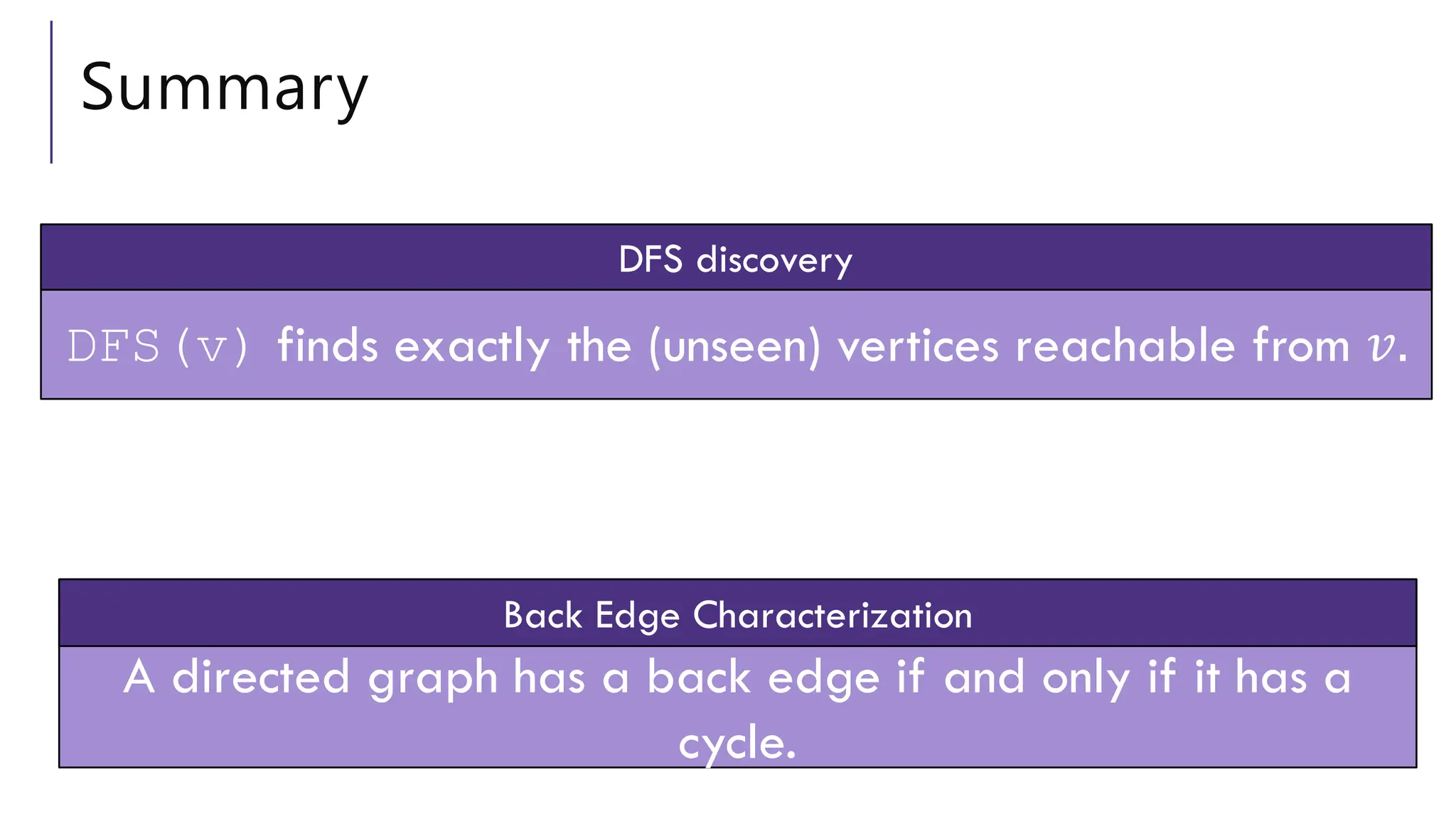
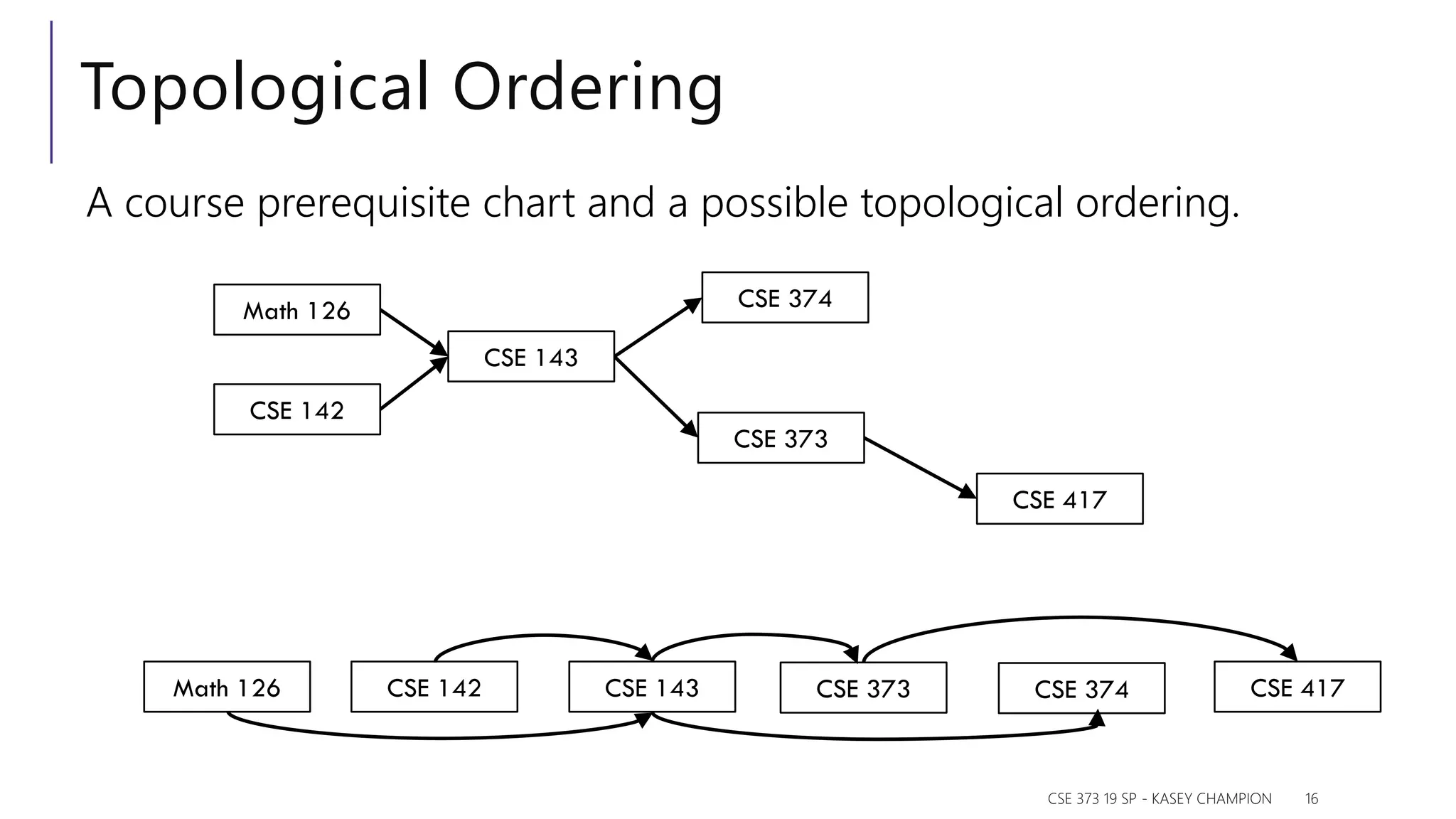
La clase se centra en la búsqueda en grafos utilizando DFS en gráficos dirigidos, definiendo tipos de bordes como bordes de árbol, bordes de retroceso y bordes cruzados, y su relación con la detección de ciclos. Se discuten aplicaciones como la detección de componentes fuertemente conectados y el ordenamiento topológico, junto con ejemplos prácticos para modelar problemas del mundo real en grafos. El proceso de modelado de grafos se detalla, desde la identificación de objetos fundamentales hasta la elección del algoritmo adecuado para resolver el problema.
















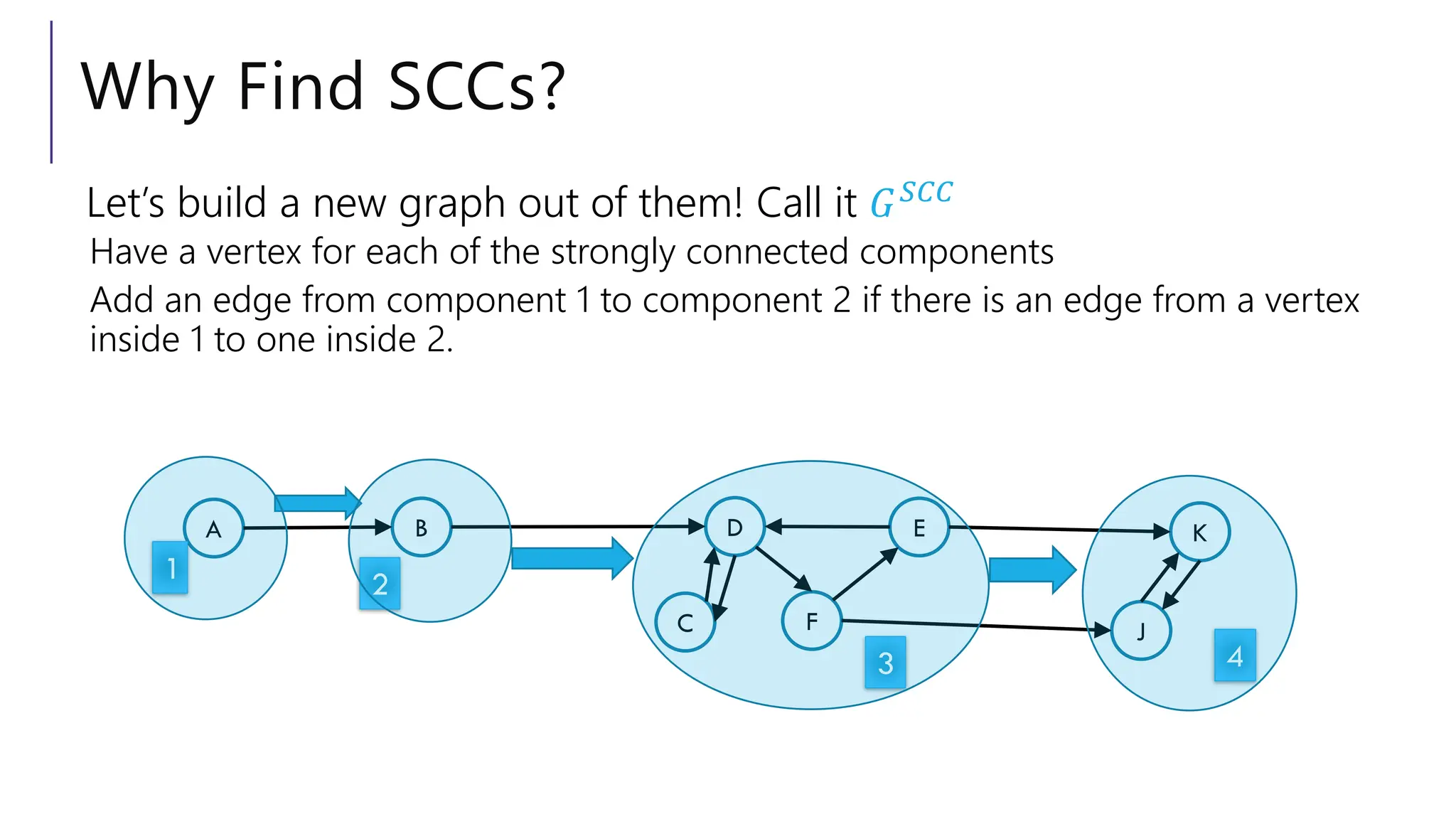
![Designing New Graph Algorithms
Not a common task – most graph problems have been asked before.
When you need to do it, Robbie recommends:
Start with a simpler case (topo-sorted DAG, or [strongly] connected graph).
One of the problems on HW2 does this – it walks you through the process of
designing an algorithm by:
1. Figuring out what you’d do if the graph is strongly connected
2. Figuring out what you’d do if the graph is a topologically ordered DAG
3. Stitching together those two ideas (using 𝐺𝑆𝐶𝐶).](https://image.slidesharecdn.com/06-dfs-model-250114194057-dc269ae3/75/DFS-model-Graph-Modeling-CES-417-Lecture-6-20-2048.jpg)