1) Regular languages have closure properties where certain operations on regular languages produce new regular languages. These include operations like union, concatenation, and Kleene star. 2) Finite automata have several decidable properties including emptiness, non-emptiness, finiteness, infiniteness, membership, and equality. These properties can be checked through operations on the automata like removing unreachable states. 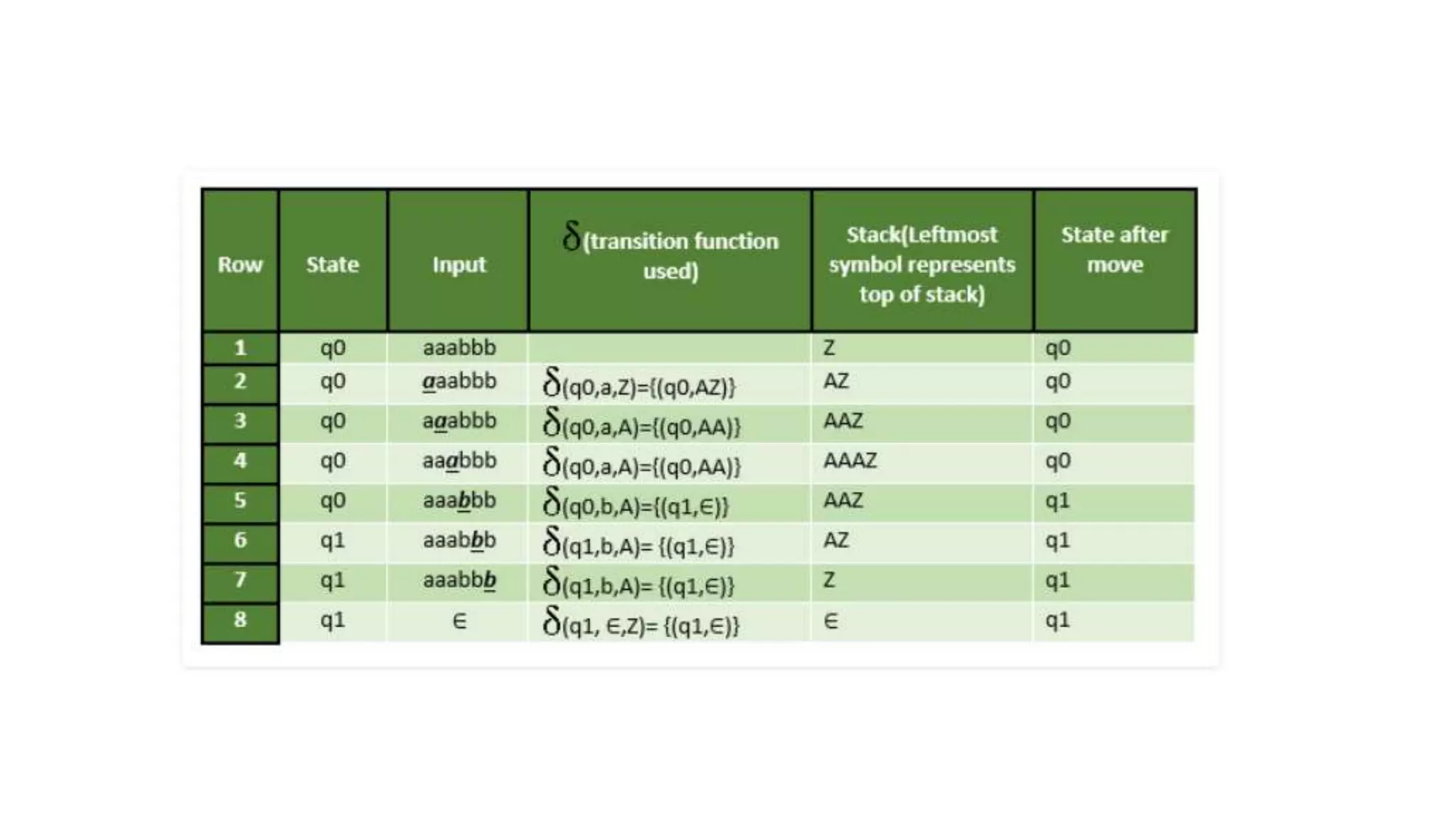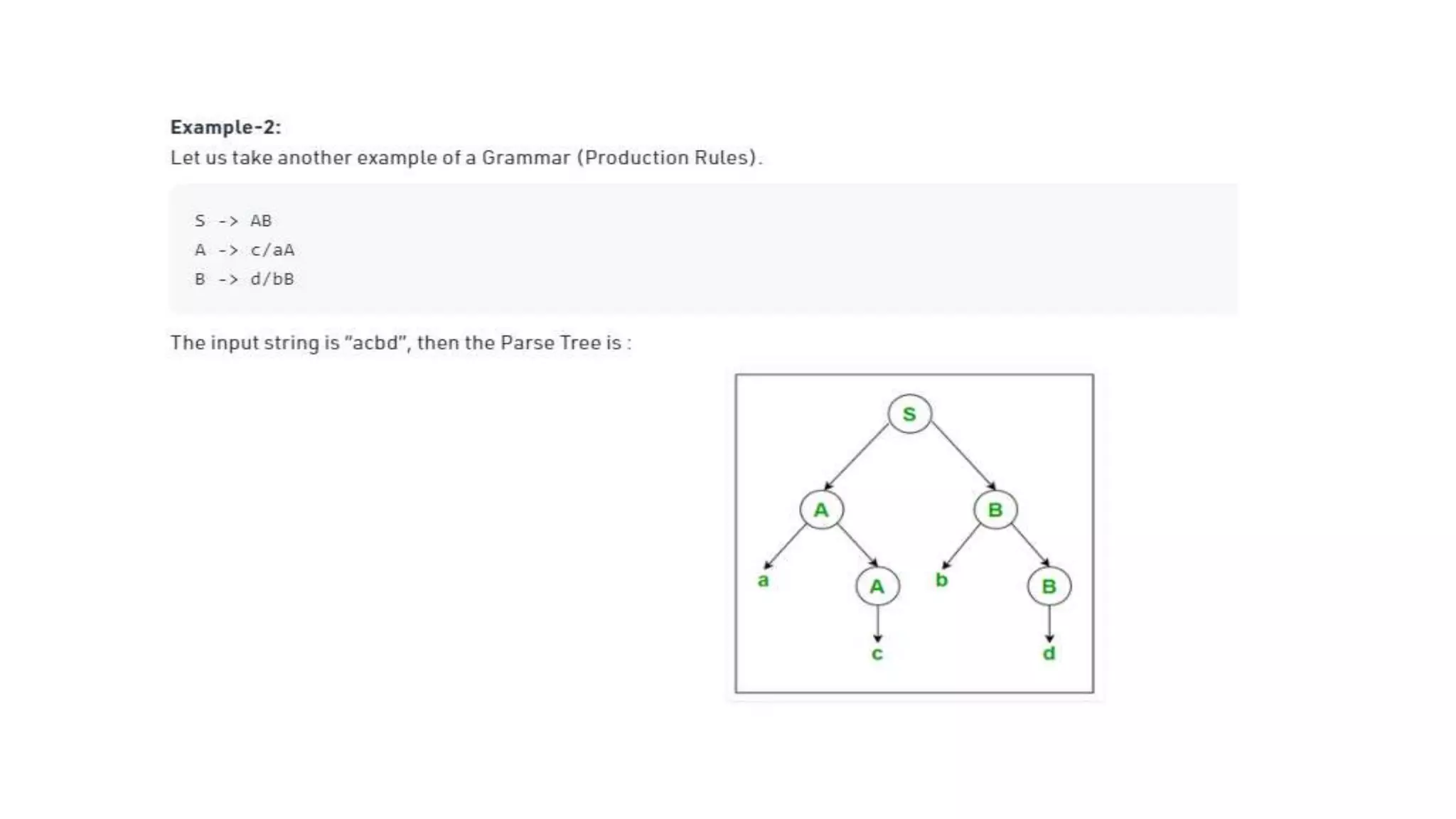3) Pushdown automata extend finite automata with a stack. They can be defined by their states, input symbols, stack symbols, transitions, and acceptance conditions like empty stack. Parse trees provide a hierarchical representation of how the symbols in a string derive from a grammar's starting symbol.

1. 1)CLOSURE PROPERTIES OF
REGULAR LANGUAGE

2. CLOSURE PROPERTIES OF REGULAR
LANGUAGE
closure properties on regular languages are
defined as certain operations on regular language
which are guaranteed to produce regular language.
Closure refers to some operation on a language,
resulting in a new language that is of same “type” as
originally operated on i.e., regular.

7. DECISION PROPERTIES
Approximately all the properties are decidable in case of finite
automaton
.
(i)Emptiness
(ii) Non-emptiness
(iii) Finiteness
(iv) Infiniteness
(v) Membership
(vi) Equality

8. EMPTINESS AND NON-EMPTINESS:
•Step-1: select the state that cannot be reached from the initial states
& delete them (remove unreachable states).
•Step 2: if the resulting machine contains at least one final states, so
then the finite automata accepts the non-empty language.
•Step 3: if the resulting machine is free from final state, then finite
automata accepts empty languag

9. FINITENESS AND INFINITENESS:
•Step-1: select the state that cannot be reached from the initial state & delete them
(remove unreachable states).
•Step-2: select the state from which we cannot reach the final state & delete them
(remove dead states).
•Step-3: if the resulting machine contains loops or cycles then the finite automata
accepts infinite language.
•Step-4: if the resulting machine do not contain loops or cycles then the finite
automata accepts infinite language.

10. MEMBERSHIP:
Membership is a property to verify an arbitrary string is accepted by a
finite automaton or not i.e. it is a member of the language or not.
Let M is a finite automata that accepts some strings over an alphabet,
and let ‘w’ be any string defined over the alphabet, if there exist a
transition path in M, which starts at initial state & ends in anyone of the
final state, then string ‘w’ is a member of M, otherwise ‘w’ is not a
member of M.

11. EQUALITY:
Two finite state automata M1 & M2 is said to be
equal if and only if, they accept the same language.
Minimise the finite state automata and the minimal
DFA will be unique.

12. 2)PUSHDOWN AUTOMATA

13. IT CAN BE DEFINED AS:
•Q is the set of states
•∑is the set of input symbols
•Γ is the set of pushdown symbols (which can be pushed and popped from
stack)
•q0 is the initial state
•Z is the initial pushdown symbol (which is initially present in stack)
•F is the set of final states
•δ is a transition function which maps Q x {Σ ∪ ∈} x Γ into Q x Γ*. In a given
state, PDA will read input symbol and stack symbol (top of the stack) and
move to a new state and change the symbol of stack.

14. INSTANTNEOUS DESCRIPTION(ID)
Instantaneous Description (ID) is an informal notation of
how a PDA “computes” a input string and make a decision
that string is accepted or rejected.
A ID is a triple (q, w, α), where:
1. q is the current state.
2. w is the remaining input.
3.α is the stack contents, top at the left.

15. TURNSTILE NOTATION:
⊢ sign is called a “turnstile notation” and represents
one move.
⊢* sign represents a sequence of moves.
Eg- (p, b, T) ⊢ (q, w, α)
This implies that while taking a transition from state p to state
q, the input symbol ‘b’ is consumed, and the top of the stack
‘T’ is replaced by a new string ‘α’

18. Explanation : Initially, the state of automata is q0 and
symbol on stack is Z and the input is aaabbb as shown in
row 1. On reading ‘a’ (shown in bold in row 2), the state will
remain q0 and it will push symbol A on stack. On next ‘a’
(shown in row 3), it will push another symbol A on stack.
After reading 3 a’s, the stack will be AAAZ with A on the top.
After reading ‘b’ (as shown in row 5), it will pop A and move
to state q1 and stack will be AAZ. When all b’s are read, the
state will be q1 and stack will be Z. In row 8, on input
symbol ‘∈’ and Z on stack, it will pop Z and stack will be
empty. This type of acceptance is known as acceptance by
empty stack.

19. NOTE:
•The above pushdown automaton is deterministic in nature because there is only one
move from a state on an input symbol and stack symbol.
•The non-deterministic pushdown automata can have more than one move from a
state on an input symbol and stack symbol.
•It is not always possible to convert non-deterministic pushdown automata to
deterministic pushdown automata.
•Expressive Power of non-deterministic PDA is more as compared to expressive
deterministic PDA as some languages which are accepted by NPDA but not by
deterministic PDA which will be discussed in next article.
•The push down automata can either be implemented using accepetance by empty
stack or accepetance by final state and one can be converted to another.

20. 3)PARSE TREES

21. PARSE TREE:
•Parse tree is the hierarchical representation of
terminals or non-terminals.
•These symbols (terminals or non-terminals) represent
the derivation of the grammar to yield input strings.
•In parsing, the string springs using the beginning
symbol.
•The starting symbol of the grammar must be used as
the root of the Parse Tree.
•Leaves of parse tree represent terminals.
•Each interior node represents productions of grammar

22. RULES TO DRAW PARSE TREE:
1.All leaf nodes need to be terminals.
2.All interior nodes need to be non-terminals.
3.In-order traversal gives original input string..

26. USES OF PARSE TREE:
•It helps in making syntax analysis by reflecting the syntax of
the input language.
•It uses an in-memory representation of the input with a
structure that conforms to the grammar.
•The advantages of using parse trees rather than semantic
actions: you’ll make multiple passes over the info without
having to re-parse the input

27. THE END………