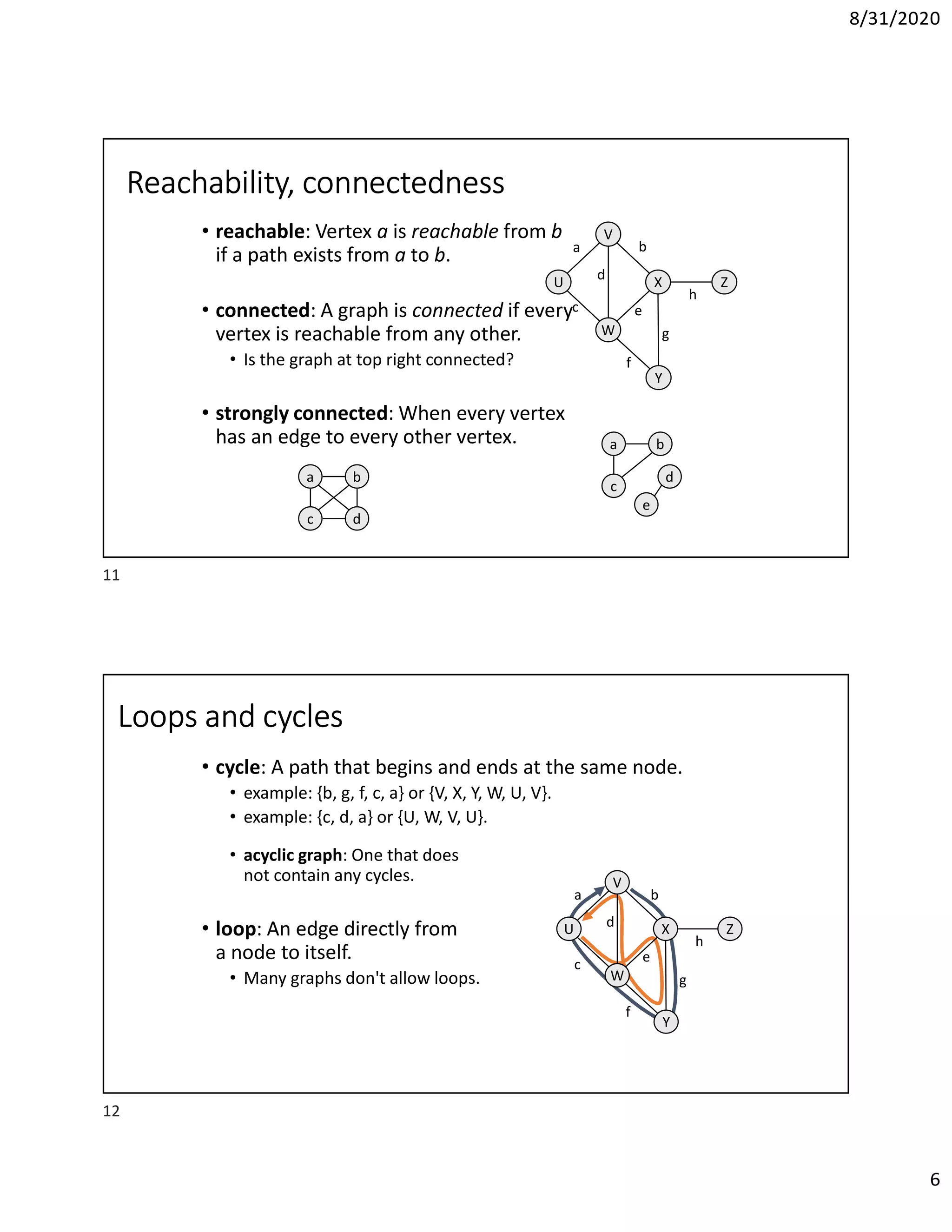
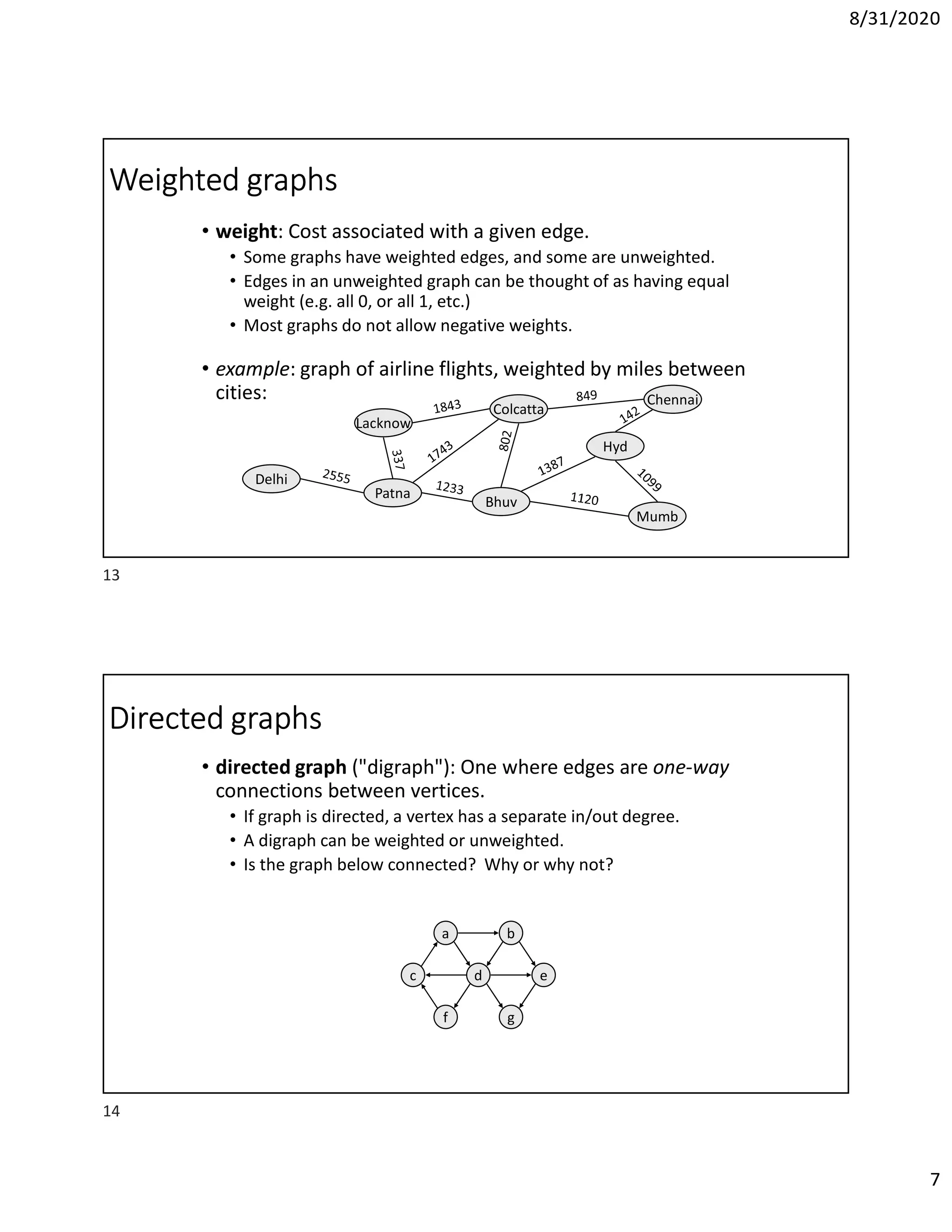
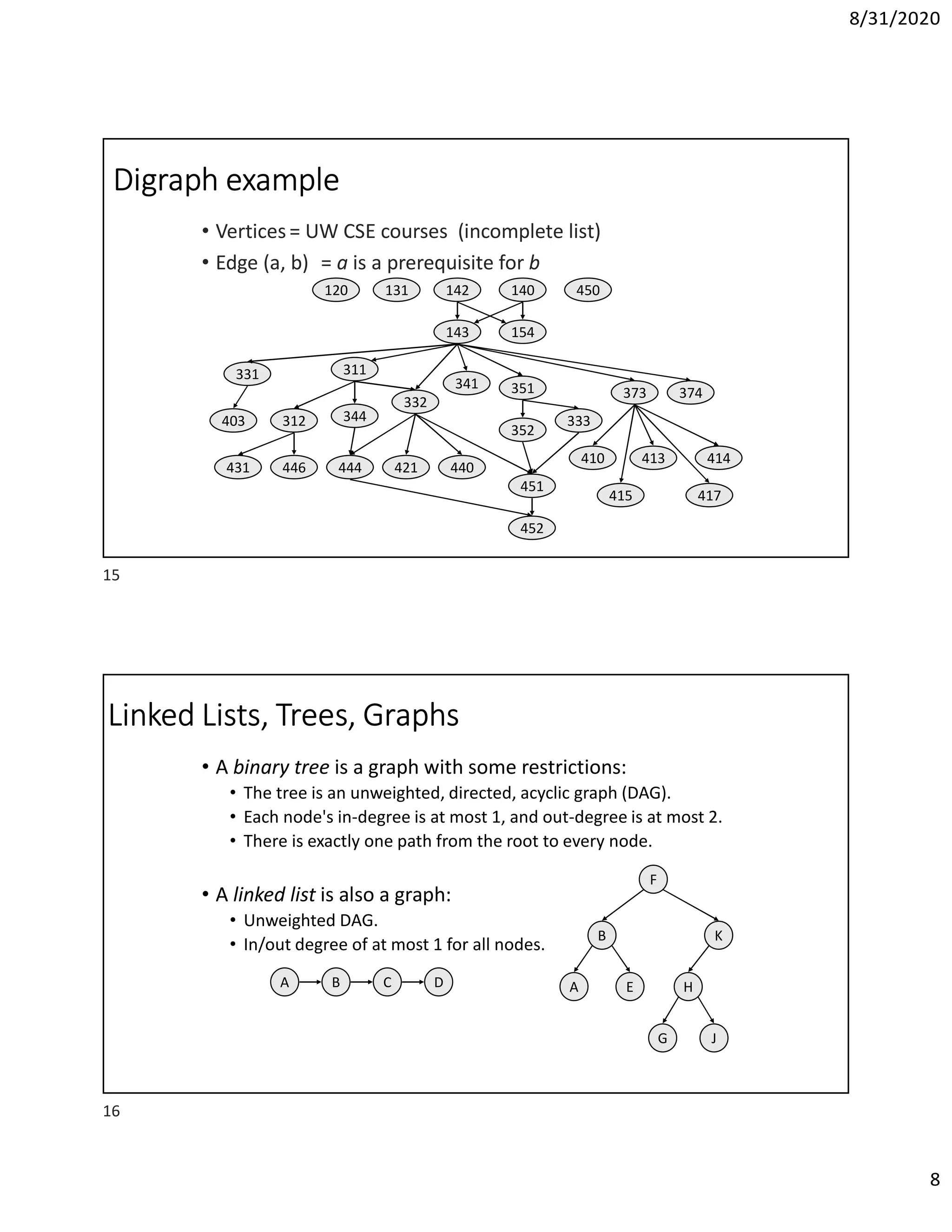
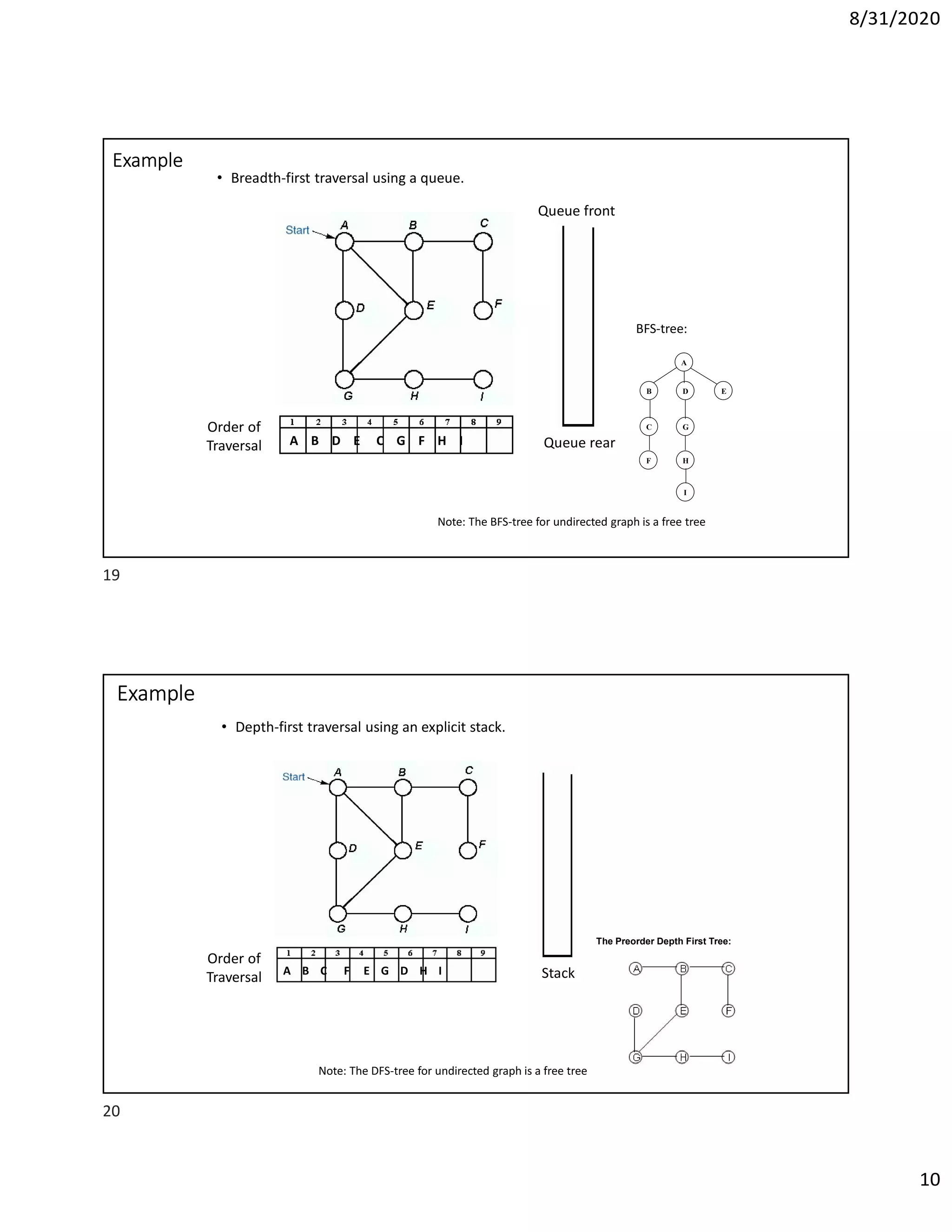
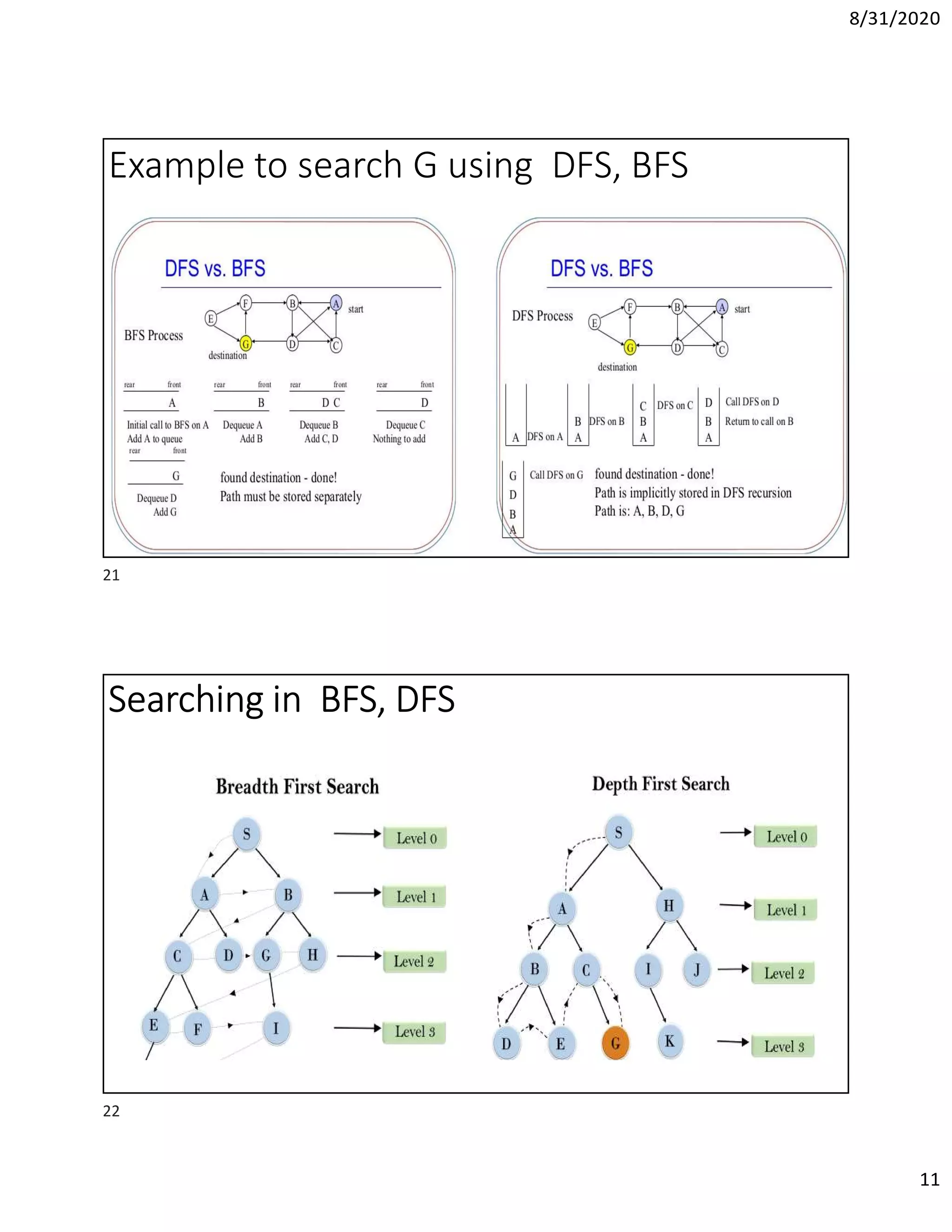
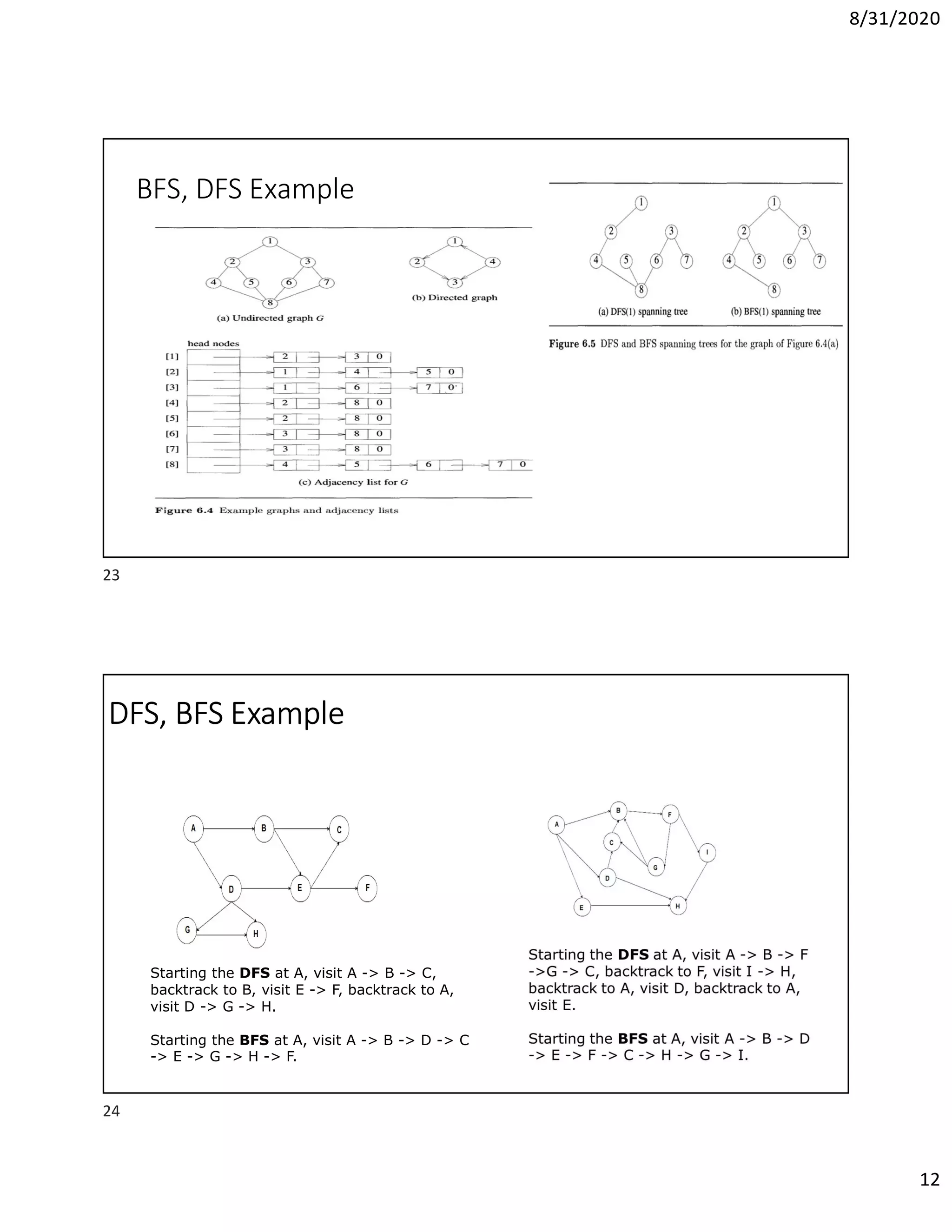
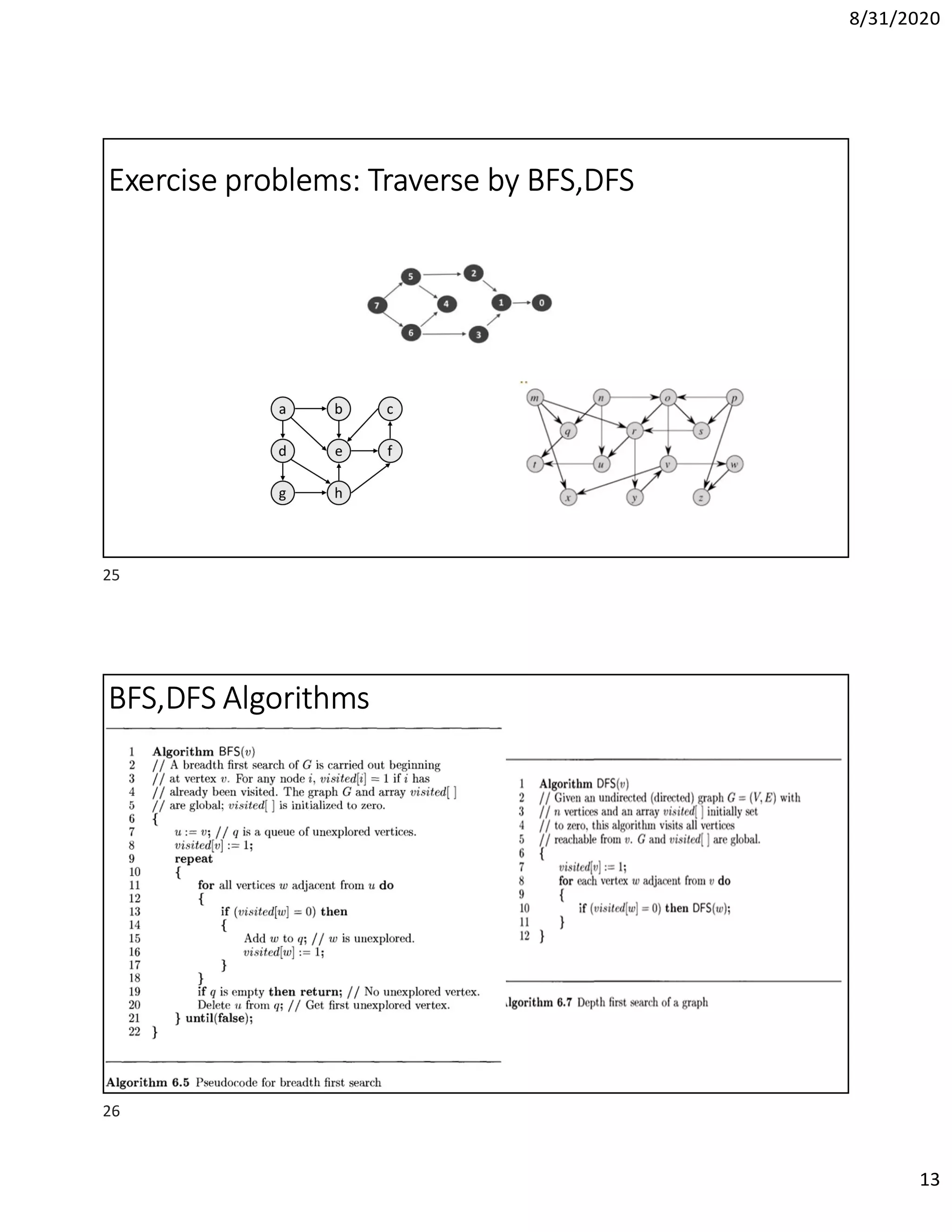
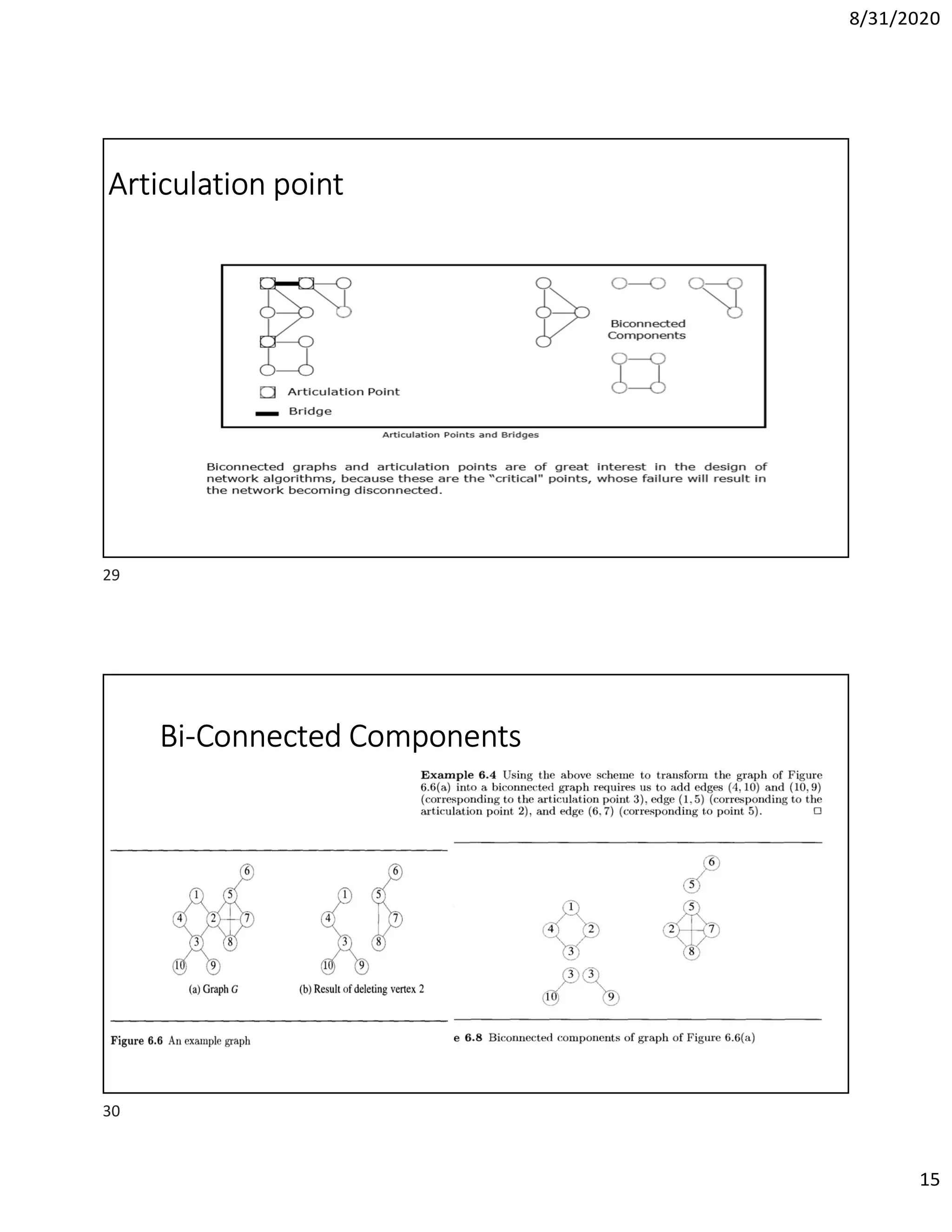
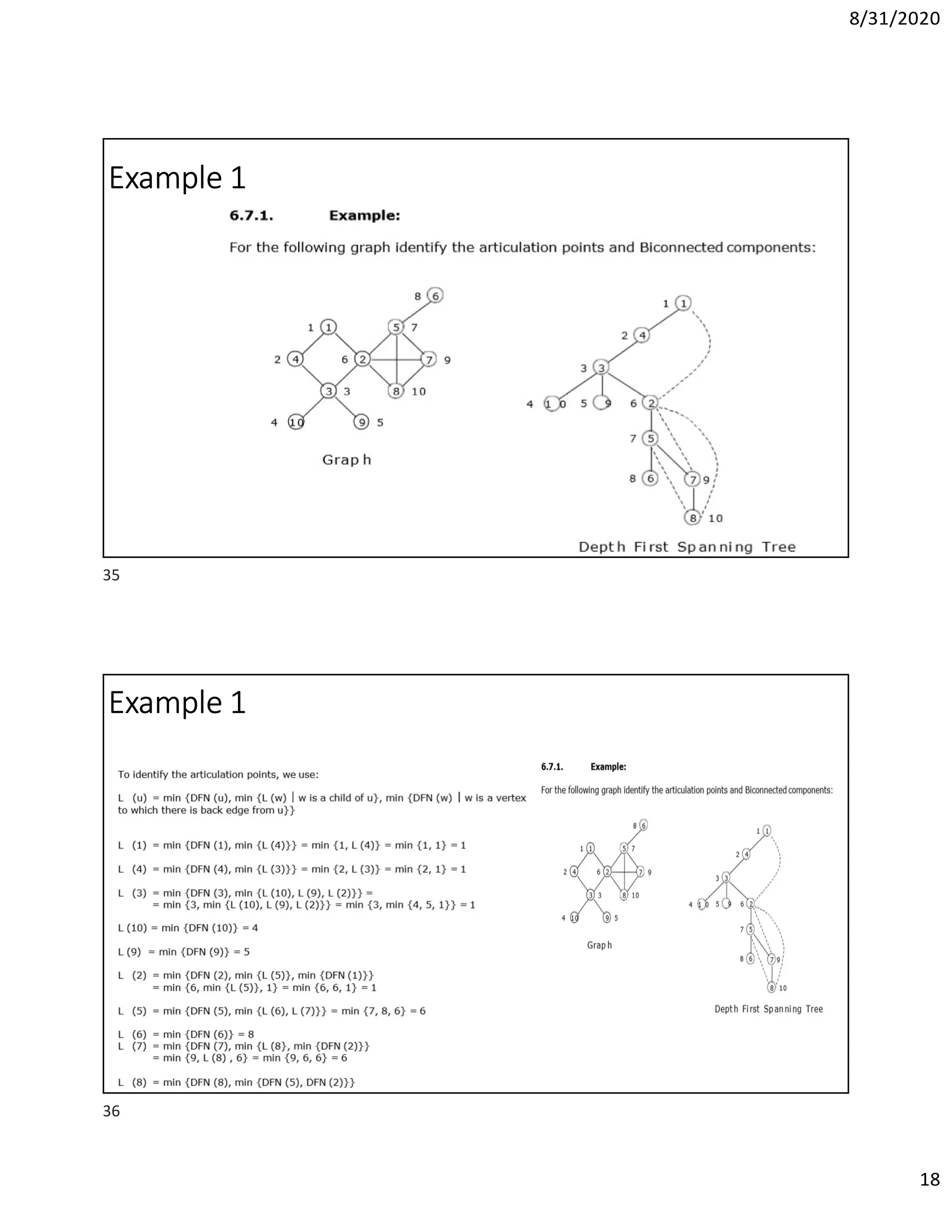
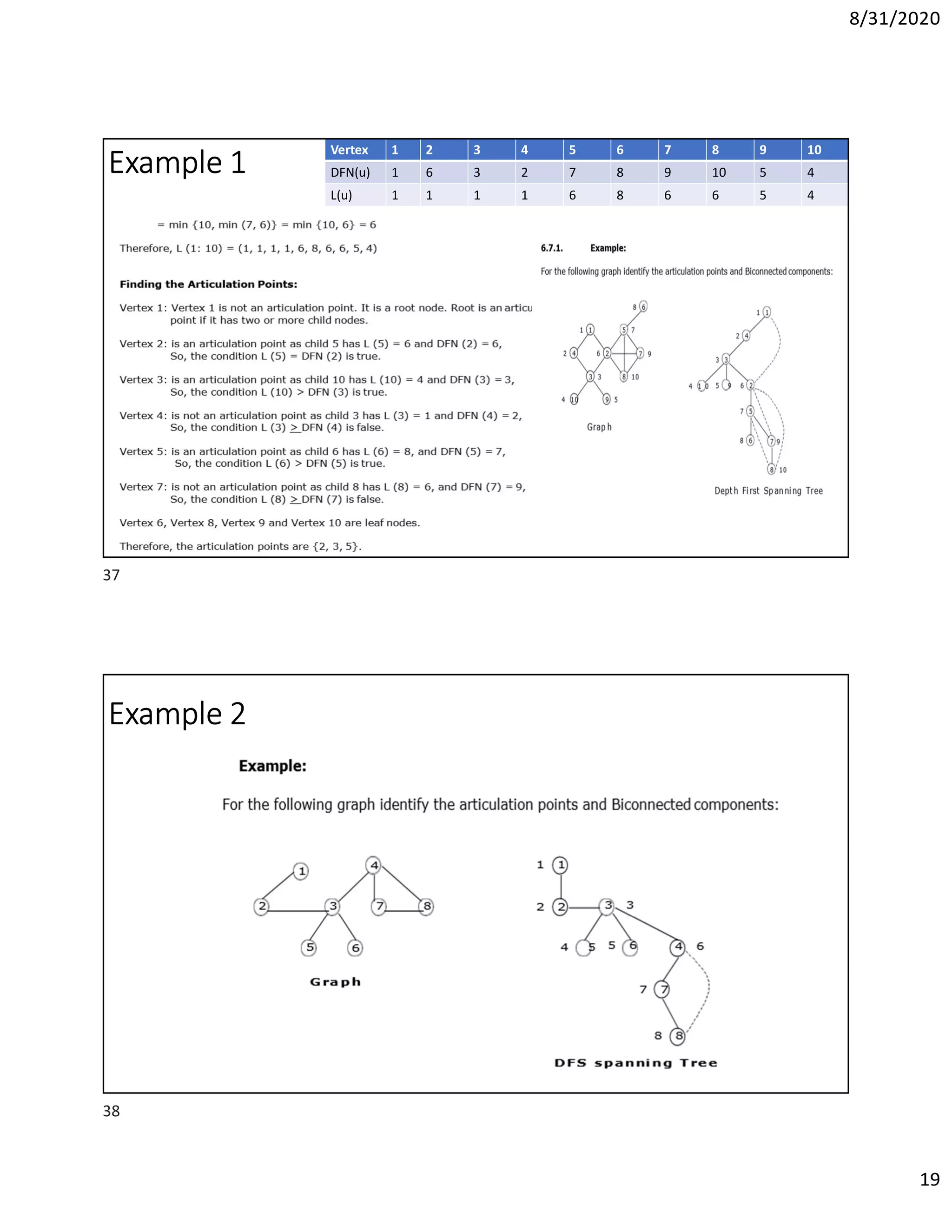
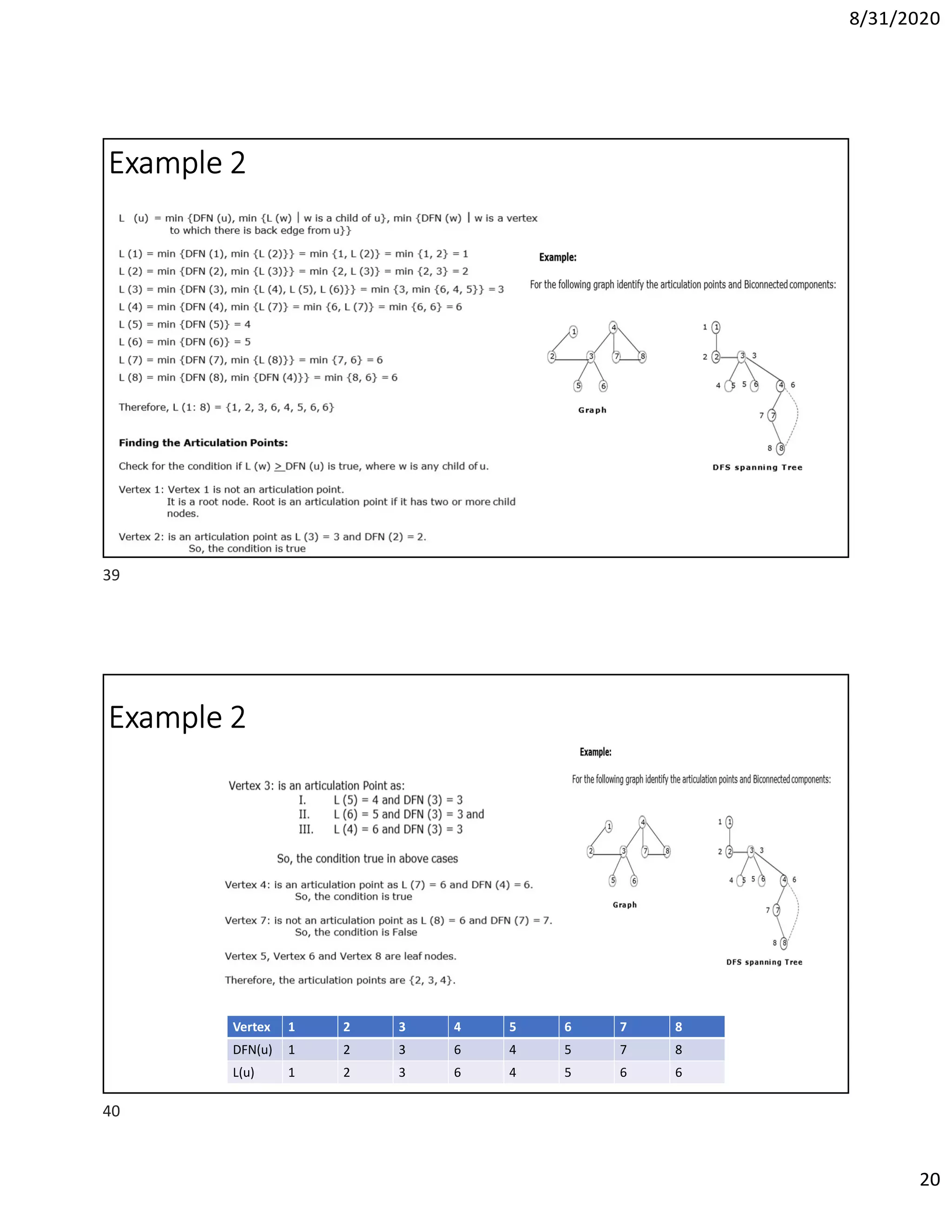
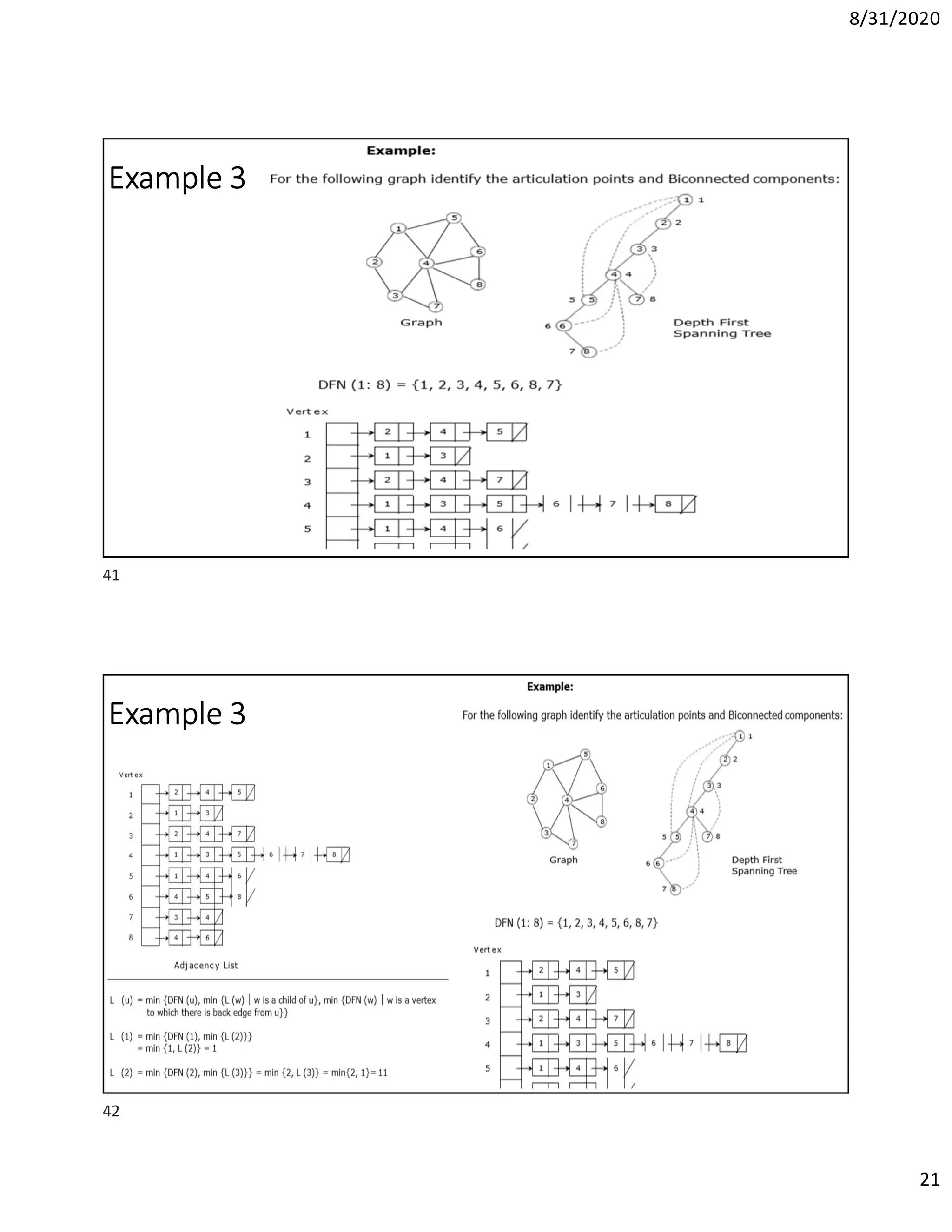
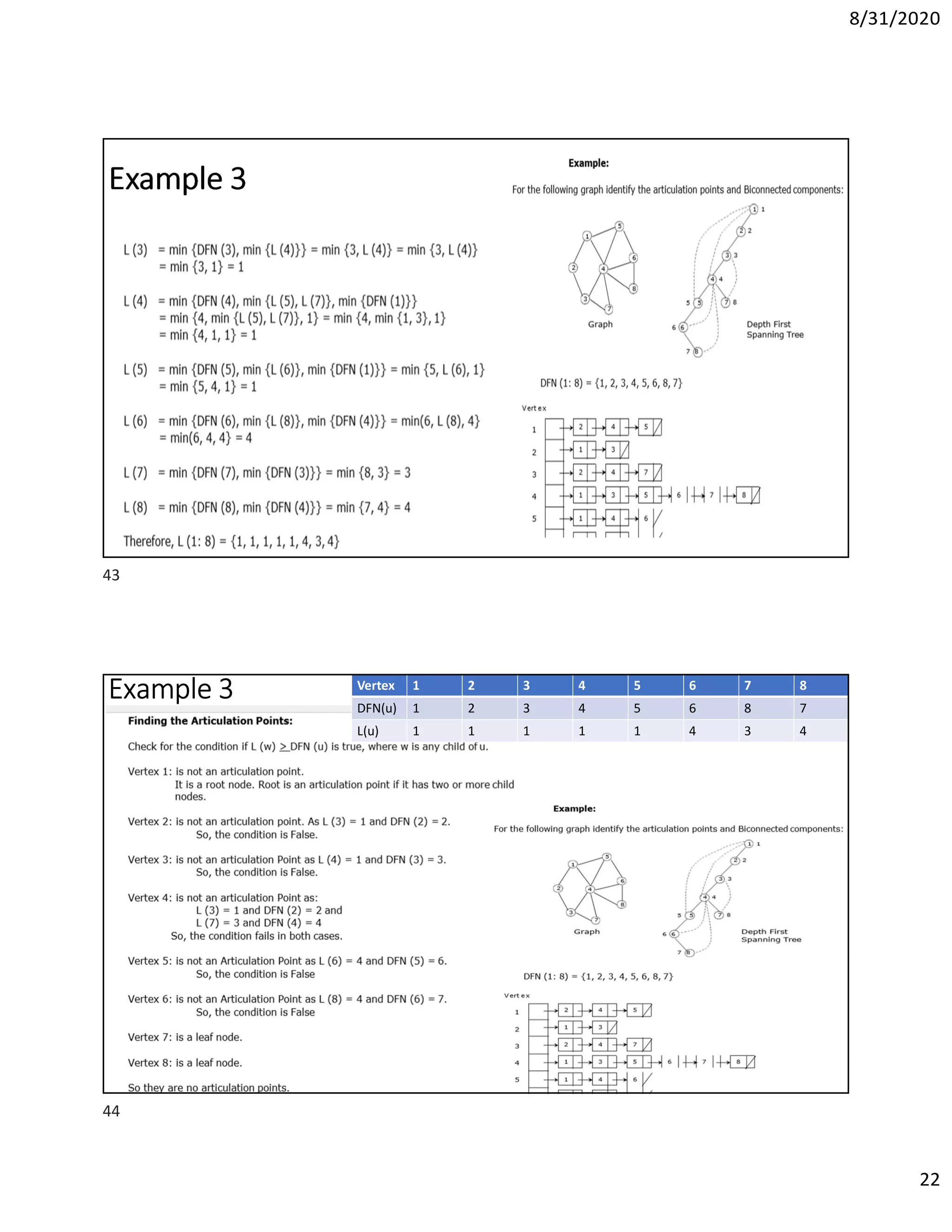
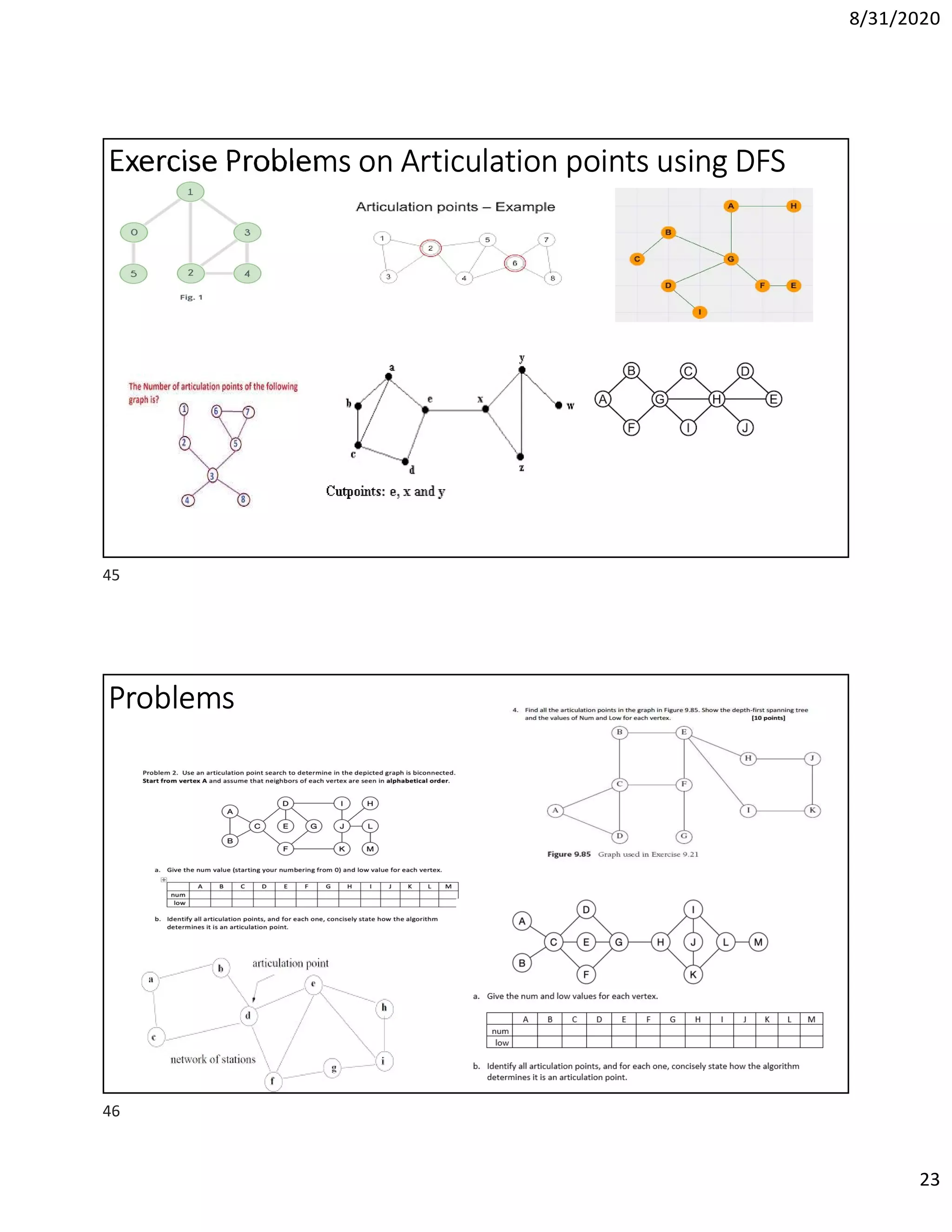
This document discusses algorithms for finding the maximum and minimum elements in an array, including the straightforward method that requires 2n-2 comparisons and the divide-and-conquer method that requires fewer comparisons. It also covers graph traversal algorithms like breadth-first search (BFS) and depth-first search (DFS), and discusses applications like finding articulation points in a graph. Examples of applying BFS, DFS, and the algorithm for finding articulation points using DFS are provided.

1. 8/31/2020
1
UNIT-II
• Max-Min Problem
• Graphs problems: BFS
• DFS
• Articulation point
Material prepared by Dr. N. Subhash Chandra
From Web resources, Computer Algorithms , Horowitz, Sahni &
Rajasekaran
Max-Min Problem
TWO METHODS:
• Method 1 Straight forward: if we apply the general approach to
the array of size n, the number of comparisons required are 2n-2.
• Method-2: Divide and Conquer approach: we will divide the
problem into sub-problems and find the max and min of each group,
now max of each group will compare with the only max of another
group and min with min.
Problem: Analyze the algorithm to find the
maximum and minimum element from an
array.
1
2

2. 8/31/2020
2
Straight forward Method: Max Min Problem
Divide Conquer method
Exercise problems: Construct Max-Min tree for
a) 25,13,8,50,98,-2,-17,45,55,88,97,5,-5
b) 78,-2,98,14,78,-10,67,45,39,100
3
4

3. 8/31/2020
3
Divide and Conquer Method Algorithm
Analysis of Divide and Conquer Method
5
6

4. 8/31/2020
4
Comparison of Straight forward method and
Divide and Conquer Method
Divide and Conquer the complexity 3n/2 – 2 is the best, average, worst case
number of comparison when n is a power of two.
Comparisons with Straight Forward Method:
Compared with the 2n – 2 comparisons for the Straight Forward method, this is a
saving of 25% in comparisons. It can be shown that no algorithm based on
comparisons uses less than 3n/2 – 2 comparisons.
Ex: n=8
Straight forward method: 2*8-2=14 comparisons
Divide and Conquer method: 3*8/2-2= 10 comparisons
Graph Traversal Algorithms
Traversing the graph means examining all the nodes and vertices of the
graph. There are two standard methods
• Breadth First Search
• Depth First Search
• Applications: Articulation point, Topological Sort, Convex hull
7
8

5. 8/31/2020
5
Graph Applications
• Web pages with links
• Road maps (e.g., Google maps)
• Airline routes
• Facebook friends
• Family trees
• Paths through a maze
Paths
• path: A path from vertex a to b is a sequence of edges that
can be followed starting from a to reach b.
• can be represented as vertices visited, or edges taken
• example, one path from V to Z: {b, h} or {V, X, Z}
• What are two paths from U to Y?
• path length: Number of vertices
or edges contained in the path.
• neighbor or adjacent: Two vertices
connected directly by an edge.
• example: V and X
XU
V
W
Z
Y
a
c
b
e
d
f
g
h
9
10

6. 8/31/2020
6
Reachability, connectedness
• reachable: Vertex a is reachable from b
if a path exists from a to b.
• connected: A graph is connected if every
vertex is reachable from any other.
• Is the graph at top right connected?
• strongly connected: When every vertex
has an edge to every other vertex.
XU
V
W
Z
Y
a
c
b
e
d
f
g
h
a
c
b
d
a
c
b
d
e
Loops and cycles
• cycle: A path that begins and ends at the same node.
• example: {b, g, f, c, a} or {V, X, Y, W, U, V}.
• example: {c, d, a} or {U, W, V, U}.
• acyclic graph: One that does
not contain any cycles.
• loop: An edge directly from
a node to itself.
• Many graphs don't allow loops.
XU
V
W
Z
Y
a
c
b
e
d
f
g
h
11
12

7. 8/31/2020
7
Weighted graphs
• weight: Cost associated with a given edge.
• Some graphs have weighted edges, and some are unweighted.
• Edges in an unweighted graph can be thought of as having equal
weight (e.g. all 0, or all 1, etc.)
• Most graphs do not allow negative weights.
• example: graph of airline flights, weighted by miles between
cities:
Colcatta
Chennai
Mumb
Bhuv
Lacknow
Patna
Hyd
Delhi
Directed graphs
• directed graph ("digraph"): One where edges are one-way
connections between vertices.
• If graph is directed, a vertex has a separate in/out degree.
• A digraph can be weighted or unweighted.
• Is the graph below connected? Why or why not?
a
d
b
e
gf
c
13
14

8. 8/31/2020
8
Digraph example
• Vertices= UW CSE courses (incomplete list)
• Edge (a, b) = a is a prerequisite for b
142
143 154
140
311
312
331
351
333
341
344403
352
373
120
410
332
374
131
421431 440
415
413
417
414
444446
450
451
452
Linked Lists, Trees, Graphs
• A binary tree is a graph with some restrictions:
• The tree is an unweighted, directed, acyclic graph (DAG).
• Each node's in-degree is at most 1, and out-degree is at most 2.
• There is exactly one path from the root to every node.
• A linked list is also a graph:
• Unweighted DAG.
• In/out degree of at most 1 for all nodes.
F
B
A E
K
H
JG
A B DC
15
16

9. 8/31/2020
9
Searching for paths
• Searching for a path from one vertex to another:
• Sometimes, we just want any path (or want to know there is a
path).
• Sometimes, we want to minimize path length (# of edges).
• Sometimes, we want to minimize path cost (sum of edge weights).
• What is the shortest path from MIA to SFO?
Which path has the minimum cost?
ORD
PVD
MIA
DFW
SFO
LAX
LGA
HNL
$500
Algorithms
Breadth First Search Depth First Search
• Visit start vertex and put into a FIFO
queue.
• Repeatedly remove a vertex from the
queue, visit its unvisited adjacent vertices,
put newly visited vertices into the queue.
17
18

10. 8/31/2020
10
Example
• Breadth-first traversal using a queue.
Order of
Traversal Queue rearA B D E C G F H I
Queue front
A
B D E
C G
F H
I
BFS-tree:
Note: The BFS-tree for undirected graph is a free tree
Example
• Depth-first traversal using an explicit stack.
Order of
Traversal StackA B C F E G D H I
The Preorder Depth First Tree:
Note: The DFS-tree for undirected graph is a free tree
19
20

11. 8/31/2020
11
Example to search G using DFS, BFS
Searching in BFS, DFS
21
22

12. 8/31/2020
12
BFS, DFS Example
DFS, BFS Example
Starting the DFS at A, visit A -> B -> C,
backtrack to B, visit E -> F, backtrack to A,
visit D -> G -> H.
Starting the BFS at A, visit A -> B -> D -> C
-> E -> G -> H -> F.
23
24

13. 8/31/2020
13
Exercise problems: Traverse by BFS,DFS
BFS,DFS Algorithms
25
26

14. 8/31/2020
14
Difference b/w DFS, BFS
Complexities: When a vertex is
removed from the queue, we
examine its adjacent vertices.
 O(n) if adjacency matrix used
 O(vertex degree) if adjacency
lists used
Total time
 O(mn), where m is number
of vertices in the component
that is searched (adjacency
matrix) = O(V2)
 Adjacency list =O(V+E)
Application of DFS: Articulation point
27
28

15. 8/31/2020
15
Articulation point
Bi-Connected Components
29
30

16. 8/31/2020
16
Algorithm for Bi-Connected graph
Finding Articulation point
31
32

17. 8/31/2020
17
Finding Articulation point using DFS
Finding Articulation point using DFS
33
34

18. 8/31/2020
18
Example 1
Example 1
35
36

19. 8/31/2020
19
Example 1
Vertex 1 2 3 4 5 6 7 8 9 10
DFN(u) 1 6 3 2 7 8 9 10 5 4
L(u) 1 1 1 1 6 8 6 6 5 4
Example 2
37
38

20. 8/31/2020
20
Example 2
Example 2
Vertex 1 2 3 4 5 6 7 8
DFN(u) 1 2 3 6 4 5 7 8
L(u) 1 2 3 6 4 5 6 6
39
40

21. 8/31/2020
21
Example 3
Example 3
41
42

22. 8/31/2020
22
Example 3
Example 3 Vertex 1 2 3 4 5 6 7 8
DFN(u) 1 2 3 4 5 6 8 7
L(u) 1 1 1 1 1 4 3 4
43
44

23. 8/31/2020
23
Exercise Problems on Articulation points using DFS
Problems
45
46

24. 8/31/2020
24
Algorithm for Articulation point
Time complexity of
above method is
O(V*(V+E)) for a
graph represented
using adjacency
list.
Algorithm to determine Bi-Connected Components
47
48