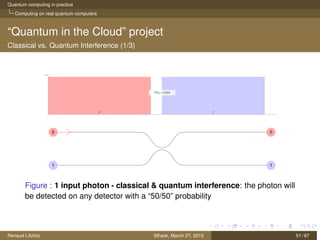
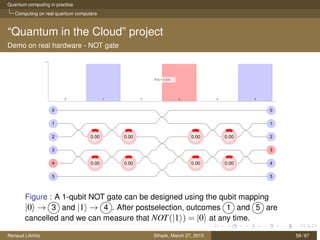
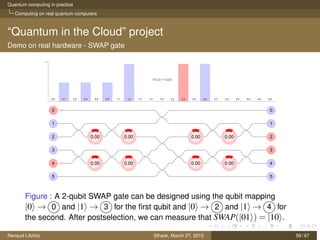
The document discusses quantum computing principles, quantum gates, fundamental algorithms, and their implications for cryptography. It covers essential aspects including quantum superposition, entanglement, and specific algorithms like Shor's and Grover's that challenge traditional cryptographic systems. Additionally, it provides insight into current quantum technologies and future directions in post-quantum cryptography.