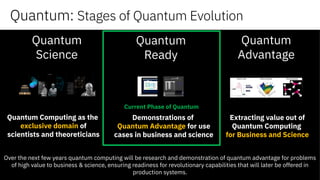
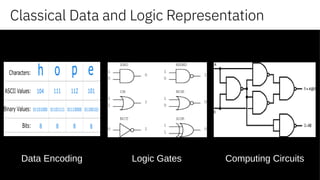
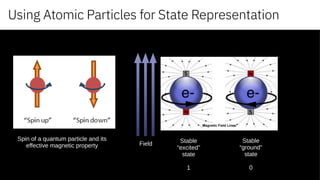
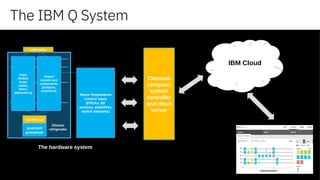
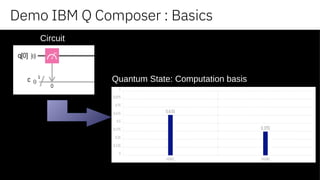
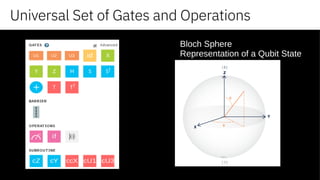
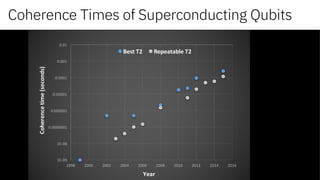
The document discusses the evolution and potential of quantum computing, highlighting its transition from a theoretical domain to practical applications in business and science. It explains key concepts such as superposition, coherence, and entanglement while showcasing quantum computing's advantages over classical computing for solving complex problems. Additionally, it outlines platforms and tools that enable developers to engage with quantum computing technology.

1. 1
Tim Ellison
Senior Technical Staff Member
IBM Hursley Laboratories
The Extraordinary
World of
Quantum
Computing

2. Courtesy of the Library of Congress

3. Classical Electronic Computing in its Infancy

4. Quantum: A New Form of Computing in its Infancy
1944
Colossus: the first electronic digital programmable
computer.
2015
IBM QX5Q: the first cloud quantum computing device

5. Quantum Computing as the
exclusive domain of
scientists and theoreticians
Quantum
Science
Demonstrations of
Quantum Advantage for use
cases in business and science
Quantum
Ready
Extracting value out of
Quantum Computing
for Business and Science
Quantum
Advantage
Reaction rates Reaction pathways Moleculegeometry
Over the next few years quantum computing will be research and demonstration of quantum advantage for problems
of high value to business & science, ensuring readiness for revolutionary capabilities that will later be offered in
production systems.
Current Phase of Quantum
Quantum: Stages of Quantum Evolution

7. Classical Computing

8. Classical Data and Logic Representation
Data Encoding Logic Gates Computing Circuits

9. Universal Turing Machine
1936

10. Classical Computer Resiliency
ECC
DRAM
Resilient Bit Store
Resilient
Data Representation
Resilient Algorithms

11. Hard problems for Classical Computers
Travelling Salesman
n cities = (n – 1)! / 2 options
10 cities ~= 1.8 million routes
20 cities ~= 1 billion billion routes
Optimizations
e.g. customer orders wood in various
lengths
Solution requires starting with a guess and
trying all options
Modelling Molecules
Simulate electron interactions
25 electrons ~= laptop sized problem
43 electrons ~= Titan supercomputer

12. General Hard Problem
80 20 8 73 65 54 39 74 30 4 93 67 79 77 12 10 38 51 88 50 56 5 ...
Find an element matching a value in an unordered set.
boolean found = element[x] == 74;
e.g. java.lang.String#indexof(char)
Best case:
Characters compared = 1
Worst case:
Characters compared = length
Average case:
Characters compared = length / 2

13. Enter Quantum Particles

14. Using Atomic Particles for State Representation
Stable
“excited”
state
1
Stable
“ground”
state
0
Field
Spin of a quantum particle and its
effective magnetic property

15. Quantum Mechanics: Superposition
Using external controls we can put the
particle into a spin phase that is both 0
and 1 in our measurement system.
When we observe the particle, it will
apparently collapse to either 0 or 1.
If there were an equal chance that it were
0 or 1 that would not be particularly
interesting, but we can influence the
probability of it being a 0 or 1.

16. Superposition and Quantum Randomness
We can put the quantum computer into a well-defined state that
gives us a random result when observed.
Is the system mostly pointing UP or DOWN?
50% of the time the answer is UP
50% of the time the answer is DOWN

17. Superposition and Quantum Randomness
We can put the quantum computer into a well-defined state that
gives us a random result when observed.
Is the system mostly pointing UP or DOWN?
50% of the time the answer is UP
50% of the time the answer is DOWN

18. Superposition and Quantum Randomness
We can put the quantum computer into a well-defined state that
gives us a random result when observed.
Is the system mostly pointing LEFT or RIGHT
100% of the time the answer is LEFT

19. Superposition and Quantum Randomness
We can put the quantum computer into a well-defined state that
gives us a random result when observed.
Is the system mostly pointing LEFT or RIGHT
50% of the time the answer is LEFT
50% of the time the answer is RIGHT

20. Entanglement: “Spooky action at a distance”
We can combine qubits to cause a correlation of these random
results when observed.
Is the system observed as 1 or 0
A: 50% of the time the answer is 1
50% of the time the answer is 0
B: Gives the same random answers
as qubit A
B
A
We can still perform deterministic operations on the two qubits.

21. The Power of Exponential Combination
Quantum computing power
comes from the ability to
combine qubits to represent
an exponentially increasing
set of values.

22. The Power of Exponential Combination
Quantum computing power
comes from the ability to
combine qubits to represent
an exponentially increasing
set of values.
One penny doubled every
31 days = $10,737,418.24

23. The Quantum Bit – “qubit”
Capture the effective
quantum particle
Its state is persistent
Stays set at 0 or 1
“coherence”
Apply energy to
control its state
Set to | 0 >
Set to | 1 >
Can observe its
current state

24. +
Chip with
superconducting
qubits and resonators
PCB with the qubit chip at
20mK
Protected from the
environment by multiple
shields
Microwave electronics
The Dilution Refrigerator

25. quantum
processor
connector
Input
Module
(coax
cables,
filters,
attenuators)
Output
module and
components
(isolators,
amplifiers)
Room Temperature
Control stack
(FPGAs, RF
sources, amplifiers,
switch networks)
connector
The hardware system
Dilution
refrigerator
Classical
computer
system
controller
and cloud
server
IBM Cloud
The IBM Q System

26. Demo IBM Q Composer : Basics
Circuit
Quantum State: Computation basis

27. Universal Set of Gates and Operations
Bloch Sphere
Representation of a Qubit State

28. Designing Quantum Algorithms
Quantum algorithms are often categorized by main techniques they employ, e.g. amplitude amplification,
quantum Fourier transform, phase kick-back, phase estimation, and quantum walk.

29. Qubits Coherence and Resilience

30. Coherence Times of Superconducting Qubits

31. Quantum
Volume
Number of qubits
(more is better)
Errors
(less is better)
Connectivity
(more is better)
Gate set
(more is better)
Performance of a Quantum Computer

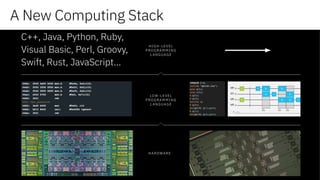
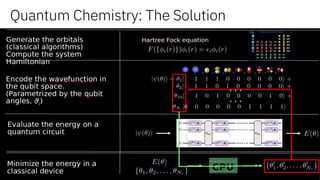
33. 33
reaction ratesmolecular structure
Sign problem: Monte-Carlo simulations of fermions are NP-hard [Troyer &Wiese, PRL 170201 (2015)]
Solving interacting fermionic problems is at the core of most challenges in computational
physics and high-performance computing:
What can quantum computers do?
Map fermions (electrons) to qubits and compute
First Demonstrations:
144 pauli terms, 36 sets
A. Kandala, et al. Nature 549 (2017)
Quantum Chemistry: The Problem

34. 34
Quantum Chemistry: The Solution

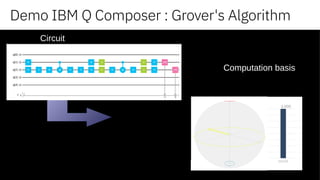
35. Grover's Algorithm
80 20 8 73 65 54 39 74 30 4 93 67 79 77 12 10 38 51 88 50 56 5 ...
Find an element matching a value in an unordered set.
boolean found = element[x] == 74;
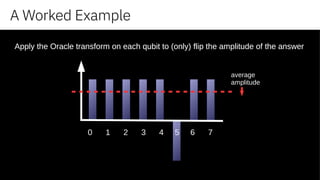
“oracle”
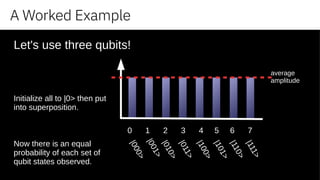
Revisit: search unordered set of values
Pseudo-code
- put qubits into superposition of all 2n states, with equal amplitude and equal probability,
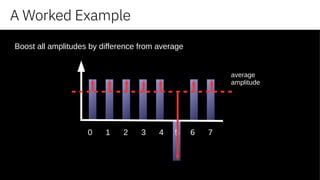
- amplify the answer based upon our “oracle” function,
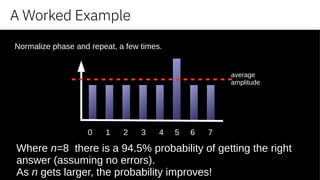
- expect the answer to form observed resulting state with highest probability.

36. A Worked Example
Let's use three qubits!
0 1 2 3 4 5 6 7
average
amplitude
|000>
|001>
|010>
|011>
|100>
|101>
|110>
|111>
Now there is an equal
probability of each set of
qubit states observed.
Initialize all to |0> then put
into superposition.

37. A Worked Example
Apply the Oracle transform on each qubit to (only) flip the amplitude of the answer
0 1 2 3 4 5 6 7
average
amplitude
Apply the Oracle transform on each qubit to (only) flip the amplitude of the answer

38. A Worked Example
Boost all amplitudes by difference from average
0 1 2 3 4 5 6 7
average
amplitude

39. A Worked Example
Normalize phase and repeat, a few times.
0 1 2 3 4 5 6 7
average
amplitude
Where n=8 there is a 94.5% probability of getting the right
answer (assuming no errors).
As n gets larger, the probability improves!

40. Demo IBM Q Composer : Grover's Algorithm
Circuit
Sphere Computation basis

41. Factoring
881 x 409 = 360329 easy
360329 = 881 x 409 hard
RSA cryptography depends upon this property, e.g. when
publishing a public key.
Best classical solution Number Field Sieve is O(exp(c.b1/3)
)

42. Factoring

43. A New Computing Stack

44. Demo: Tools for Developers

45. Since Launch
• > 50,000 users
• > 500,000 executions
• 20 scientific
publications
IBM Q Experience
• Simulation
• Graphical
programming
• QASM language
• API & SDK
• Active user
community
IBM Q Experience: World’s First Public Quantum Computer and Developer Ecosystem
Quantum Computing for Everyone