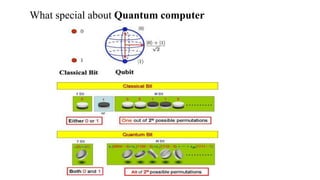
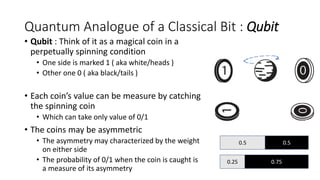
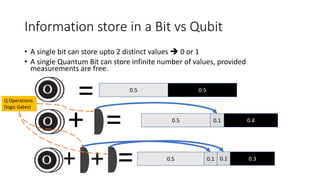
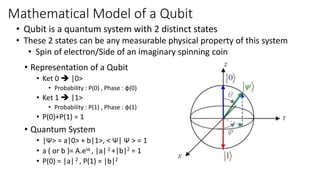
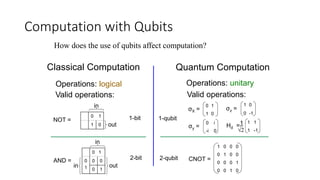
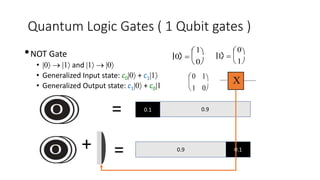
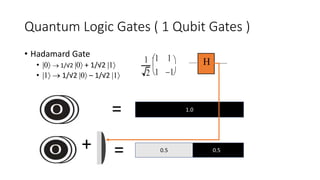
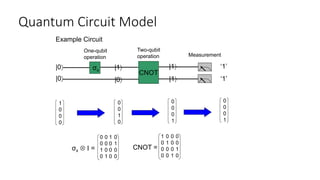
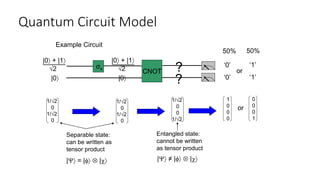
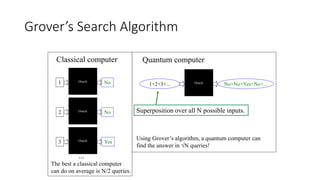
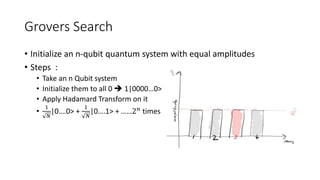
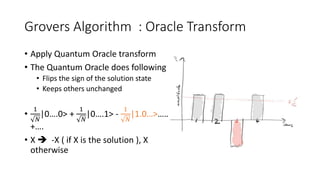
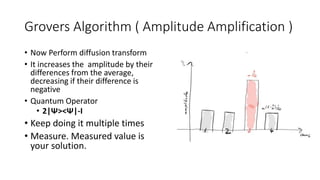
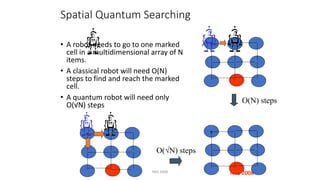
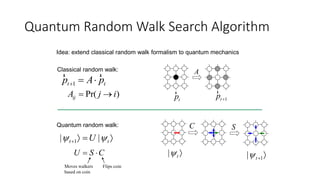
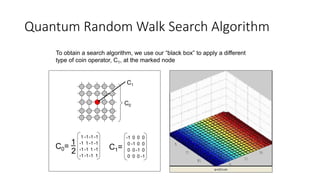
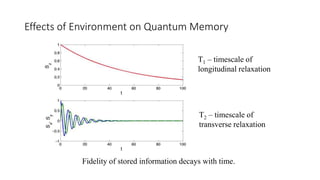
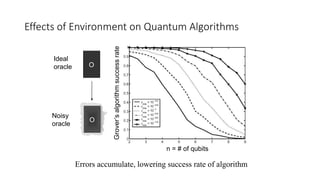
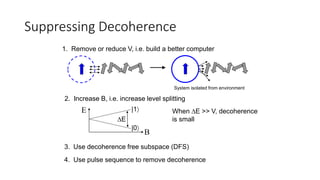
The document discusses quantum computation, including its principles and historical development, starting from Richard Feynman's proposal in 1982 to the advancements made by David Deutsch and Peter Shor. It compares classical and quantum computing, explaining concepts like qubits, quantum gates, algorithms, and applications in fields such as cryptography and artificial intelligence. The document highlights the potential of quantum computers to perform complex calculations more efficiently than classical computers due to their unique properties, including superposition and entanglement.

1. Quantum Computation
Prasenjit
Principal Engineering Manager@Microsoft

2. Nobody understands quantum
mechanics
“No, you’re not going to be able to understand it. . . .
You see, my physics students don’t understand it
either. That is because I don’t understand it. Nobody
does. ... The theory of quantum electrodynamics
describes Nature as absurd from the point of view of
common sense. And it agrees fully with an
experiment. So I hope that you can accept Nature as
She is -- absurd.”
Richard Feynman
Absurd : Yes, but works perfect as per those very
absurd equations and laws which governs them!!!

3. Agenda
• Introduction to Quantum Computation
• Brief History and Need of Quantum Computing
• Quantum Computing concepts
• Comparison with Classical Computing
• Qubits
• Quantum Logic Gates
• Quantum Circuits
• Quantum Programming
• Quantum Hello World
• Quantum Algorithms

4. History
 1982 - Feynman proposed the idea of creating
machines based on the laws of quantum
mechanics instead of the laws of classical
physics.
 1985 - David Deutsch developed the quantum
Turing machine, showing that quantum circuits
are universal.
 1994 - Peter Shor came up with a quantum
algorithm to factor very large numbers in
polynomial time.
 1997 - Lov Grover develops a quantum search
algorithm with O(√N) complexity

5. Why quantum computer
 Moore’ law slowing down in 2020
it is flattened out.
 Classical computers are based on
ON/OFF switches used to form Logic
Gates which are called transistors.
 Smaller transistors  Increased
portable computing power
 But transistor cannot be made
smaller due to the laws of Quantum
Mechanics starts to take over.
 At atomic scale (<1nm ) electrons
pass through closed logic gates ( aka
OFF switches ) due to Quantum
Tunneling, which nullifies presence
of Logical switches.
 This breaks the classical
computation paradigm and holds
us back from increasing the
computation power of our
Computers.

6. APPLICATIONS
• Cryptography
• Artificial intelligence
• Quantum Processing
• Quantum Search
• Quantum communication
• Teleportation

7. What is a Quantum Computer
A quantum computer is a machine that performs calculations based on
the laws of quantum mechanics, which is the behavior of particles at
the sub-atomic level.
Basic concepts of a classical computer and its Quantum analogues :
• Data Representation  Bits/Bytes Qubits
• Data Computation  Logic Gates  Quantum Gates
• Data Observation  Read Bits/Bytes Q Measurments
• Algorithms  Lookup/Search  Q Algos

8. What special about Quantum computer

9. Data Representation : The Bit
The basic component of a classical computer is the bit, a single
binary variable of value 0 or 1.
1
0
0
1
The state of a classical computer is described by some
long bit string of 0s and 1s.
0001010110110101000100110101110110...
At any given time, the value
of a bit is either ‘0’ or ‘1’.

10. Quantum Analogue of a Classical Bit : Qubit
• Qubit : Think of it as a magical coin in a
perpetually spinning condition
• One side is marked 1 ( aka white/heads )
• Other one 0 ( aka black/tails )
• Each coin’s value can be measure by catching
the spinning coin
• Which can take only value of 0/1
• The coins may be asymmetric
• The asymmetry may characterized by the weight
on either side
• The probability of 0/1 when the coin is caught is
a measure of its asymmetry
0.50.5
0.750.25

11. Information store in a Bit vs Qubit
• A single bit can store upto 2 distinct values  0 or 1
• A single Quantum Bit can store infinite number of values, provided
measurements are free.
0.1 0.40.5
+ =
+ 0.10.5
+ = 0.1
= 0.5 0.5
0.3
Q Operations
(logic Gates)

12. Mathematical Model of a Qubit
• Representation of a Qubit
• Ket 0  |0>
• Probability : P(0) , Phase : ɸ(0)
• Ket 1  |1>
• Probability : P(1) , Phase : ɸ(1)
• P(0)+P(1) = 1
• Quantum System
• |Ψ> = a|0> + b|1>, < Ψ| Ψ > = 1
• a ( or b )= A.eiα , |a|2 +|b|2 = 1
• P(0) = |a|2 , P(1) = |b|2
• Qubit is a quantum system with 2 distinct states
• These 2 states can be any measurable physical property of this system
• Spin of electron/Side of an imaginary spinning coin

13. The Qubit
A quantum bit, or qubit, is a two-state system which
obeys the laws of quantum mechanics.
=|1 =|0
Valid qubit states:
| = |0
| = |1
| = (|0- ei/4 |1)/2
| = (2|0- 3ei5/6 |1)/13
Spin-½ particle
The state of a qubit | can be thought of as a vector in
a two-dimensional Hilbert Space, H2, spanned by the
Basis vectors |0 and |1.

14. Data Computation : on Bits/Qubits
How does the use of qubits affect computation?
Classical Computation
Data unit: bit
x = 0 x = 1
0
1
0
1
Valid states:
x = ‘0’ or ‘1’ | = c1|0 + c2|1
Quantum Computation
Data unit: qubit
Valid states:
| = |0 | = |1 | = (|0 + |1)/√2
=|1 =|0= ‘1’ = ‘0’

15. Computation with Qubits
0 1
1 0
How does the use of qubits affect computation?
Classical Computation
Operations: logical
Valid operations:
AND =
0 i
-i 0
1 0
0 -1
1 1
1 -1
0 1
0
1
0 0
0 1
NOT =
0 1
1 0
in
out
out
in
in
1 0 0 0
0 1 0 0
0 0 0 1
0 0 1 0
1-bit
2-bit
Quantum Computation
Operations: unitary
Valid operations:
σX =
σy =
σz =
Hd =
CNOT =
√2
1
1-qubit
2-qubit

16. Computation with Qubits
How does the use of qubits affect computation?
Classical Computation
Measurement: deterministic
x = ‘0’
State Result of measurement
‘0’
x = ‘1’ ‘1’
Quantum Computation
Measurement: stochastic
| = |0
| = |0- |1
State Result of measurement
| = |1
2
‘0’
‘1’
‘0’ 50%
‘1’ 50%

17. More than one qubit
1
0
0
0
u11 u12
u21u22
Single qubit
c1
c2
c1
c2
Two qubits
H2 =
1
0
0
1,
|0,|1
H2
2 = H2H2 = ,
|00,|01,|10,|11
0
1
0
0
,
0
0
1
0
,
0
0
0
1
c1
c2
c3
c4
c1
c2
c3
c4
u11 u12 u13 u14
u21 u22 u23 u24
u31 u32 u33 u34
u41 u42 u43 u44
Hilbert
space
U| = U| =Operator
| = c1|0 + c2|1 = |
c1|00 + c2|01 +
c3|10 + c4|11
==
Arbitrary
state

18. Quantum Logic Gates ( 1 Qubit gates )
•NOT Gate
• |0  |1 and |1  |0
• Generalized Input state: c0|0 + c1|1
• Generalized Output state: c1|0 + c0|1
X0 1
1 0


 

0.1
= 0.9
+ = 0.9 0.1
0 
1
0


 

1 
0
1


 


19. Quantum Logic Gates ( 1 Qubit Gates )
• Hadamard Gate
• |0  1/√2 |0 + 1/√2 |1
• |1  1/√2 |0 – 1/√2 |1
1
2
1 1
1 1


 

H
1.0
=
0.50.5+ =

20. Advanced Computer Architecture Laboratory
• Controlled NOT (CNOT)
• Flips second Qubit iff the Control Qubit=1
• Quantum generalization of XOR Gate
• Input : a|00>+b|01>+c|10>+d|11>
• Output : a|00>+b|01>+d|10>+c|11>
• Specific Example :
• Let Qubit 1  a|0>+c|1>
• Let Qubit 2  |0>
• Input : a|00>+0|01>+ c|10>+0|11>
• Output : a|00>+0|01>+0|10>+c|11>
Quantum Gates ( 2 Qubit Gates)
1 0 0 0
0 1 0 0
0 0 0 1
0 0 1 0











21. Quantum Entanglement
• Einstein never believed it and called it “Spooky Action At Distance”
• Though recent experiments have verified the properties of
Entanglement ( Famous EPR Paradox )
• Quantum mechanics allows “entangled states” of 2 distant systems
• Measuring property of One system can instantly change property of
the other entangled system, even if they are light years apart.
• Breaks law of causality and can have information travel more than
c(?)

22. Quantum Entanglement
• Entangled Quantum systems requires following :
• Create a 2-qubit system
• Entangle them by some Quantum Operation
• Give 1 qubit to Bob and another to Alice
• Bob only needs to measure his Qubit to know value of Alice’s Qubit
• Recall our previous CNOT Example
• Input  qubit1: a|0>+c|1>, qubit2 : |0>
• Output  Superposed quantum enatangled 2-qubit State : a|00>+c|11>
• Uses of Quantum Entanglement
• Quantum Teleportation ( Quantum Internet ), SuperDense Coding, ClockSync

23. Quantum Circuit Model
1
0
0
0
0 0 1 0
0 0 0 1
1 0 0 0
0 1 0 0
σx  I =
0
0
1
0
1 0 0 0
0 1 0 0
0 0 0 1
0 0 1 0
CNOT =
0
0
0
1
0
0
0
1
|0
|0
|1
|0
|1
|1
‘1’
‘1’
Example Circuit
σx
One-qubit
operation
CNOT
Two-qubit
operation Measurement

24. Quantum Circuit Model
1/√2
0
1/√2
0
1
0
0
0
σx
CNOT
|0 + |1
|0
Example Circuit
√2
______
1/√2
0
1/√2
0
1/√2
0
0
1/√2
0
0
0
1
|0 + |1
|0
√2
______
‘0’
‘0’
or
‘1’
‘1’
or
50% 50%
Separable state:
can be written as
tensor product
| = |  |
Entangled state:
cannot be written
as tensor product
| ≠ |  |
?
?

25. Quantum Algorithms
• Grover’s search algorithm
• Approximate Quantum Fourier Transforms
• Quantum random walk search algorithm
• Shor’s Factoring Algorithm

26. Application of Grovers Search Algorithm
• Grover’s algorithm can identify an item from a list of N elements in
• What’s this good for?
• Unstructured database search (virtual database)
• Search an usorted list
• breaking DES (Data Encryption Standard)
• SAT (Satisfyability of boolean formula)
• map coloring with 4 colors
 NO

27. Grover’s Search Algorithm
The best a classical computer
can do on average is N/2 queries.
1 Oracle
No
...
2 Oracle
No
3 Oracle
Yes
Classical computer
Oracle
1+2+3+... No+No+Yes+No+...
Quantum computer
Using Grover’s algorithm, a quantum computer can
find the answer in N queries!
Superposition over all N possible inputs.

28. Grovers Search
• Suppose you are given a large list of items. Among these items there
is one item with a unique property that we wish to locate; we will call
this one the winner . Think of each item in the list as a box of a
particular color. Say all items in the list are gray except the winner ,
which is pink.
• Classical Algorithm requires (N+1)/2 on an average

29. Grovers Search
• Initialize an n-qubit quantum system with equal amplitudes
• Steps :
• Take an n Qubit system
• Initialize them to all 0  1|0000…0>
• Apply Hadamard Transform on it
•
1
𝑁
|0….0> +
1
𝑁
|0….1> + ……2 𝑛 times

30. Grovers Algorithm : Oracle Transform
• Apply Quantum Oracle transform
• The Quantum Oracle does following
• Flips the sign of the solution state
• Keeps others unchanged
•
1
𝑁
|0….0> +
1
𝑁
|0….1> -
1
𝑁
|1.0…>……
+….
• X  -X ( if X is the solution ), X
otherwise

31. Grovers Algorithm ( Amplitude Amplification )
• Now Perform diffusion transform
• It increases the amplitude by their
differences from the average,
decreasing if their difference is
negative
• Quantum Operator
• 2|Ψ><Ψ|-I
• Keep doing it multiple times
• Measure. Measured value is
your solution.

32. Grover’s Search Algorithm
Pros:
Can be used on any unstructured search problem, even
NP-complete problems.
Cons:
Only a quadratic speed-up over classical search.
O
σz
O
σz
…
…
…
…
|0
|0
|0
O(N) iterations
Hd
Hd
Hd
…Hd
Hd
Hd
…
Hd
Hd
Hd
…
Hd
Hd
Hd
…
Hd
Hd
Hd

33. NKS 2008
Does biological computation use quantum
searching?
• Mystery – DNA computation in cells uses an alphabet
of size 4 and protein synthesis uses an alphabet of
size 20 (20 amino acids).
• Observation – (Apoorva Patel, 2000) – Quantum
searching is most efficient when carried out for
databases of size:
4 - (requires 1 query)
10 - (requires 2 queries)
20 – ( requires 3 queries)

34. NKS 2008
h
Spatial Quantum Searching
• Quantum search type
algorithms can be used to
search a distributed
database using only
neighbor to neighbor
communications.with a
square-root speedup
over a classical database.
(Aaronson 2001)

35. Spatial Quantum Searching
• A robot needs to go to one marked
cell in a multidimensional array of N
items.
• A classical robot will need O(N)
steps to find and reach the marked
cell.
• A quantum robot will need only
O(√N) steps
NKS 2008
h
NKS 2008
h
ONsteps
h
O√Nsteps

36. NKS 2008
Photosynthesis
• Photosynthesis in plants is extremely efficient – unlike other chemical
& biological reactions, it is able to transport almost 100% of the
photons to the desired locations.
• This used to be a mystery – one possible explanation was given by
Fleming et al (Nature – April 14, 2007) where they analyzed the way
the energy flows in the cells as a spatial quantum search problem.

37. Does Nature use Quantum Searching?
Original algorithm - Database search & function inversion
Applications:
• Collision problem & Element Distinctness
• Communication algorithms
• Precision Measurements
• Pendulum Modes
Natural applications
• Genetic Pattern Matching (??)
• Photosynthesis (??)

38. Quantum Random Walk Search Algorithm
Idea: extend classical random walk formalism to quantum mechanics
A
tp
r
1tp 
r
Classical random walk:
C S
| t  1| t  
Quantum random walk:
1| |t tU    
U S C 
Moves walkers
based on coin
Flips coin
Pr( )ijA j i 
1t tp A p  
r r

39. Quantum Random Walk Search Algorithm
To obtain a search algorithm, we use our “black box” to apply a different
type of coin operator, C1, at the marked node
C0
C1
1 -1-1 -1
-1 1 -1 -1
-1 -1 1 -1
-1 -1-1 1
C0=
1
2
C1=
-1 0 0 0
0 -1 0 0
0 0 -1 0
0 0 0 -1

40. Quantum Random Walk Search Algorithm
Pros:
As general as Grover’s search algorithm.
Cons:
Same complexity as Grover’s search algorithm.
Slightly more complicated in implementation
Slightly more memory used
Interesting Feature: Search algorithm flows naturally
out of random walk formalism. Motivation for new QRW-
based algorithms?

41. Quantum Hello World

42. Quantum Hello World
• https://docs.microsoft.com/en-us/quantum/quantum-
installconfig?view=qsharp-preview

43. Q & A

44. Appendix

45. Decoherence and Noise
What happens to a qubit when it interacts with an environment?
0
0 1,
1
z
j j
j
H H V
H B
V A

 
 

 
r r
Quantum computer Environment
V
Quantum information is lost through decoherence.
σ1
σ2 σ3
σN…

46. Types of Decoherence
T1 processes: longitudinal relaxation, energy is lost to the environment
V
T2 processes: transverse relaxation, system becomes entangled with
the environment
V
+
+
What are the effects of decoherence?

47. Effects of Environment on Quantum Memory
Fidelity of stored information decays with time.
T1 – timescale of
longitudinal relaxation
T2 – timescale of
transverse relaxation

48. Effects of Environment on Quantum Algorithms
Errors accumulate, lowering success rate of algorithm
Grover’salgorithmsuccessrate
n = # of qubits
O
O
Ideal
oracle
Noisy
oracle

49. Suppressing Decoherence
1. Remove or reduce V, i.e. build a better computer
System isolated from environment
2. Increase B, i.e. increase level splitting
B
E
|0
|1 When E >> V, decoherence
is smallE
3. Use decoherence free subspace (DFS)
4. Use pulse sequence to remove decoherence